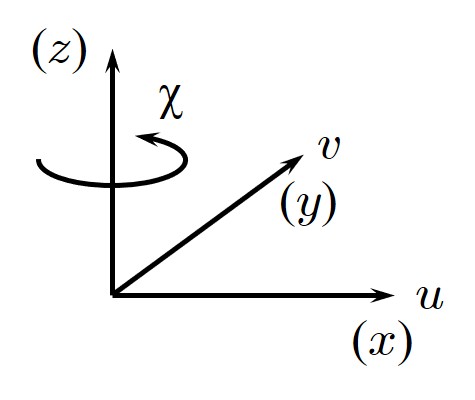地盤構造物に対する安定解析、例えば、地盤の変形や沈下、応力分布、支持力、斜面安定、土圧などの解析は設計、施工上非常に重要な課題であり、古くから弾性学や剛塑性理論を基礎として研究されてきた。しかし、この種の問題は数学的に極めて複雑な
非線形境界値問題となるため、解析的に解き得る場合は局限され、多かれ少なかれ数値解析手法によって近似解を求めざるを得ないのが現状である。
一方、航空機技術者によって開発され、電子計算機の発達に伴い驚異的に進歩を遂げてきた
有限要素法は、今日、構造解析の手法として不動の地位を確保するに至った。近年、有限要素法は構造解析に対する利用に限定されることなく、流体解析や地盤の応力解析など、幅広い分野においても利用されるようになってきた｡
ところで、土や岩盤の破壊を議論する場合、
図1.1 に示されるように微視的立場と巨視的立場の二通りが考えられる。微視的立場からは材料の性質を調べる研究が行われている。通常の応力解析は一般的に後者の巨視的立場より行われている。しかし、この巨視的立場に立ったとしても土や岩盤を連続体と見なすには一般的にあまりにも不均一であり、また、不均質でもあるため粒状体として、すなわち、
不連続体として取り扱うべきであろう。さらに、土や岩盤の節理などは引っ張りに弱く、亀裂が入りやすいとか外力の作用によって相対的にずれやすい性質もある。
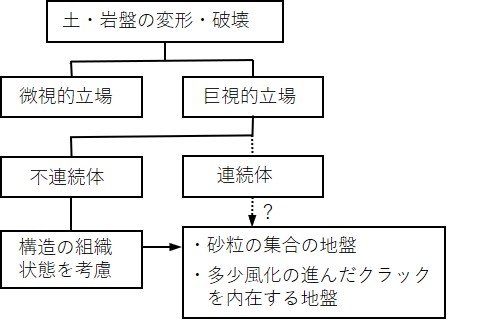
$\hspace{6em}$図1.1 地盤の破壊
したがって、土や岩盤などの解析では上述の概念を取り入れた、すなわち、不連続体としての取扱いが是非必要となる。このような観点から土質力学においては
極限解析法や
極限平衡法が古くより導入され、
簡易解析法として広く使われてきたのは当然の帰結であった。現在でも実設計の面で幅広く利用されている。しかし、このような方法には限界がある。この理由は、これらの方法に荷重増分法的取扱いが全く取り入れられていないこと、応力の平衡は考えるが変位についてはあまり考えない粗っぽい解析法であること、また、土の力学的性質に多くの不明な点が残るため、土を
剛塑性体に近似して境界の速度条件に適合する塑性流れ場の速度系（可容速度）を見つけだすことが精一杯であったことによる。実際の複雑な地盤においては、このような可容速度場を見つけることは極めて困難であり、古典的解析法の利用範囲が制限されるのも頷ける。
先に説明した有限要素法でも、上述のような不連続性の概念を取り入れる方法が幾つか提案されている。Goodmanは有限要素法解析において不連続性を取り入れるため、定ひずみ要素の間に「
ジョイント要素」と呼ばれる
不連続要素を導入している。この方法によれば、土や岩盤に内存する亀裂や断層などを表現することができる。しかし、すべりや引っ張り破壊などによって生ずる破壊は予め想定することが難しく、このような観点では、得られる解が定ひずみ要素の性質に依存する場合も多い。また、鉄筋コンクリートのクラック解析に用いるため「
結合要素」と呼ばれる不連続要素がNgoらによって提案されている。川本らは要素内を再分割することで不連続性を導入する方法を提案しているが、この方法はクラックが発生する度に自由度の設定を変えなければならない。また、最近ではCundallによる
個別要素法も地盤工学諸問題に適用され、不連続性を表現する有力な手法に成長しつつある。
一方、川井は塑性変形や破壊の本質はすべりにあるとして新しい離散化モデルを1976年に発表した。このモデルでは要素自身を剛体と仮定し、要素分割を行うことによって生ずる各要素境界面上に体積変化およびせん断変形に抵抗する２種類のばねを設け、要素内の仕事の代わりに要素境界面上に集中化された表面力の仕事を用いてエネルギーを評価する。その結果、増分計算を行うことにより、自動的にすべり面を決定することができる。このようなモデルの特徴から、本モデルのことを
剛体－ばねモデル（Rigid Bodies-Spring Model:RBSM）あるいは
川井モデルと呼んでいる。
川井モデルは、先の理由から要素内応力分布は考えていないが、崩壊機構条件と要素間の表面力の釣合条件を満足しているため、崩壊荷重に対する
上界値を与えることがわかる。すなわち、本モデルは一般化された極限解析用のモデルと位置付けることができ、しかも、変位パラメータとして重心に剛体変位を設定するため、要素間の切断を簡単に行うことができる。
当初、本モデルは金属構造物の極限解析に利用され、その実用性はほぼ実証されてきた。金属材料のように結晶から構成される硬い材料と土のような粒状体から形成される比較的ゆるく詰まった物質では自ずからその性質も異なるが、いずれの材料もその塑性変形や破壊がすべりという変位場の不連続性に支配されていることは疑問の余地のない所である。
ただし、土のような粒状体は引っ張りに対する抵抗力が弱く、たとえ抵抗したとしてもその力は、金属材料と比べものにならない程ごく僅かでしかないということに注意しなければならない。多くの地盤ではこのような場合、
引張クラックが発生するが、地盤の安定問題においてこの引張クラックは地盤全体の安全率にも影響を及ぼす重要な要因の一つである。 従来の極限解析手法にこのような引張クラックの概念を導入することは極めて困難であり、引張クラックの長さを予め仮定して解析することがよく行われている。しかし、川井モデルでは先に述べたように、接触型のクラックに対する取扱いが簡単であり、マクロ的な亀裂の導入、成長や再接触などの表現を最も得意とするモデルである。
このように、川井モデルの地盤工学への適用は極限解析手法の新しい局面を生む可能性を秘めている。そこで、本章では、
2章以降に述べる地盤解析への応用に対する準備として、川井モデルの概要を整理しながら説明する。
有限要素法と同様、川井モデルにおいても
図1.2 に示すような各種の要素ライブラリーが用意されている。これらの基本的な考え方については「剛体－ばねモデルと離散化極限解析法概論」（川井忠彦著）に示されているが、本節においても再度これらの要素を具体的に誘導してみよう。ただし、シェル要素については「鋼構造の離散化極限解析」（都井裕著）に詳細が示されているため、ここでは省略する。
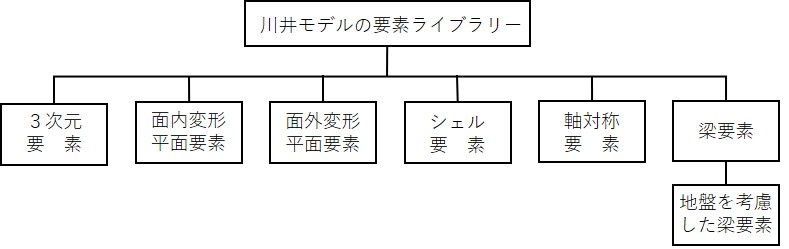
$\hspace{10em}$図1.2 川井モデルの要素ライブラリー
（１）３次元要素
いま、
図1.3 に示すような沢山の３次元剛体要素の集合体を考える。このとき、接触面の形状が既知であれば、互いに接触している剛体要素を取り出し、接触境界面上の任意点における体積変化ならびにせん断変形に対応する相対変位を拘束する２種類のばねを連続的に分布させる。剛性行列はこの接触面上のばねに集中化されたエネルギーを評価することで誘導することができる。
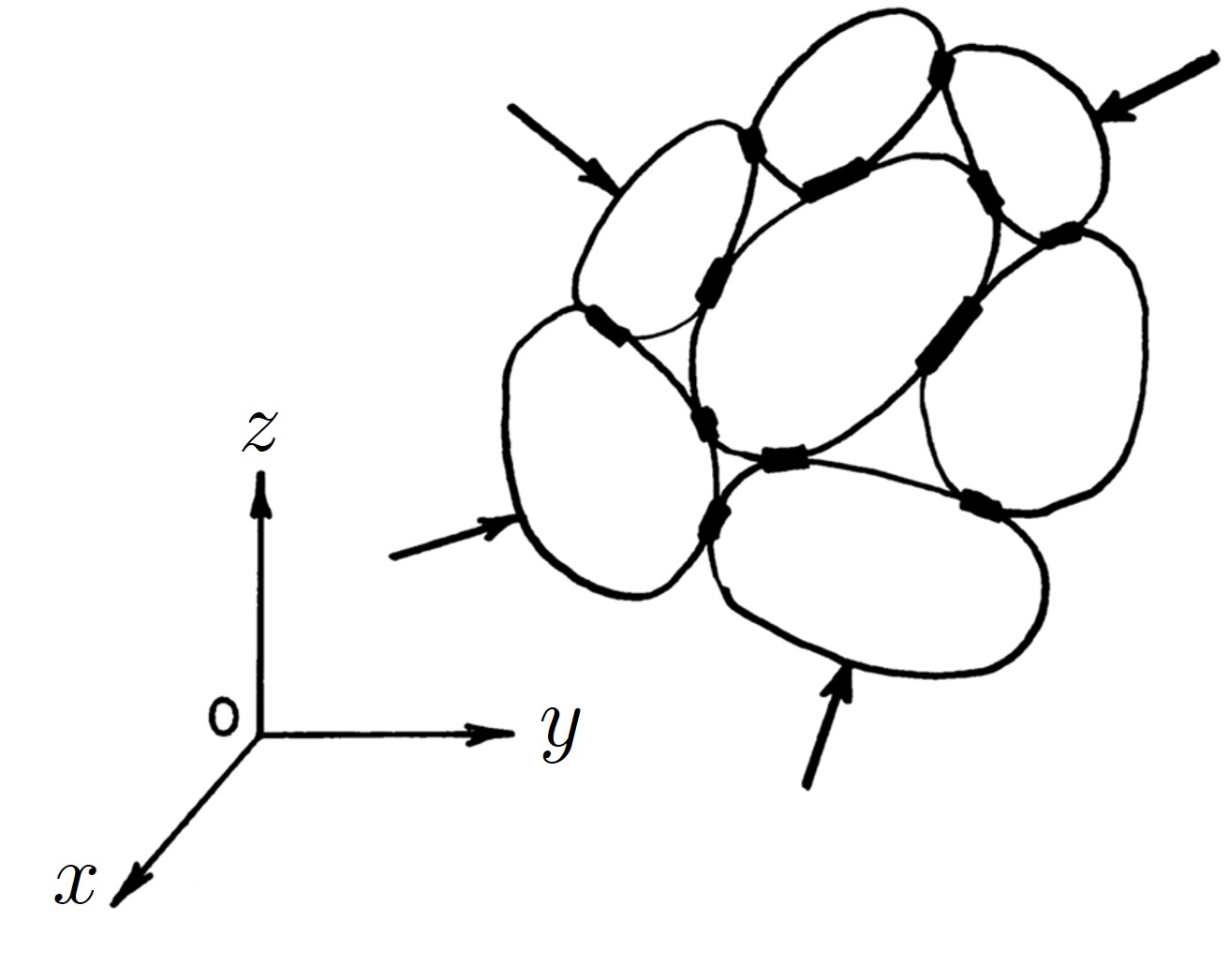
$\hspace{1em}$図1.3 ３次元剛体要素の集合
しかし、実際には任意の形状を持った物体の接触面形状を決定することは容易でなく、特に、川井モデルの特徴が生きてくる強非線形問題の場合、解析的にそれを誘導することはほとんど不可能に近い。
一方、有限要素法のように、与えられた領域を４面体や６面体に分割するならば、隣接する要素の境界面は三角形や四角形となり、微小変形を仮定した場合、容易に接触面の形状を決定することができる。ここでは、このような仮定のもとに
３次元剛体要素の剛性行列を誘導してみよう。
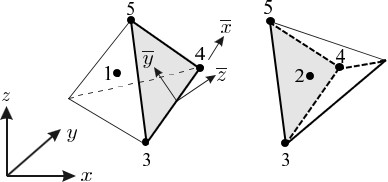
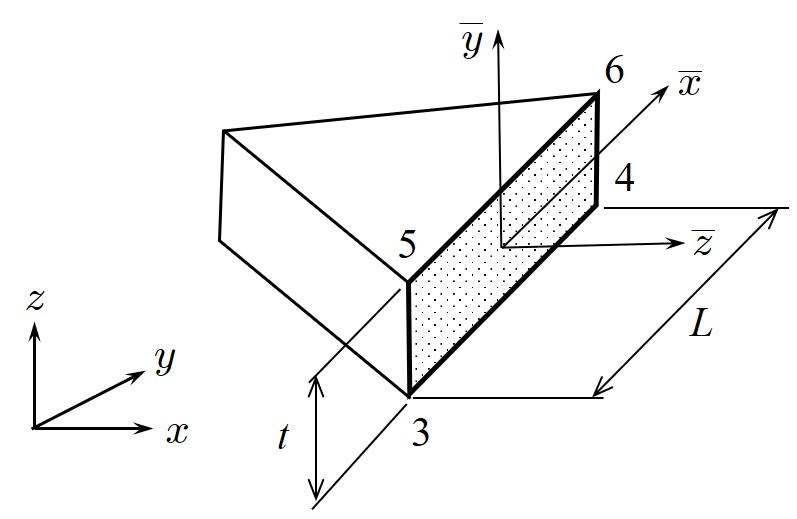
$\hspace{6em}$図1.4 ４面体要素と座標系
図1.4には４面体を仮定した２つの剛体が示されている。図中、網掛けで塗りつぶされた部分が接触面を表している。いま、各剛体の重心における
剛体変位を $\boldsymbol{u}_i$ とし、
図1.5に示す向きを正の方向と考える。
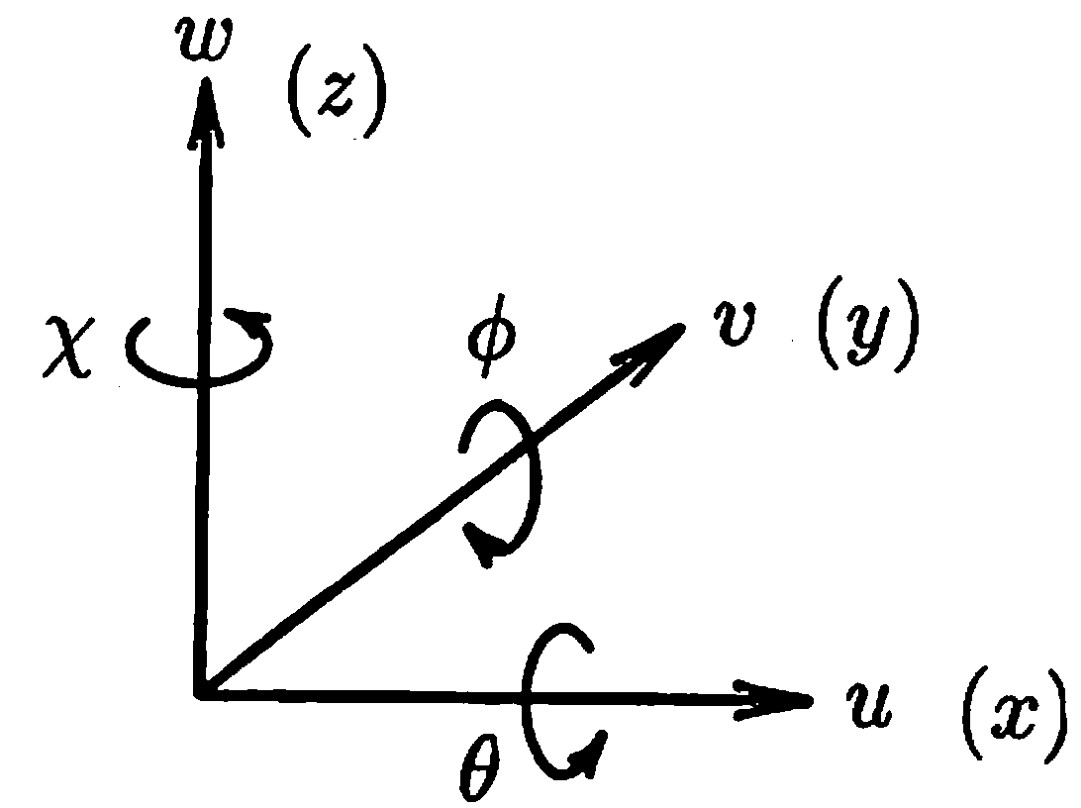
$\hspace{0em}$図1.5 ３次元剛体要素の自由度
このとき、各剛体内の任意点における
変位ベクトル $\boldsymbol{U}_i$ は剛体の運動学より重心の剛体変位 $\boldsymbol{u}_i$ を用いて以下のように表すことができる。
\[{\rm (1.1)}
\boldsymbol{U}_i=\boldsymbol{Q}_i \cdot \boldsymbol{u}_i
\]
ここで、$\boldsymbol{U}_i$、$\boldsymbol{u}_i$、$\boldsymbol{Q}_i$ の成分は以下の通りである。
\[\hspace{2em}
\boldsymbol{U}_1 = ( U_1 \;\; V_1 \;\; W_1 )^t \;, \;\;\;\;
\boldsymbol{U}_2 = ( U_2 \;\; V_2 \;\; W_2 )^t
\]
\[\hspace{2em}
\boldsymbol{u}_1 = ( u_1 \;\; v_1 \;\; w_1 \;\;
\theta_1 \;\; \phi_1 \;\; \chi_1 )^t \;, \;\;\;\;
\boldsymbol{u}_2 = ( u_2 \;\; v_2 \;\; w_2 \;\;
\theta_2 \;\; \phi_2 \;\; \chi_2 )^t
\]
\[\hspace{2em}
\boldsymbol{Q}_1 =
\left[
\begin{array}{cccccc}
1 & 0 & 0 & \;\;\; 0 & \;\;\; (z-z_1) & -(y-y_1) \\
0 & 1 & 0 & -(z-z_1) & \;\;\; 0 & \;\;\; (x-x_1) \\
0 & 0 & 1 & \;\;\; (y-y_1) & -(x-x_1) & \;\;\; 0 \\
\end{array}
\right]
\]
\[\hspace{2em}
\boldsymbol{Q}_2 =
\left[
\begin{array}{cccccc}
1 & 0 & 0 & \;\;\; 0 & \;\;\; (z-z_2) & -(y-y_2) \\
0 & 1 & 0 & -(z-z_2) & \;\;\; 0 & \;\;\; (x-x_2) \\
0 & 0 & 1 & \;\;\; (y-y_2) & -(x-x_2) & \;\;\; 0
\end{array}
\right]
\]
また、下付きの添字は各剛体の要素番号を表すものとし､ $(x_i,y_i,z_i)$ は各要素の重心点における座標値を示しているものとする。
川井モデルでは隣接する２要素間の相対変位を利用するため、剛体内における任意点の変位ベクトル $U_i$ を
図1.4 に示すような三角形の一辺を座標軸とする局所座標系の変位に変換しておくと便利である。
式(1.2)はこの全体座標系と局所座標系の関係を表したものである。
\[{\rm (1.2)}
\overline{\boldsymbol{U}}_i = \boldsymbol{R} \cdot \boldsymbol{U}_i
\]
ここに、上付きの￣は局所座標系に関する物理量を表しており、局所座標系の変位ベクトル $\overline{\boldsymbol{U}}_i$ の成分は以下のようになる。
\[\hspace{2em}
\overline{\boldsymbol{U}}_1 = ( \overline{U}_1 \;\;
\overline{V}_1 \;\;
\overline{W}_1 )^t \;, \;\;\;\;
\overline{\boldsymbol{U}}_2 = ( \overline{U}_2 \;\;
\overline{V}_2 \;\;
\overline{W}_2 )^t
\]
また、$\boldsymbol{R}$ は
座標変換行列で、方向余弦 $(l_i,m_i,n_i)$ を用い以下のように表される。
\[\hspace{2em}
\boldsymbol{R} =
\left[
\begin{array}{ccc}
l_1 & m_1 & n_1 \\
l_2 & m_2 & n_2 \\
l_3 & m_3 & n_3
\end{array}
\right]
\]
各方向余弦は、
図1.4に示されるような三角形の各頂点における座標値を用いて以下のように定義される。
\[\hspace{2em}
l_{1} = \frac{x_{43}}{L} \;, \;\;\;\;
m_{1} = \frac{y_{43}}{L} \;, \;\;\;\;
n_{1} = \frac{z_{43}}{L}
\]
\[\hspace{2em}
l_{2} \;\; =
\left(
\begin{array}{c}
z_{43}
\left|
\begin{array}{cc}
z_{43} & x_{43} \\
z_{53} & x_{53}
\end{array}
\right|
-y_{43}
\left|
\begin{array}{cc}
x_{43} & y_{43} \\
x_{53} & y_{53}
\end{array}
\right|
\end{array}
\right) /(2AL)
\]
\[\hspace{2em}
m_{2} =
\left(
\begin{array}{c}
x_{43}
\left|
\begin{array}{cc}
x_{43} & y_{43} \\
x_{53} & y_{53}
\end{array}
\right|
-z_{43}
\left|
\begin{array}{cc}
y_{43} & z_{43} \\
y_{53} & z_{53}
\end{array}
\right|
\end{array}
\right) /(2AL)
\]
\[\hspace{2em}
n_{2} \; =
\left(
\begin{array}{c}
y_{43}
\left|
\begin{array}{cc}
y_{43} & z_{43} \\
y_{53} & z_{53}
\end{array}
\right|
-x_{43}
\left|
\begin{array}{cc}
z_{43} & x_{43} \\
z_{53} & x_{53}
\end{array}
\right|
\end{array}
\right) /(2AL)
\]
\[\hspace{2em}
l_{3} =
\left|
\begin{array}{cc}
y_{43} & z_{43} \\
y_{53} & z_{53}
\end{array}
\right|
/(2A) \;, \;\;\;\;
m_{3} =
\left|
\begin{array}{cc}
z_{43} & x_{43} \\
z_{53} & x_{53}
\end{array}
\right|
/(2A) \;, \;\;\;\;
n_{3} =
\left|
\begin{array}{cc}
x_{43} & y_{43} \\
x_{53} & y_{53}
\end{array}
\right|
/(2A)
\]
ここで、$L$ は三角形の一辺 $\overline{34}$ の長さを、また、$A$ は三角形の面積を表しており、三角形の頂点座標により以下のように求められる。
\[\hspace{2em}
L = \sqrt{x^{2}_{43}+y^{2}_{43}+z^{2}_{43}} \;, \;\;\;\;
2A = \sqrt{
\left|
\begin{array}{cc}
y_{43} & z_{43} \\
y_{53} & z_{53}
\end{array}
\right|^{2}
+
\left|
\begin{array}{cc}
z_{43} & x_{43} \\
z_{53} & x_{53}
\end{array}
\right|^{2}
+
\left|
\begin{array}{cc}
x_{43} & y_{43} \\
x_{53} & y_{53}
\end{array}
\right|^{2}
}
\]
この結果、隣接する２つの剛体の接触面における
相対変位 $\delta$ は以下のように簡単に表すことができる。
\[{\rm (1.3)}
\boldsymbol{\delta} = \sum_{i=1}^2
\boldsymbol{M}_i \cdot \overline{\boldsymbol{U}}_i
\]
それぞれの、成分は以下に示す通りである。
\[\hspace{2em}
\boldsymbol{\delta} = ( \delta_{s \overline{x}} \;\;
\delta_{s \overline{y}} \;\;
\delta_{n} )^{t} \;, \;\;\;\;
{\bf M}_{1} =
\left[
\begin{array}{rrr}
-1 & 0 & 0 \\
0 & -1 & 0 \\
0 & 0 & -1
\end{array}
\right] \;, \;\;\;\;
\boldsymbol{M}_{2} =
\left[
\begin{array}{ccc}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1
\end{array}
\right]
\]
以上の結果を整理すると、最終的に要素重心の剛体変位により２要素間の相対変位が以下のように求められる。
\[{\rm (1.4)}
\boldsymbol{\delta} = \sum_{i=1}^{2}
\boldsymbol{M}_i \cdot
\boldsymbol{R} \cdot
\boldsymbol{Q}_i \cdot
\boldsymbol{u}_i
= \sum_{i=1}^{2}\boldsymbol{B}_i \boldsymbol{u}_i \;\;\;\;
( \boldsymbol{B}_i = \boldsymbol{M}_i \cdot
\boldsymbol{R} \cdot
\boldsymbol{Q}_i)
\]
ここで、$\boldsymbol{B}$ は有限要素法における節点変位とひずみを関係付けるマトリックスと同様な役割を担っており、川井モデルの場合、要素重心の剛体変位と要素間の相対変位を関係付けている。$\boldsymbol{B}$ の成分を示すと以下のようである。
\[
\boldsymbol{B}_{1} =
\left[
\begin{array}{llllll}
-l_{1}&-m_{1}&-n_{1}&
m_{1}(\!z\!-\!z_{1}\!)\!-\!n_{1}(\!y\!-\!y_{1}\!) &
n_{1}(\!x\!-\!x_{1}\!)\!-\!l_{1}(\!z\!-\!z_{1}\!) &
l_{1}(\!y\!-\!y_{1}\!)\!-\!m_{1}(\!x\!-\!x_{1}\!) \\
-l_{2}&-m_{2}&-n_{2}&
m_{2}(\!z\!-\!z_{1}\!)\!-\!n_{2}(\!y\!-\!y_{1}\!) &
n_{2}(\!x\!-\!x_{1}\!)\!-\!l_{2}(\!z\!-\!z_{1}\!) &
l_{2}(\!y\!-\!y_{1}\!)\!-\!m_{2}(\!x\!-\!x_{1}\!) \\
-l_{3}&-m_{3}&-n_{3} &
m_{3}(\!z\!-\!z_{1}\!)\!-\!n_{3}(\!y\!-\!y_{1}\!) &
n_{3}(\!x\!-\!x_{1}\!)\!-\!l_{3}(\!z\!-\!z_{1}\!) &
l_{3}(\!y\!-\!y_{1}\!)\!-\!m_{3}(\!x\!-\!x_{1}\!)
\end{array}
\right]
\]
\[
\boldsymbol{B}_{2} =
\left[
\begin{array}{lllrrr}
l_{1}&m_{1}&n_{1}&
-m_{1}(\!z\!-\!z_{2}\!)\!+\!n_{1}(\!y\!-\!y_{2}\!) &
-n_{1}(\!x\!-\!x_{2}\!)\!+\!l_{1}(\!z\!-\!z_{2}\!) &
-l_{1}(\!y\!-\!y_{2}\!)\!+\!m_{1}(\!x\!-\!x_{2}\!) \\
l_{2}&m_{2}&n_{2}&
-m_{2}(\!z\!-\!z_{2}\!)\!+\!n_{2}(\!y\!-\!y_{2}\!) &
-n_{2}(\!x\!-\!x_{2}\!)\!+\!l_{2}(\!z\!-\!z_{2}\!) &
-l_{2}(\!y\!-\!y_{2}\!)\!+\!m_{2}(\!x\!-\!x_{2}\!) \\
l_{3}&m_{3}&n_{3} &
-m_{3}(\!z\!-\!z_{2}\!)\!+\!n_{3}(\!y\!-\!y_{2}\!) &
-n_{3}(\!x\!-\!x_{2}\!)\!+\!l_{3}(\!z\!-\!z_{2}\!) &
-l_{3}(\!y\!-\!y_{2}\!)\!+\!m_{3}(\!x\!-\!x_{2}\!)
\end{array}
\right]
\]
さて、ばね構造では荷重と変形の間に $P = k \cdot \delta$ なる関係が成立するが、川井モデルにおいても同様な考えにより、要素境界面上の相対変位と表面力の間に以下のような関係があるものと仮定する。
\[{\rm (1.5)}
\boldsymbol{\sigma} = \boldsymbol{D} \cdot \boldsymbol{\delta}
\]
ここで、$\boldsymbol{D}$ はばね構造で言うところの $k$、すなわち、
ばね係数行列である。１次元ばね構造の場合、ばねの種類は１つだけであったが、本モデルのように３次元の運動を拘束するためには各方向の変形に抵抗するばねを設けなければならない。ここでは、接触面に設けた局所座標系における法線方向、すなわち、$\overline{z}$ 方向の体積変化に抵抗するばねを $k_n$、また、$\overline{x}$ 方向、$\overline{y}$ 方向のせん断変形に抵抗するばねを、それぞれ $k_{s \overline{x}}$、$k_{s\overline{y}}$ として以下のように $\boldsymbol{D}$ 行列を表す。
\[\hspace{2em}
\boldsymbol{D} =
\left[
\begin{array}{ccc}
k_{s \overline{x}} & 0 & 0 \\
0 & k_{s \overline{y}} & 0 \\
0 & 0 & k_{n}
\end{array}
\right]
\]
また、$\boldsymbol{\sigma}$ は要素境界面上における単位面積当たりの
表面力であり、局所座標系の各方向に沿って以下のような３つの成分を持つ。
\[\hspace{2em}
\boldsymbol{\sigma} = ( \tau_{s \overline{x}} \;\;
\tau_{s \overline{y}} \;\;
\sigma_{n} )^{t}
\]
前者の２つがせん断応力、３番目が垂直応力に対応している。
次に、４面体の重心から接触面に下した垂線の高さを基準として差分化された一軸状態のひずみを、相対変位により以下のように仮定する。
\[{\rm (1.6)}
\boldsymbol{\varepsilon} = \frac{1}{h} \boldsymbol{\delta}
\;\;\;\; (h=h_{1}+h_{2})
\]
ただし、$\boldsymbol{\varepsilon}$ 成分は以下の通りである。
\[\hspace{2em}
\boldsymbol{\varepsilon} = ( \gamma_{s \overline{x}} \;,\;
\gamma_{s \overline{y}} \;,\;
\varepsilon_{n} )^{t}
\]
一方、一軸状態の応力－ひずみ関係は
\[{\rm (1.7)}
\sigma_{n} =
\frac{(1-\nu)E}{(1+\nu)(1-2\nu)} \cdot \varepsilon_{n} \;, \;\;\;
\tau_{s \overline{x}} =
\frac{E}{(1+\nu)} \cdot \gamma_{s \overline{x}} \;, \;\;\;
\tau_{s \overline{y}} =
\frac{E}{(1+\nu)} \cdot \gamma_{s \overline{y}}
\]
と表せることから、先の
ばね定数が以下のように決定される。
\[{\rm (1.8)}
k_{n} = \frac{(1-\nu)E}{(1+\nu)(1-2\nu)h} \;, \;\;\;
k_{s \overline{x}} = \frac{E}{(1+\nu)h} \;, \;\;\;
k_{s \overline{y}} = \frac{E}{(1+\nu)h}
\]
なお、このようなばね定数の決定方法は便宜上のものであり、一般的には実験値や計測値から推定することも可能である。特に、断層などのジョイントを表現するためには後者の実験、実測などから決定した方がよいであろう。
このようにして、変形後に２要素間の分布ばね系に蓄えられるエネルギーが以下のように求められる。
\[{\rm (1.9)}
V = \frac{1}{2} \int_{A}(\boldsymbol{\delta}^{t} \cdot
\boldsymbol{D} \cdot
\boldsymbol{\delta}) d\!A
= \frac{1}{2} \boldsymbol{u}^{t}
\int_{A} \boldsymbol{B}^{t} \boldsymbol{D} \boldsymbol{B} d\!A \; \boldsymbol{u}
\]
ここで、$\boldsymbol{B}=[\boldsymbol{B}_1 \;\boldsymbol{B}_2]$ である。したがって、Castigliano の定理から一つの接触面に対する
剛性方程式が以下のように得られる。
\[{\rm (1.10)}
\boldsymbol{F} = \frac{\partial V}{\partial \boldsymbol{\delta}}
= \boldsymbol{K} \cdot \boldsymbol{u}
\]
ここで、$\boldsymbol{F}$ は外力であり、その成分は $X_i$、$Y_i$、$Z_i$ を各座標軸方向の力とし、$L_i$、$M_i$、$N_i$ をモーメントとして以下のように表せる。
\[\hspace{2em}
\boldsymbol{F} = (X_{1},Y_{1},Z_{1},L_{1},M_{1},N_{1} ;
X_{2},Y_{2},Z_{2},L_{2},M_{2},N_{2})
\]
また、$\boldsymbol{u}$ は重心の剛体変位で、その成分は以下に示される。
\[\hspace{2em}
\boldsymbol{u} = (u_{1},v_{1},w_{1},\theta_{1},\phi_{1},\chi_{1} ;
u_{2},v_{2},w_{2},\theta_{2},\phi_{2},\chi_{2})
\]
ただし、下付きの数字は要素番号を示すものとする。$\boldsymbol{K}$ は
ばね剛性行列で、有限要素法で言うところの要素剛性行列である。
\[\hspace{2em}
\boldsymbol{K} = \int_{A} \boldsymbol{B}^{t} \boldsymbol{D} \boldsymbol{B} d\!A
\]
このばね剛性行列は（１２×１２）となり、有限要素法のそれと同サイズとなっている。この剛性行列の成分には、被積分項が座標の関数となる積分が含まれているが、接触面の形状が既知の場合、簡単に積分を実行することが可能である。この結果については
9章に示しておくのでそれを参考にしてほしい。全体剛性行列はここで求めたばね剛性行列をもとに、要素重心の剛体変位を自由度として有限要素法と同様な手順により重ね合わせを行うことで誘導することができる。この点に関しては「離散化極限解析プログラミング」（竹内則雄著）に詳細が示されている。
（２）面内変形平面要素
面内変形平面要素に限定した要素の誘導ならびにブログラミング技法については「離散化極限解析プログラミング」に詳細が述べられている。そこで、ここでは３次元要素を簡略化することによって面内変形平面要素の剛性行列を誘導してみよう。
まず初めに
図1.4に示した一般的な４面体要素を変形し、
図1.6に示すような三角形平板を考えてみよう。ただし、ここでは便宜上、三角形平板を考えただけであり、実際には平板であれば任意の多角形ないしは円、楕円などが許される。
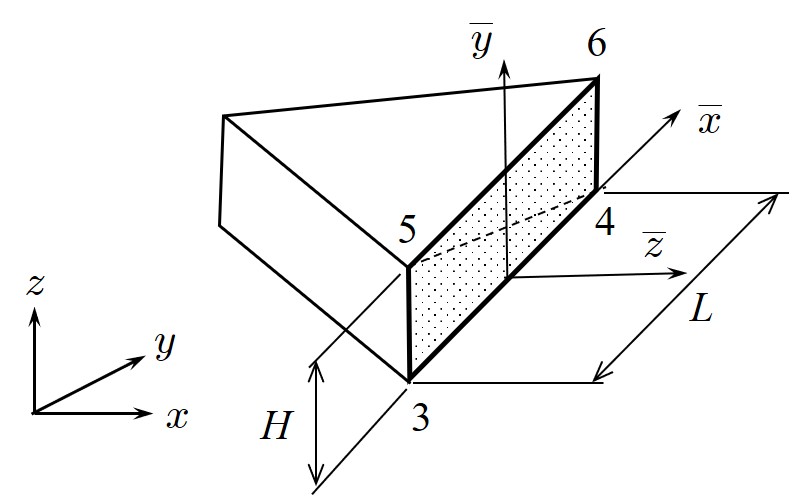
$\hspace{4em}$図1.6 面内変形平面要素
いま、この三角形平板は $x-y$ 平面に平行に置かれているものとする。図中、点で塗りつぶされた長方形が隣接する要素との接触面であり、この面に図に示されるような $\overline{x}$ 軸と $\overline{34}$ 節点が平行で、面の法線方向と $\overline{z}$ 軸が一致する局所座標系を設ける。全体座標系と局所座標系との間には、$x-y$ 平面と $\overline{z}-\overline{x}$ 平面が平行で、しかも $z$ 軸と $\overline{y}$ 軸が平行であるという関係が成立しているものとする。このように考えると、３次元の方向余弦は以下のようになる。
\[\hspace{2em}
l_{1} = \frac{x_{43}}{L} \;, \;\;\;\;
m_{1} = \frac{y_{43}}{L}
\]
\[\hspace{2em}
l_{3} =
\left|
\begin{array}{cc}
y_{43} & z_{43} \\
y_{53} & z_{53}
\end{array}
\right|
/(2A) = \frac{y_{43}}{L}\;, \;\;\;\;
m_{3} =
\left|
\begin{array}{cc}
z_{43} & x_{43} \\
z_{53} & x_{53}
\end{array}
\right|
/(2A) = - \frac{x_{43}}{L}
\]
\[\hspace{2em}
L = \sqrt{x^{2}_{43}+y^{2}_{43}} \;, \;\;\;\;
( 2A = H \times L = z_{53} \times L )
\]
この結果、方向余弦は辺 $\overline{34}$ の長さと節点3、4の $(x,y)$ 座標だけが利用され、接触面の面積は無関係となることが理解できよう。
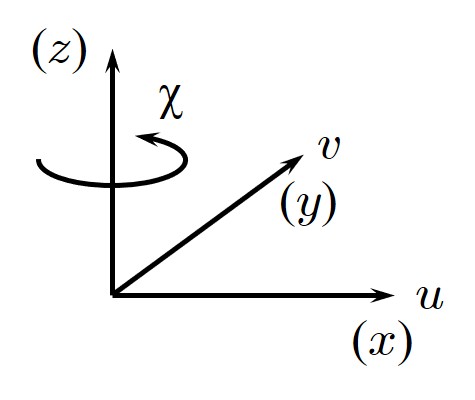
$\hspace{0em}$図1.7 面内変形平面要素の自由度
また、面内変形平面問題の場合、自由度は
図1.7に示されるように $x-y$ 平面における平行変位 $(u,v)$ と $z$ 軸回りの回転 $(\chi)$ の３自由度になるため、３次元に関する剛体内の 任意点における変位ベクトル $\boldsymbol{U}_i$ を表わす
式(1.1)は以下のように簡略化される。
\[{\rm (1.11)}
\boldsymbol{U}_i = \boldsymbol{Q}_i \cdot \boldsymbol{u}_i
\]
ここに、$\boldsymbol{U}_i$、$\boldsymbol{u}_i$、$\boldsymbol{Q}_i$ は以下の通りである。
\[\hspace{2em}
\boldsymbol{U}_{1} = ( U_{1} \;\; V_{1} )^{t} \;, \;\;\;\;
\boldsymbol{U}_{2} = ( U_{2} \;\; V_{2} )^{t} \;, \;\;\;\;
\boldsymbol{u}_{1} = ( u_{1} \;\; v_{1} \;\; \chi_{1} )^{t} \;, \;\;\;\;
\boldsymbol{u}_{2} = ( u_{2} \;\; v_{2} \;\; \chi_{2} )^{t}
\]
\[\hspace{2em}
\boldsymbol{Q}_{1} =
\left[
\begin{array}{ccc}
1 & 0 & -(y-y_{1}) \\
0 & 1 & \;\;\; (x-x_{1})
\end{array}
\right] \;, \;\;\;\;
\boldsymbol{Q}_{2} =
\left[
\begin{array}{ccc}
1 & 0 & -(y-y_{2}) \\
0 & 1 & \;\;\; (x-x_{2}) \\
\end{array}
\right]
\]
このように、面内変形平面要素では $z$ 軸方向の変位が生じないため、変位ベクトルも $x$ 軸、$y$ 軸方向に関する２成分のみとなり、また、$\boldsymbol{Q}_i$ も $x$ と $y$ だけの行列となる。
全体座標系の変位ベクトルは
図1.6に示される座標系を用い、以下のように局所座標系の変位ベクトルと関係付けることができる。
\[{\rm (1.12)}
\overline{\boldsymbol{U}}_i = \boldsymbol{R} \cdot \boldsymbol{U}_i
\]
ここで、局所座標系の変位ベクトル $\overline{\boldsymbol{U}}_i$ ならびに座標変換行列 $\boldsymbol{R}$ は以下のようになる。
\[\hspace{2em}
\boldsymbol{\overline{U}}_{1} = ( \overline{U}_{1} \;\;
\overline{W}_{1} )^{t} \;, \;\;\;\;
\boldsymbol{\overline{U}}_{2} = ( \overline{U}_{2} \;\;
\overline{W}_{2} )^{t} \;, \;\;\;\;
\boldsymbol{R} =
\left[
\begin{array}{cc}
l_{1} & m_{1} \\
l_{3} & m_{3}
\end{array}
\right]
\]
全体座標系における変位ベクトルの成分が $(U_i,V_i)$ であるのに対し、局所座標系における変位ベクトルの成分が $(\overline{U}_i, \overline{W}_i)$ となること、また、方向余弦も $(l_3,m_3)$ が用いられていることに注意してほしい。
この結果、２要素間の相対変位が以下のように求められる。
\[{\rm (1.13)}
\boldsymbol{\delta} = \sum_{i=1}^{2}
\boldsymbol{M}_i \cdot \overline{\boldsymbol{U}}_i
\]
ただし、相対変位は局所座標系の $\overline{z}$ 軸に沿った体積変化に対する $\delta_n$ と $\overline{x}$ 軸に沿ったせん断変形に対する $\delta_s$ の２種類となり、各行列は以下のように簡略化される。
\[\hspace{2em}
\boldsymbol{\delta} = ( \delta_{s} \;\;
\delta_{n} )^{t} \;\;, \;\;\;\;
\boldsymbol{M}_{1} =
\left[
\begin{array}{rrr}
-1 & 0 \\
0 & -1
\end{array}
\right] \;\;, \;\;\;\;
\boldsymbol{M}_{2} =
\left[
\begin{array}{ccc}
1 & 0 \\
0 & 1
\end{array}
\right]
\]
したがって、
式(1.11)、
式(1.12)、
式(1.13)より相対変位は要素重心の剛体変位を用いて以下のように表される。
\[{\rm (1.14)}
\boldsymbol{\delta} = \sum_{i=1}^{2}
\boldsymbol{M}_{i} \cdot
\boldsymbol{R} \cdot
\boldsymbol{Q}_{i} \cdot
\boldsymbol{u}_{i}
= \sum_{i=1}^{2}\boldsymbol{B}_{i}\boldsymbol{u}_{i} \;\;\;\;
(\boldsymbol{B}_{i} = \boldsymbol{M}_i \cdot
\boldsymbol{R} \cdot
\boldsymbol{Q}_i)
\]
ここで、$\boldsymbol{B}$ マトリックスは以下の通りである。
\[\hspace{2em}
\boldsymbol{B}_{1} =
\left[
\begin{array}{lll}
-l_{1}&-m_{1}&l_{1}(\!y\!-\!y_{1}\!)\!-\!m_{1}(\!x\!-\!x_{1}\!) \\
-l_{3}&-m_{3}&l_{3}(\!y\!-\!y_{1}\!)\!-\!m_{3}(\!x\!-\!x_{1}\!)
\end{array}
\right] \;, \;\;\;\;
\boldsymbol{B}_{2} =
\left[
\begin{array}{lll}
l_{1}&m_{1}&-l_{1}(\!y\!-\!y_{2}\!)\!+\!m_{1}(\!x\!-\!x_{2}\!) \\
l_{3}&m_{3}&-l_{3}(\!y\!-\!y_{2}\!)\!+\!m_{3}(\!x\!-\!x_{2}\!)
\end{array}
\right]
\]
面内変形平面要素の場合、局所座標系の $\overline{y}$ 方向に表面力が生じないため、相対変位と表面力の関係は以下のようになる。
\[{\rm (1.15)}
\boldsymbol{\sigma} = \boldsymbol{D} \cdot \boldsymbol{\delta}
\]
以下に、それぞれの行列の成分を示す。
\[
\boldsymbol{\sigma} = ( \tau_{s \overline{x}} \;\;
\sigma_{n} )^{t} \;\;, \;\;\;\;
\boldsymbol{D} =
\left[
\begin{array}{ccc}
k_{s \overline{x}} & 0 \\
0 & k_{n}
\end{array}
\right]
\]
さて、面内変形平面要素に対するばね定数は３次元の場合と同様にして誘導することができる。
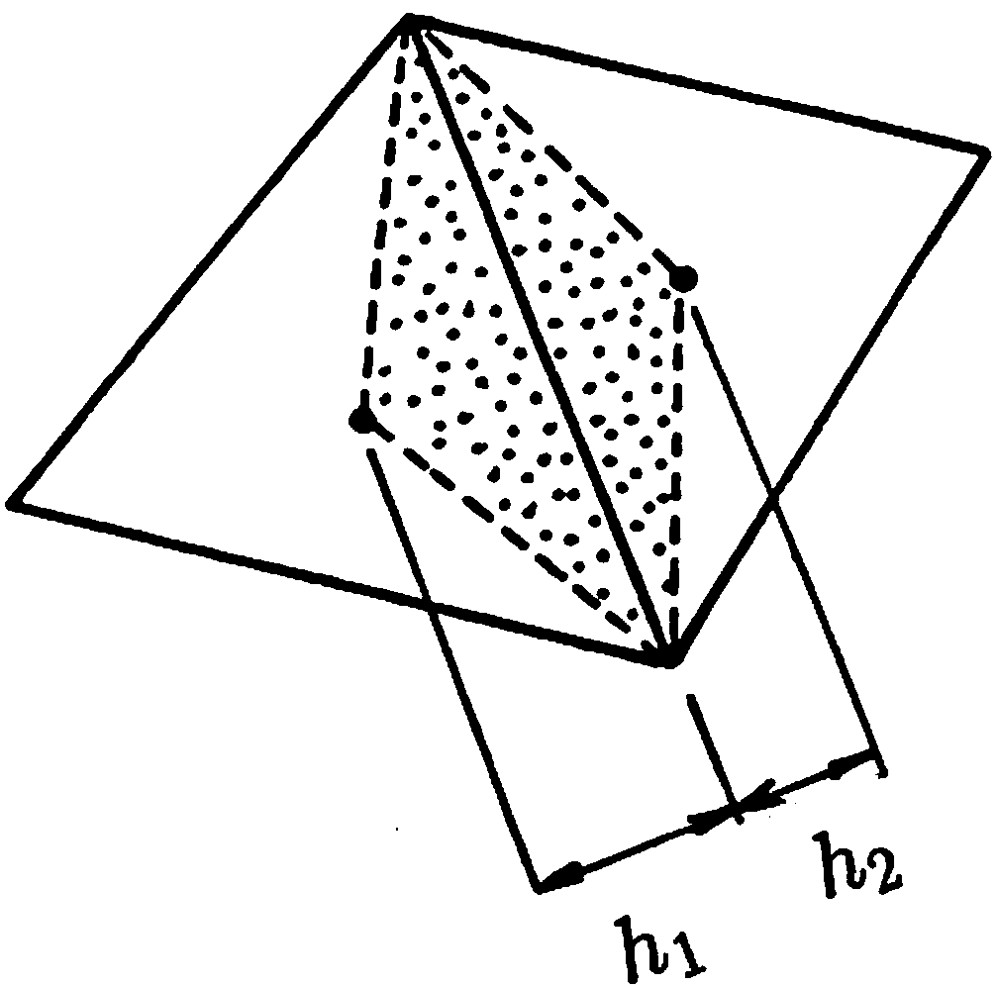
式(1.16)は
図1.8に示される垂線を基準とする単位長さ当たりの相対変位である。
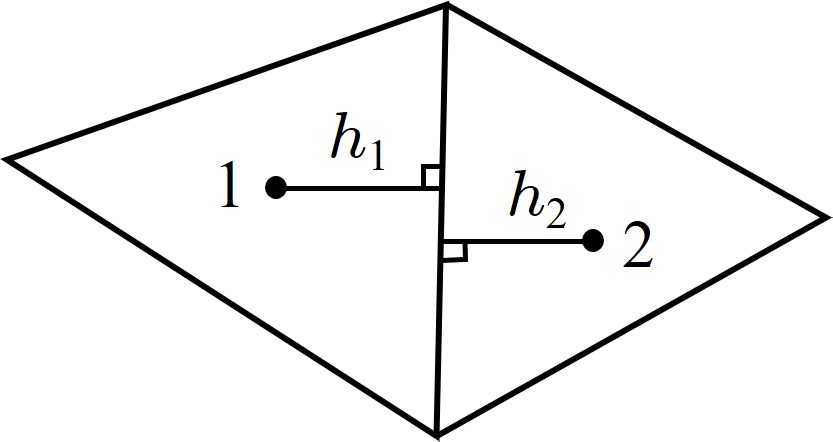
$\hspace{2em}$図1.8 垂線の定義
\[{\rm (1.16)}
\boldsymbol{\varepsilon} = \frac{1}{h} \boldsymbol{\delta} \;\;\;\;
( h = h_{1} + h_{2} )
\]
当然、ひずみも以下に示すよう、局所座標系 $(\overline{x}-\overline{z})$ に沿った２成分となる。
\[\hspace{2em}
\boldsymbol{\varepsilon} = ( \gamma_{s \overline{x}} \;\;
\varepsilon_{n} )^{t}
\]
一方、平面ひずみを仮定した場合、一軸状態の応力とひずみの関係は
\[{\rm (1.17)}
\sigma_{n} =
\frac{(1-\nu)E}{(1+\nu)(1-2\nu)} \cdot \varepsilon_{n} \;, \;\;\;
\tau_{s \overline{x}} =
\frac{E}{(1+\nu)} \cdot \gamma_{s \overline{x}}
\]
であることより、面内変形平面問題のばね定数が以下のように求められる。
\[{\rm (1.18)}
k_{n} = \frac{(1-\nu)E}{(1+\nu)(1-2\nu)h} \;, \;\;\;
k_{s \overline{x}} = \frac{E}{(1+\nu)h}
\]
以上より、３次元の場合と同様に以下の式で与えられるエネルギーを考える。
\[{\rm (1.19)}
V = \frac{1}{2} \int_{S}(\boldsymbol{\delta}^{t} \cdot
\boldsymbol{D} \cdot
\boldsymbol{\delta}) d\!S
\]
ただし、面内変形平面要素では接触面が長方形であるため、積分範囲を３次元とは別な記号 $S$ で表している。２次元要素の場合、板厚を考慮し３次元の場合と同様に面積積分を行う必要があるが、この板厚が一定であるためそれを積分の外に出す事ができ、実際の積分は線積分で済む。
最終的に、面内変形平面要素のばね剛性行列は、
式(1.20)のようにして求めることができる。
\[{\rm (1.20)}
\boldsymbol{F} = \frac{\partial V}{\partial \boldsymbol{\delta}}
= \boldsymbol{K} \cdot \boldsymbol{u}
\]
ただし、$\boldsymbol{F}$ および $\boldsymbol{u}$ は以下に示す通りである。
\[\hspace{2em}
{\bf F} = (X_{1},Y_{1},N_{1} ; X_{2},Y_{2},N_{2}) \;, \;\;\;\;
{\bf u} = (u_{1},v_{1},\chi_{1} ; u_{2},v_{2},\chi_{2})
\]
このように、面内変形平面要素の剛性行列は３次元要素の特殊な場合として簡単に誘導することができ、（６×６）の行列となる。しかし、２次元問題に限定した場合、３次元の場合の記号をそのまま使用することは煩わしいため、２次元独特の表記法を利用することがよく行われている。本書でも、この読み変えと面内変形平面要素の剛性行列を
9章に示してある。
（３）面外変形平面要素
有限要素法では高次の形状関数を用いることによって平板構造解析を行っているが、近藤は低次の形状関数と差分近似を利用して実用的な平板要素を開発している。これをさらに簡略化することにより、都井はせん断変形の影響を無視した川井モデルの平板要素を誘導している。この要素は（４×４）という非常に少ない自由度で解析が可能となっているが、ねじりモーメントの影響は無視されている。著者はせん断変形を無視し、このねじりモーメントを考慮した平板要素を導いている。また、渡辺は保存則表示を利用して平板要素を誘導しているが、この結果は先の３次元に関する川井モデルの特殊な場合として誘導した結果と同じになる。
面外荷重を受ける平板要素はフーチングや連続壁の応力解析などに利用されたりするものの、あまり地盤工学の解析では利用されないが、先の２次元の場合と同様、３次元の特殊な場合として簡単に誘導することができるため、概略のみを説明しておく。
まず初めに
平板要素の座標系を
図1.9に示すよう設定する。設定の方法は基本的に面内変形平面要素の場合と同じであるが、話を簡単にするため、局所座標系の原点を板厚の中心と一致させる。このように考えると平板要素の重心座標のうち $z$ 座標は０となる。すなわち、$z_1=z_2=0$ である。
$\hspace{6em}$図1.9 面外変形平面要素
一方、面外変形平面要素の場合、要素重心の自由度は
図1.10(a)に示すよう、$x$、$y$ 軸における回転と $z$ 方向の平行変位の３種類である。
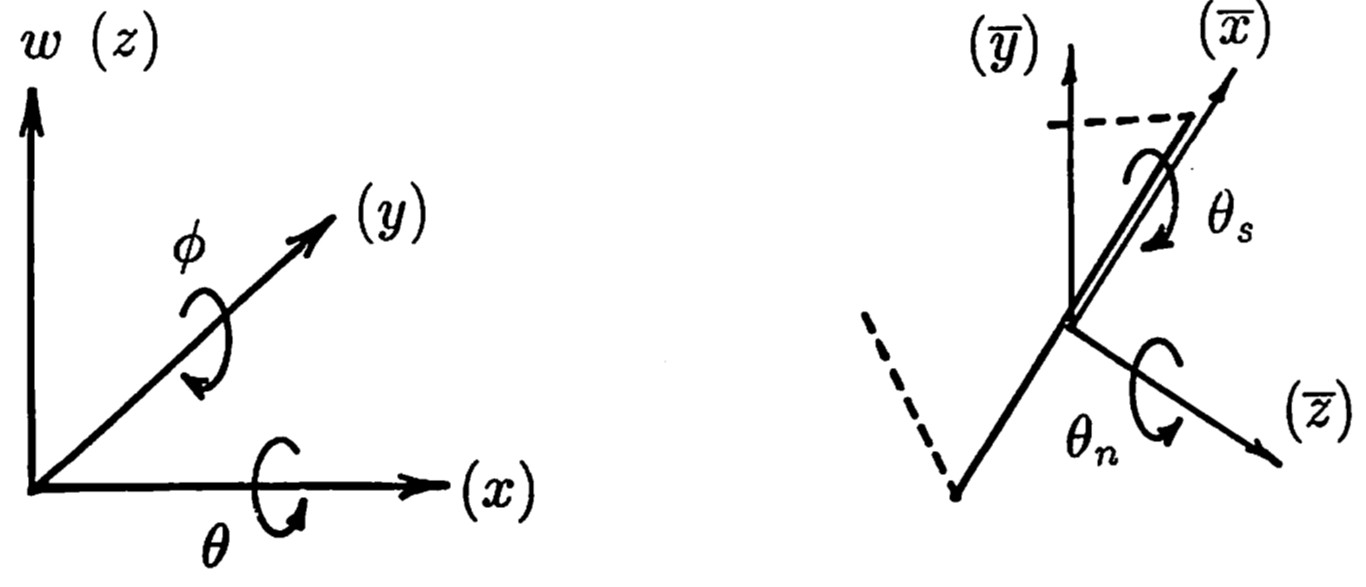$\hspace{3em}$(a) 自由度 $\hspace{6em}$(b) 要素境界面上の変位
$\hspace{3em}$図1.10 要素重心の自由度と境界面上の変位
これらの関係を用いれば、平板内の任意点における変位と要素重心の自由度との間に以下の関係が成立する。
\[{\rm (1.21)}
\boldsymbol{U}_i = \boldsymbol{Q}_i \cdot \boldsymbol{u}_i
\]
ここで、それぞれの行列の成分は以下に示す通りであり、３次元の一般的な
式(1.1)を簡略化した内容となっている。
\[\hspace{2em}
\boldsymbol{U}_{1} = ( U_{1} \;\; V_{1} \;\; W_{1} )^{t} \;, \;\;\;\;
\boldsymbol{U}_{2} = ( U_{2} \;\; V_{2} \;\; W_{2} )^{t}
\]
\[\hspace{2em}
\boldsymbol{u}_{1} = ( w_{1} \;\; \theta_{1} \;\; \phi_{1} )^{t} \;, \;\;\;\;
\boldsymbol{u}_{2} = ( w_{2} \;\; \theta_{2} \;\; \phi_{2} )^{t}
\]
\[\hspace{2em}
\boldsymbol{Q}_{1} =
\left[
\begin{array}{ccc}
0 & \;\;\; 0 & \;\;\; z \\
0 & \; -z & \;\;\; 0 \\
1 & \;\;\; (y-y_{1}) & -(x-x_{1})
\end{array}
\right] \;, \;\;\;\;
\boldsymbol{Q}_{2} =
\left[
\begin{array}{ccc}
0 & \;\;\; 0 & \;\;\; z \\
0 & \; -z & \;\;\; 0 \\
1 & \;\;\; (y-y_{2}) & -(x-x_{2})
\end{array}
\right]
\]
これまでの展開と同様、川井モデルでは要素境界面上の相対変位を利用するため、全体座標系における変位ベクトルを局所座標系の値に変換する。先に示した座標系に従えば、それぞれの方向余弦は
\[\hspace{2em}
l_{1} = \frac{x_{43}}{L} \;, \;\;\;\;
m_{1} = \frac{y_{43}}{L} \;, \;\;\;\;
l_{3} = \frac{y_{43}}{L} \;, \;\;\;\;
m_{3} =-\frac{x_{43}}{L}
\]
\[\hspace{2em}
l_{2} = m_{2} = 0 \;, \;\;\;\;
n_{1} = n_{3} = 0 \;, \;\;\;\;
n_{2} = 1
\]
\[\hspace{2em}
L = \sqrt{x^{2}_{43}+y^{2}_{43}}
\]
となるため、局所座標系と全体座標系の変位ベクトルの間には以下の関係が成立する。
\[{\rm (1.22)}
\boldsymbol{\overline{U}}_{i} = \boldsymbol{R} \cdot \boldsymbol{U}_{i}
\]
ただし、それぞれの行列は以下に示す通りである。
\[\hspace{2em}
\overline{\boldsymbol{U}}_{1} = ( \overline{U}_{1} \;\;
\overline{V}_{1} \;\;
\overline{W}_{1} )^{t} \;, \;\;\;\;
\overline{\boldsymbol{U}}_{2} = ( \overline{U}_{2} \;\;
\overline{V}_{2} \;\;
\overline{W}_{2} )^{t}
\]
\[\hspace{2em}
\boldsymbol{R} =
\left[
\begin{array}{ccc}
l_{1} & m_{1} & 0 \\
0 & 0 & 1 \\
l_{3} & m_{3} & 0
\end{array}
\right]
\]
ここで、これまでの展開に対し物理的な意味を理解するため、
式(1.22)に
式(1.21) の関係を代入し整理してみよう。
\[{\rm (1.23)}
\left.
\begin{array}{l}
\overline{U}_{i} \; = l_{1} \cdot z \cdot \phi_{i}
- m_{1} \cdot z \cdot \theta_{i}
= \overline{\theta}_{s} \cdot z \\[0.5em]
\overline{W}_{i} = l_{3} \cdot z \cdot \phi_{i}
- m_{3} \cdot z \cdot \theta_{i}
= \overline{\theta}_{n} \cdot z \\[0.5em]
\overline{V}_{i} \; = w + (y-y_{i})\theta_{i} - (x-x_{i})\phi_{i}
\end{array}
\right\}
\]
これより、局所座標系における $\overline{x}$ 方向変位 $ \overline{U}_{i}$ は
図1.10(b) に示す要素境界面上における曲げに対する回転角 $(\theta_s)$ に高さ $z$ を掛けたものとなっており、また、$\overline{V}_{i}$ はねじりに対する回転角 $(\theta_n)$ に高さを掛けたものとなっていることが理解できる。
２要素間の相対変位を
式(1.23)の関係を用いて述べるならば相対回転角と相対たわみは、
\[{\rm (1.24)}
\boldsymbol{\delta} = \sum_{i=1}^{2}
\boldsymbol{M}_{i} \cdot \overline{\boldsymbol{U}}_{i}
\]
と表すことができる。ここで、
\[\hspace{2em}
\boldsymbol{\delta} = ( \delta_{s \overline{x}} \;\;
\delta_{s \overline{y}} \;\;
\delta_{n} )^{t}
\]
\[\hspace{2em}
\boldsymbol{M}_{1} =
\left[
\begin{array}{rrr}
-1 & 0 & 0 \\
0 & -1 & 0 \\
0 & 0 & -1
\end{array}
\right] \;, \;\;\;\;
\boldsymbol{M}_{2} =
\left[
\begin{array}{ccc}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1
\end{array}
\right]
\]
である。したがって、これまでの関係を用いれば、この相対変位は各要素重心の剛体変位を用いて次のように表される。
\[{\rm (1.25)}
\boldsymbol{\delta} = \sum_{i=1}^{2}
\boldsymbol{M}_{i} \cdot
\boldsymbol{R} \cdot
\boldsymbol{Q}_{i} \cdot
\boldsymbol{u}_{i}
= \sum_{i=1}^{2}\boldsymbol{B}_{i} \boldsymbol{u}_{i} \;\;\;\;
(\boldsymbol{B}_{i} = \boldsymbol{M}_{i} \cdot
\boldsymbol{R} \cdot
\boldsymbol{Q}_{i})
\]
ここで、$\boldsymbol{B}$ マトリックスの成分は以下に示す通りである。
\[\hspace{2em}
\boldsymbol{B}_{1} =
\left[
\begin{array}{rcc}
0 & m_{1}z & -l_{1}z \\
-1 & -(y-y_{1}) & (x-x_{1}) \\
0 & m_{3}z & -l_{3}z
\end{array}
\right] \;, \;\;\;\;
\boldsymbol{B}_{2} =
\left[
\begin{array}{rcc}
0 & -m_{1}z & l_{1}z \\
1 & (y-y_{2}) & -(x-x_{2}) \\
0 & -m_{3}z & l_{3}z
\end{array}
\right]
\]
一方、相対変位と単位面積当たりの表面力の間には、
\[{\rm (1.26)}
\boldsymbol{\sigma} = \boldsymbol{D} \cdot \boldsymbol{\delta}
\]
なる関係が成立しているものとする。ここで、それぞれの行列は、
\[\hspace{2em}
\boldsymbol{\sigma} = ( \tau_{s \overline{x}} \;\;
\tau_{s \overline{y}} \;\;
\sigma_{n} )^{t} \;\;, \;\;\;\;
\boldsymbol{D} = \left[
\begin{array}{ccc}
k_{s \overline{x}} & 0 & 0 \\
0 & k_{s \overline{y}} & 0 \\
0 & 0 & k_{n}
\end{array}
\right]
\]
であり、またばね定数は平面応力状態を想定し、以下のように仮定する。
\[{\rm (1.27)}
k_{n} = \frac{E}{(1-\nu^{2})h} \;, \;\;\;
k_{s \overline{x}} = \frac{E}{(1+\nu)h} \;, \;\;\;
k_{s \overline{y}} = \frac{E}{(1+\nu)h}
\]
以上の結果から、
式(1.9)、
式(1.10)と同様の展開を行えば、最終的に面外変形平面要素の剛性行列を得ることができる。この剛性行列の詳細については、
9章にまとめてある。
（４）軸対称要素
有限要素法における軸対称問題の解析ではその対称性より、物体の対称軸を含む平面内の２つの変位成分だけで完全にひずみ状態、あるいは応力状態を定義することができる。川井モデルをこの軸対称問題に適用する場合には、重心に設定されている３つの剛体変位を用いればよい。ここでは、簡単に川井モデルにおける
軸対称要素の定式化について説明する。
軸対称問題と面内変形平面問題との相違点は平面に垂直な方向の応力成分、あるいはひずみ成分の存在である。軸対称状態では半径方向の変位が発生すると自動的に円周方向にひずみが生ずるため、応力も存在する。したがって、円周方向のひずみ成分とそれに付随する応力成分を考慮しなければならない。いま、
図1.11 に示すよう $x$ 座標を半径方向とし、$y$ 軸回りの軸対称要素を考えてみよう。
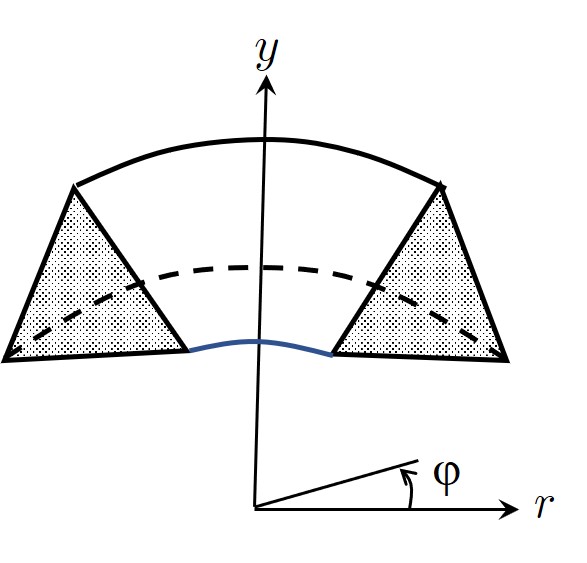$\hspace{1em}$図1.11 軸対称要素
点で塗りつぶされた三角形の重心における剛体変位を自由度と考えれば、三角形面上の任意点の変位ベクトルは、
\[{\rm (1.28)}
\boldsymbol{U}_{i} = \boldsymbol{Q}_{i} \cdot \boldsymbol{u}_{i}
\]
と表される。ただし、$\boldsymbol{U}_i$、$\boldsymbol{u}_i$、$\boldsymbol{Q}_i$ は座標系が異なっていることを除けば、面内変形平面要素の場合と全く同じであり、以下のように表せる。
\[\hspace{2em}
\boldsymbol{U}_{1} = ( U_{1} \;\; V_{1} )^{t} \;, \;\;\;\;
\boldsymbol{U}_{2} = ( U_{2} \;\; V_{2} )^{t}
\]
\[\hspace{2em}
\boldsymbol{u}_{1} = ( u_{1} \;\; v_{1} \;\; \chi_{1} )^{t} \;, \;\;\;\;
\boldsymbol{u}_{2} = ( u_{2} \;\; v_{2} \;\; \chi_{2} )^{t}
\]
\[\hspace{2em}
\boldsymbol{Q}_{1} =
\left[
\begin{array}{ccc}
1 & 0 & -(y-y_{1}) \\
0 & 1 & \;\;\; (r-r_{1})
\end{array}
\right] \;, \;\;\;\;
\boldsymbol{Q}_{2} =
\left[
\begin{array}{ccc}
1 & 0 & -(y-y_{2}) \\
0 & 1 & \;\;\; (r-r_{2}) \\
\end{array}
\right]
\]
この変位ベクトルを
図1.12 に示す記号を用い、一旦、局所座標系の値に変換する。
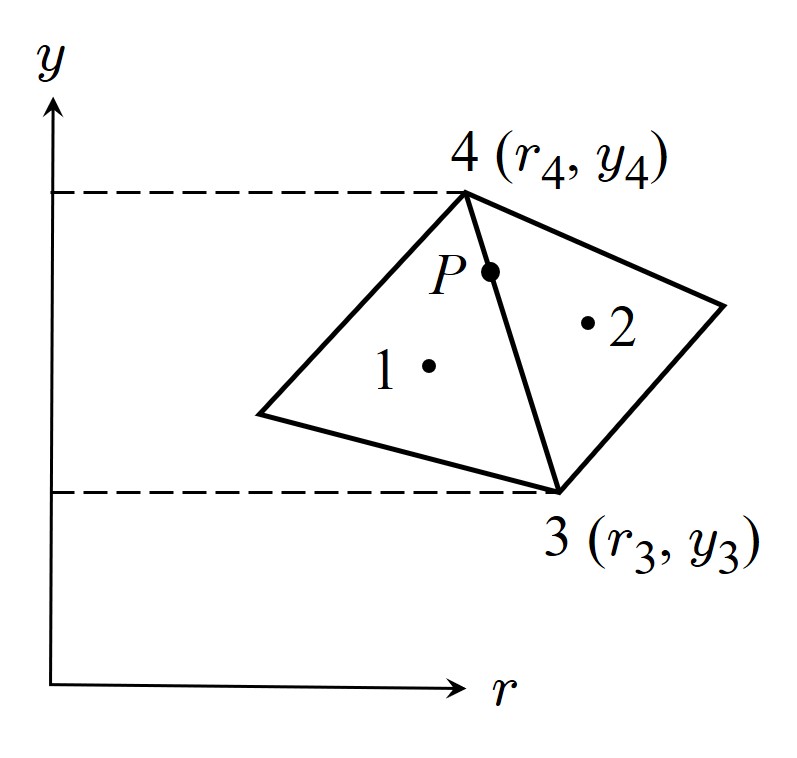$\hspace{2em}$図1.12 軸対称要素の座標系
\[{\rm (1.29)}
\overline{\boldsymbol{U}}_{i} = \boldsymbol{R} \cdot \boldsymbol{U}_{i}
\]
ここで、それぞれの行列は以下に示すように面内変形平面要素の場合と全く同じである。
\[\hspace{2em}
\overline{\boldsymbol{U}}_{1} = ( \overline{U}_{1} \;\;
\overline{W}_{1} )^{t} \;, \;\;\;\;
\overline{\boldsymbol{U}}_{2} = ( \overline{U}_{2} \;\;
\overline{W}_{2} )^{t}
\]
\[\hspace{2em}
\boldsymbol{R} =
\left[
\begin{array}{cc}
l_{1} & m_{1} \\
l_{3} & m_{3}
\end{array}
\right]
\]
\[\hspace{2em}
l_{1} = \frac{r_{43}}{L} \;, \;\;\;\;
m_{1} = \frac{y_{43}}{L} \;, \;\;\;\;
l_{3} = \frac{y_{43}}{L} \;, \;\;\;\;
m_{3} =-\frac{r_{43}}{L}
\]
\[\hspace{2em}
L = \sqrt{r^{2}_{43}+y^{2}_{43}}
\]
次に相対変位について考えてみよう。軸対称問題の場合、半径方向の変位により円周方向のひずみや応力が発生するため、面内の相対変位以外に半径方向の平均変位を求めておく必要がある。そこで、相対変位と半径方向の平均変位を以下のように表す。
\[{\rm (1.30)}
\boldsymbol{\delta} = \sum_{i=1}^{2}
\boldsymbol{M}_{i} \cdot \overline{\boldsymbol{U}}_{i}
\]
ここで、それぞれの行列は
\[\hspace{2em}
\boldsymbol{\delta} = ( \delta_{s} \;\;
\delta_{n} \;\;
\delta_{u} )^{t} \;, \;\;\;\;
\boldsymbol{M}_{1} =
\left[
\begin{array}{ccc}
-1 & \;\; 0 \\
\;\; 0 & -1 \\
l_{1}/2 & l_{3}/2
\end{array}
\right] \;, \;\;\;\;
\boldsymbol{M}_{2} =
\left[
\begin{array}{ccc}
1 & 0 \\
0 & 1 \\
l_{1}/2 & l_{3}/2
\end{array}
\right]
\]
であり、$\delta_u$ が半径方向の平均変位を表している。$l_1$、$l_3$ は座標変換の箇所で説明した方向余弦で、局所座標系の変位ベクトルにこの方向余弦を掛けることで、半径方向の値に戻してある。
このようにして、相対変位と半径方向の平均変位を重心の剛体変位により表すと以下のようになる。
\[{\rm (1.31)}
\boldsymbol{\delta} = \sum_{i=1}^{2}
\boldsymbol{M}_{i} \cdot
\boldsymbol{R} \cdot
\boldsymbol{Q}_{i} \cdot
\boldsymbol{u}_{i}
= \sum_{i=1}^{2}
\boldsymbol{B}_{i} \boldsymbol{u}_{i} \;\;\;\;
(\boldsymbol{B}_{i} = \boldsymbol{M}_{i} \cdot
\boldsymbol{R} \cdot
\boldsymbol{Q}_{i})
\]
式(1.31) における $\boldsymbol{B}$ マトリックスは
\[\hspace{2em}
\boldsymbol{B}_{1} =
\left[
\begin{array}{ccc}
-l_{1} & -m_{1} & l_{1}(y-y_{1})-m_{1}(r-r_{1}) \\
-l_{3} & -m_{3} & l_{3}(y-y_{1})-m_{3}(r-r_{1}) \\
1/2 & 0 & (y-y_{1})/2
\end{array}
\right] \;, \;
\boldsymbol{B}_{2} =
\left[
\begin{array}{ccc}
l_{1} & m_{1} & -l_{1}(y-y_{2})+m_{1}(r-r_{2}) \\
l_{3} & m_{3} & -l_{3}(y-y_{2})+m_{3}(r-r_{2}) \\
1/2 & 0 & (y-y_{2})/2
\end{array}
\right]
\]
となるが、後の展開のため、この $\boldsymbol{B}$ マトリックを以下のように２つに分けて整理しておく。
\[\hspace{2em}
\overline{\boldsymbol{B}}_{1} =
\left[
\begin{array}{ccc}
-l_{1} & -m_{1} & l_{1}(y-y_{1})-m_{1}(r-r_{1}) \\
-l_{3} & -m_{3} & l_{3}(y-y_{1})-m_{3}(r-r_{1})
\end{array}
\right] \;, \;\;\;\;
\overline{\boldsymbol{B}}_{2} =
\left[
\begin{array}{ccc}
l_{1} & m_{1} & -l_{1}(y-y_{2})+m_{1}(r-r_{2}) \\
l_{3} & m_{3} & -l_{3}(y-y_{2})+m_{3}(r-r_{2})
\end{array}
\right]
\]
\[\hspace{2em}
\hat{\boldsymbol{B}}_{1} = [ 1/2 \;\;\: 0 \;\;\; (y-y_{1})/2 ] \;, \;\;\;\;
\hat{\boldsymbol{B}}_{2} = [ 1/2 \;\;\; 0 \;\;\; (y-y_{2})/2 ]
\]
いま、平面問題と同様、面内におけるひずみ成分を差分近似により仮定し、円周方向のひずみ成分をを加えると、以下のような相対変位とひずみの関係が得られる。
\[{\rm (1.32)}
\boldsymbol{\varepsilon} =
\left\{
\begin{array}{l}
\varepsilon_{s} \\
\varepsilon_{n} \\
\varepsilon_{\theta}
\end{array}
\right\} =
\left\{
\begin{array}{l}
\delta_{s}/h \\
\delta_{n}/h \\
\delta_{u}/r
\end{array}
\right\} \;\;\;\;
(h = h_{1} + h_{2})
\]
一方、面内変形平面要素の場合と全く同様な手順で、単位面積当たりの表面力と相対変位が以下のように関係付けられる。
\[{\rm (1.33)}
\boldsymbol{\sigma} = \boldsymbol{D} \cdot \boldsymbol{\delta}
\]
ここで、$\boldsymbol{\sigma}$ および $\boldsymbol{D}$ は、それぞれ、以下の通りで、面内変形の場合の表面力とばねの関係を示している。
\[\hspace{2em}
\boldsymbol{\sigma} = ( \tau_{s \overline{x}} \;\;
\sigma_{n} )^{t} \;\;, \;\;\;\;
\boldsymbol{D} =
\left[
\begin{array}{ccc}
k_{s \overline{x}} & 0 \\
0 & k_{n}
\end{array}
\right]
\]
また、ばね定数については、平面ひずみ状態の
式(1.17)を用いるものとする。軸対称問題の場合、これ以外に円周方向の関係、
\[{\rm (1.34)}
\sigma_{\theta} = \frac{(1-\nu)E}{(1+\nu)(1-2\nu)} \cdot \varepsilon_{\theta}
\]
を考えておく必要がある。
以上の結果から、要素境界辺上のばねに蓄えられるエネルギーを評価する。ただし、軸対称問題の場合、円周方向に蓄えられるエネルギーも評価しなければならないため、全体のエネルギーを以下に示すよう、２つの部分に分けて考える。
\[{\rm (1.35)}
V = \frac{1}{2}(\int_{l_{35}}
\boldsymbol{\overline{\delta}}^{t}
\boldsymbol{D}
\boldsymbol{\overline{\delta}} dS
+ \int_{A}
\varepsilon_{\theta} \overline{E} \varepsilon_{\theta} dA ) \times 2 \pi r
\]
ここで、
\[\hspace{2em}
\boldsymbol{\overline{\delta}} = ( \delta_{s} \;\;
\delta_{n})^{t} \;, \;\;\;\;
\overline{E} = \frac{(1-\nu)E}{(1+\nu)(1-2\nu)}
\]
である。
式(1.35) の第１項は要素境界辺上に分布するばねに蓄えられるエネルギーを表しており、先の面内変形平面要素の場合とまったく同じ結果となっている。第２項は円周方向のエネルギーで、
図1.13 に示すような積分範囲を考える。しかし、実際には簡単のため、
$\hspace{4em}$図1.13 積分範囲
\[{\rm (1.36)}
dA = \frac{h_{1}+h_{2}}{2} dS
\]
のように考え、また半径 $r$ の積分も有限要素法でよく行われているように、
\[{\rm (1.37)}
r = \frac{r_{3}+r_{4}}{2}
\]
とすることも可能である。この結果、エネルギー式は最終的に以下のように求められる。
\[{\rm (1.38)}
V = \frac{1}{2}(\boldsymbol{u}_{i}^{t}\int_{l_{34}}
\boldsymbol{\overline{B}}_{i}^{t}
\boldsymbol{D}
\boldsymbol{\overline{B}}_{i} ds \boldsymbol{u}_{i}
+ \boldsymbol{u}_{i}^{t}\int_{l_{34}}
\frac{1}{r^{2}}\boldsymbol{\hat{B}}_{i}^{t}
\overline{E}
\boldsymbol{\hat{B}}_{i} dS
\frac{h_{1}+h_{2}}{2} \boldsymbol{u}_{i} ) \times 2 \pi r
\]
このエネルギーをもとに、これまでの展開と同様にして軸対称要素の剛性行列を求めることができるが、その詳細については
9章にまとめておく。
参考までに、この軸対称要素における応力解の精度を
図1.14、
図1.15に示しておく。ただし、この要素も従来の平面要素と同様、変位の精度は若干低い。
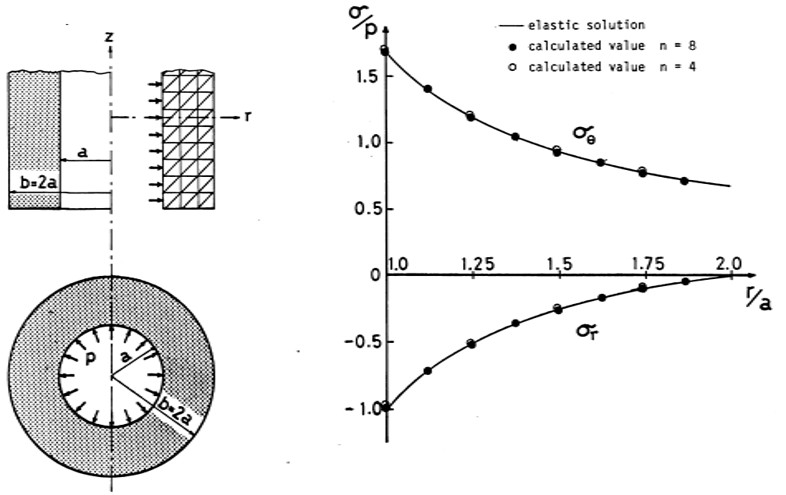
$\hspace{10em}$図1.14 内圧を受ける円筒の応力
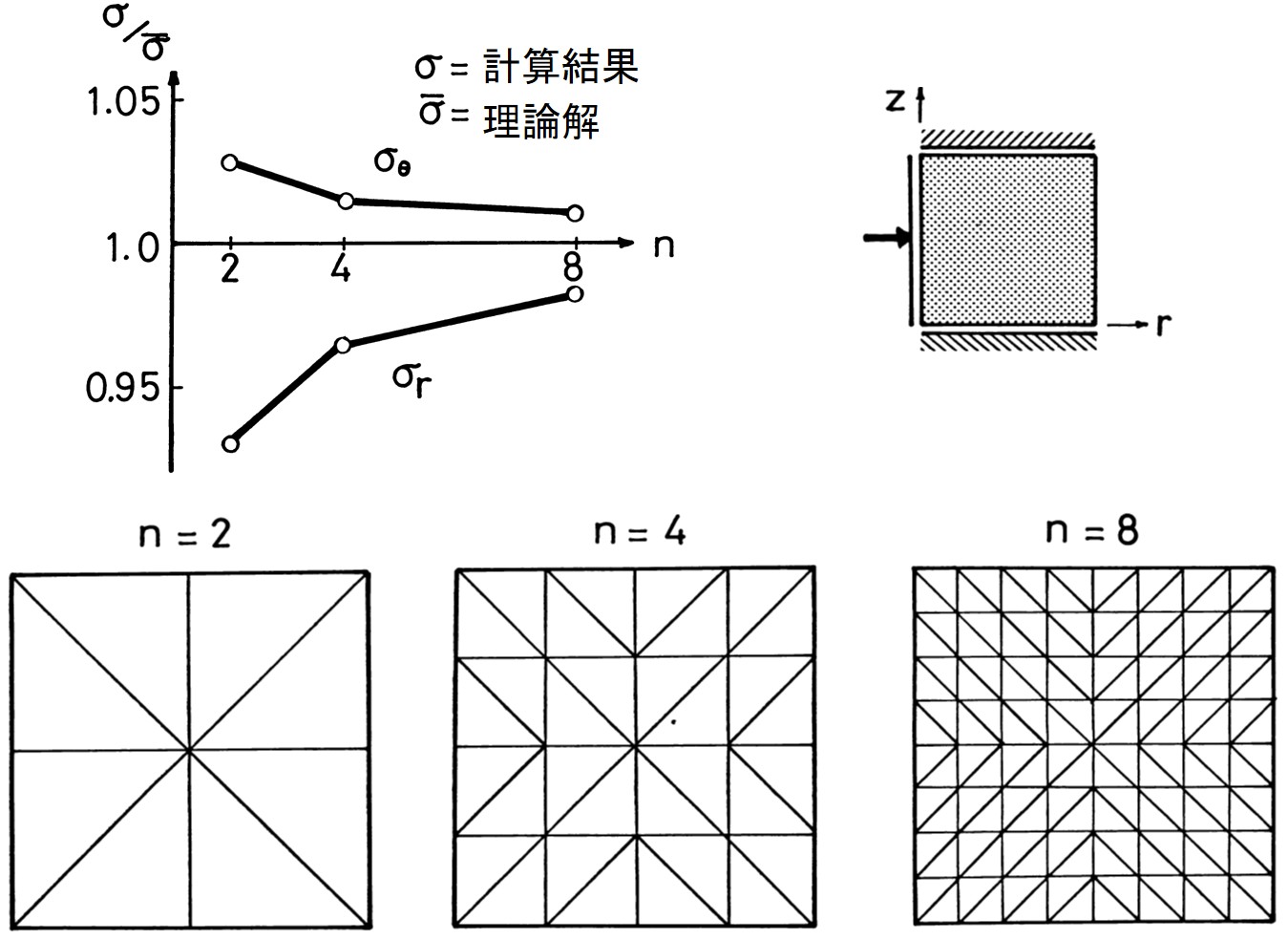
$\hspace{6em}$図1.15 応力解の精度
（５）梁要素
梁要素はアンカー、ロック・ボルトあるいは杭などを表現するため、地盤工学諸問題の解析に度々利用されている。剛体要素と梁要素では、一見異なるようにも思えるが、これまでと同様、３次元要素の特殊な場合として簡単に誘導することができる。しかも、川井モデルの梁要素と剛体要素とでは自由度が同じであるため、パラメーターの縮約などの面倒な手間をかけずに混在して利用することが可能である。都井は川井モデルの梁要素と有限要素法における梁要素の関係を積分点の相違という観点から説明している。このような方法を利用すれば明確な位置づけを行いながら梁要素の定式化を行うことができるものと思われるが、ここでは、川井モデルの立場でのみ
梁要素を考えてみる。
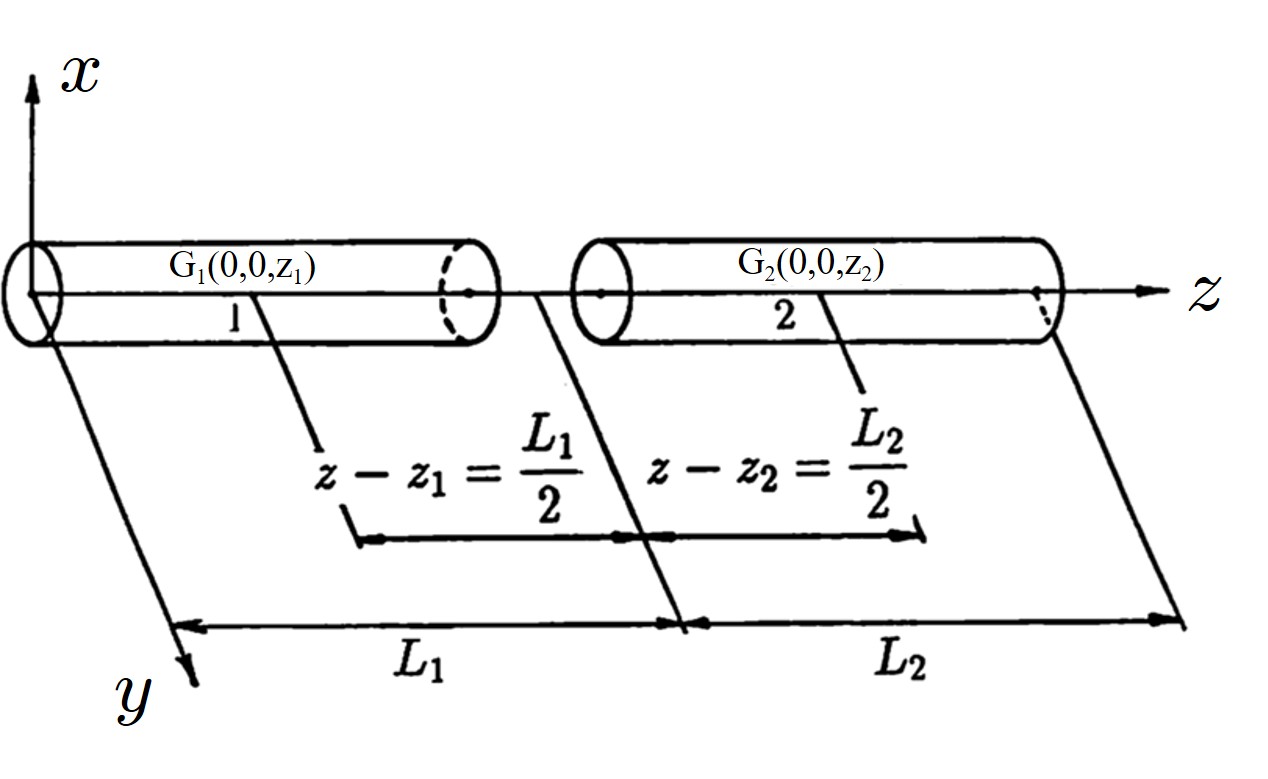$\hspace{6em}$図1.16 ３次元梁要素
３次元梁要素の定式化を行うため、
図1.16 に示すような座標系を考える。ここでは、全体座標系と局所座標系を同一に取り、$z$ 軸は部材の図心位置を通るものとしている。これより、以下の関係が得られる。
\[{\rm (1.39)}
\left.
\begin{array}{l}
l_{1} = m_{1} = 0 \;, \;\;\; n_{1} = 1 \\
l_{2} = m_{2} = 0 \;, \;\;\; n_{2} = 1 \\
l_{3} = m_{3} = 0 \;, \;\;\; n_{3} = 1 \\
x_{1} = x_{2} = y_{1} = y_{2} = 0 \\
z-z_{1} = L_{1}/2 \;, \;\;\; z-z_{2} = L_{2}/2
\end{array}
\right\}
\]
したがって、接触面上の任意点における変位ベクトルは
\[{\rm (1.40)}
\boldsymbol{U}_{i} = \boldsymbol{Q}_{i} \cdot \boldsymbol{u}_{i}
\]
と表すことができる。ここで、それぞれの行列の成分は以下に示す通りである。
\[\hspace{2em}
\boldsymbol{U}_{1} = ( U_{1} \;\; V_{1} \;\; W_{1} )^{t} \;\;\;\;
\boldsymbol{U}_{2} = ( U_{2} \;\; V_{2} \;\; W_{2} )^{t}
\]
\[\hspace{2em}
\boldsymbol{u}_{1} = ( u_{1} \;\; v_{1} \;\; w_{1} \;\;
\theta_{1} \;\; \phi_{1} \;\; \chi_{1} )^{t} \;\;\;\;
\boldsymbol{u}_{2} = ( u_{2} \;\; v_{2} \;\; w_{2} \;\;
\theta_{2} \;\; \phi_{2} \;\; \chi_{2} )^{t}
\]
\[\hspace{2em}
\boldsymbol{Q}_{1} =
\left[
\begin{array}{cccccc}
1 & 0 & 0 & 0 & L_{1}/2 & -y \\
0 & 1 & 0 & -L_{1}/2 & \; 0 & \; x \\
0 & 0 & 1 & y & -x & \; 0
\end{array}
\right] \;, \;\;\;\;
\boldsymbol{Q}_{2} =
\left[
\begin{array}{cccccc}
1 & 0 & 0 & 0 & L_{2}/2 & -y \\
0 & 1 & 0 & -L_{2}/2 & \; 0 & \; x \\
0 & 0 & 1 & y & -x & \; 0
\end{array}
\right]
\]
２要素間の相対変位は、局所座標と全体座標が一致しているため、座標変換を行わずに直接以下のようにして求めることができる。
\[{\rm (1.41)}
\boldsymbol{\delta} = \sum_{i=1}^{2}
\boldsymbol{M}_{i} \cdot \boldsymbol{U}_{i}
= \sum_{i=1}^{2}
\boldsymbol{M}_{i} \cdot
\boldsymbol{Q}_{i} \cdot
\boldsymbol{u}_{i}
\]
ただし、$\boldsymbol{\delta}$ および $\boldsymbol{M}$ は以下の通りである。
\[\hspace{2em}
\boldsymbol{\delta} = ( \delta_{sx} \;\;
\delta_{sy} \;\;
\delta_{n} )^{t}
\]
\[\hspace{2em}
\boldsymbol{M}_{1} =
\left[
\begin{array}{rrr}
-1 & 0 & 0 \\
0 & -1 & 0 \\
0 & 0 & -1
\end{array}
\right] \;, \;\;\;\;
\boldsymbol{M}_{2} =
\left[
\begin{array}{ccc}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1
\end{array}
\right]
\]
一方、単位面積当たりの表面力と相対変位の関係は
\[{\rm (1.42)}
\boldsymbol{\sigma} = \boldsymbol{D} \cdot \boldsymbol{\delta}
\]
で与えられるものと仮定する。ここで、$\boldsymbol{\sigma}$ は単位面積当たりの表面力で
\[\hspace{2em}
\boldsymbol{\sigma} = ( \tau_{sx} \;\;
\tau_{sy} \;\;
\sigma_{n} )^{t}
\]
なる関係がある。また、$\boldsymbol{D}$ はばね行列でこれまでと同様、以下のような関係があるものとする。
\[\hspace{2em}
\boldsymbol{D} =
\left[
\begin{array}{ccc}
k_{sx} & 0 & 0 \\
0 & k_{sy} & 0 \\
0 & 0 & k_{n}
\end{array}
\right]
\]
ただし、ばね定数はポアソン比の影響を無視し、以下のように考える。
\[\hspace{2em}
k_{sx} = k_{sy} = \frac{G}{L_{1}+L_{2}} \;, \;\;\;
k_{n} = \frac{E}{L_{1}+L_{2}}
\]
以上の準備のもと、これまでの展開と同様な手順により梁の剛性行列を誘導することができる。ただし、梁要素の場合、接触面が三角形とは限らないため、積分の考え方が若干異なる。この点を含め、３次元梁要素の剛性行列を
9章にまとめておく。
２次元の場合も、これらの関係をさらに簡略化することで、軸剛性、曲げ剛性、ねじり剛性などの各種の剛性行列を簡単に求めることができる。この結果は
9章に示してある。
次に、梁要素の利用方法について説明しよう。
図1.16 より想像できると思うが、直線的に配置された２つの梁のみを取り上げ、図心軸と全体座標系を一致させ説明を行ってきた。しかし、実際の構造は、このように直線だけで表現することはできない。例えば、
図1.17(a) に示すよう、構造座標系に対し傾斜して配置されていたり、
図(b)のように接合部があったりする。
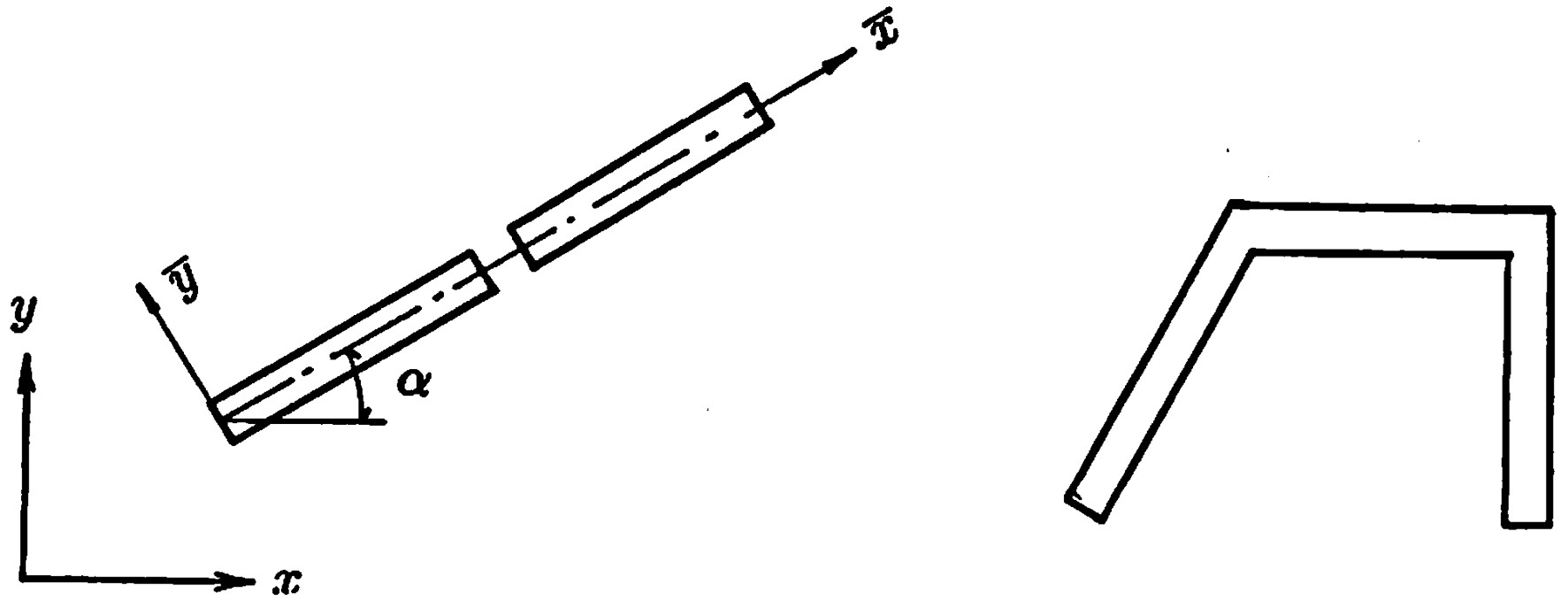$\hspace{7em}$(a) $\hspace{11em}$(b)
$\hspace{7em}$図1.17 一般的は梁部材の配置
前者については、通常の骨組み構造解析と同様、一旦得られた部材剛性行列を座標変換し、構造座標系に置き換えて全体剛性行列に組み込めばよい。後者の場合は、やや面倒である。まず、
図1.18 に示すよう、２つの部材の間に自由度だけがあり、質量も長さも持たないピン要素を考える。
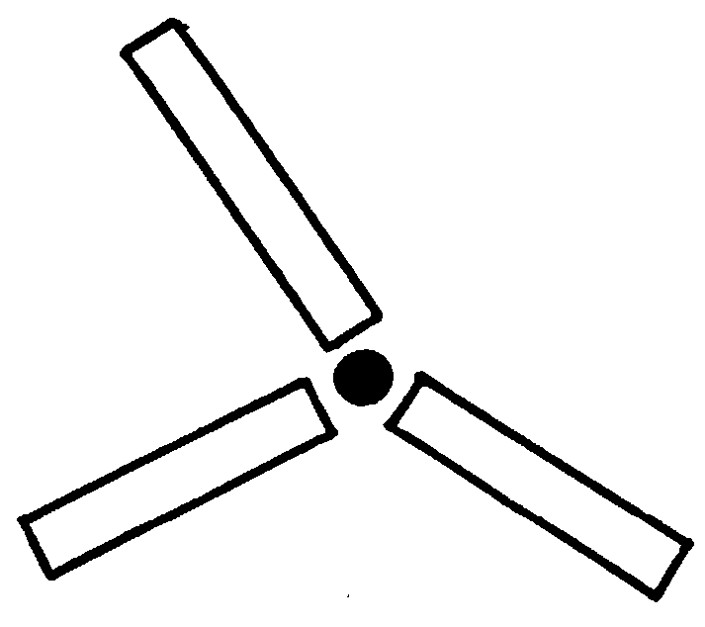
$\hspace{0em}$図1.18 ピン要素
このピン要素と各梁要素に対して、それぞれ、部材剛性行列を作成し、先の傾斜して配置された梁要素と同様、座標変換を行って全体剛性行列に組み込む。この考え方は、データーの作成が面倒となる反面、
6章で説明する要素の追加、削除が簡単に行えるため、施工段階の解析が簡単に行えるというメリットもある。もちろん、ピン要素の自由度を縮約することも可能であるが、プログラムを一般的に組むことができなくなるのであまり勧められない。
土や岩盤の破壊は数多くの要因によって引き起こされる。これらの要因をすべて考慮し安定解析や応力解析を行うことは至難の業であり、実験あるいは計算機の性能を考え合わせると殆ど不可能である。特に、解析的手法を用いる場合はあらゆる条件とは言わないまでも、現在よく知られている二三の条件を取り入れて一般的な解を得ることさえ困難である。しかし、地盤の定性的な破壊や変形の状況を理解しようとするなら、代表的な要因を幾つか取り込むことでも実用的な解を得ることが可能であろう。地盤などの問題では、いまだ不明確な点が多く、実験的あるいは理論的研究が盛んに行われている現状では、工学的判断を無視したシミュレーションは考えられない。
さて、代表的な地盤の破壊形態としてせん断破壊を上げることができる。地盤に許容値以上の荷重が上部構造を通じて加わったり、土自身の重さによって大きな荷重を受けたとき、土はすべり破壊、すなわち、せん断破壊が生ずる。これによって構造物に不等沈下や転倒が生じ、極めて危険な状態になる。また、斜面などでは地滑りや崩落が発生し多大な被害をもたらすことも希ではない。このような危険な状態が発生しないよう安全性を確保するためには破壊の生ずる面や荷重を予想し、予め対策を講じておく必要があり、この目的のため
安定解析や
極限解析がよく利用されている。
安定問題に関する数値実験を行う際に問題となるのが破壊規準である。現在、実験技術の進歩とともに多くの実験式的破壊規準が提案されており、今後引き続き発展してゆくであろう。しかし、どの方法によってもあらゆる問題に適用できる式は現在のところなく、問題に応じて破壊規準を選択するのが適切であろう。本書は破壊規準をどのように定義するかという観点よりも、与えられた破壊規準を離散化極限解析にいかに取り込むかという点に主眼を置いている。そこで、ここでは代表的な幾つかの破壊条件を例にとり構成式の取扱いを中心に説明する。
土の場合、破壊規準の代表的な考え方として
Su法（φ＝０法）と
Cφ法がある。Su法はせん断強さが非排水強度 $C_u$ で決まるものとして安定解析を行う方法で、$\phi=0^{\circ}$ とすることから
φ＝０法とも呼ばれている。もちろん、不飽和土についても非排水強度を用いれば同じことがいえるが、実際に不飽和土の非排水強度を求めることは困難である。これに対し、 Cφ法というのは有効応力とせん断強度の間に一次結合のようなある一定の条件を用いて安定解析を方法である。前者を
全応力解析法、後者を
有効応力解析と呼ぶこともある｡
塑性論の立場から考えると Suu法はトレスカの条件に相当する考え方で、
最大せん断応力説に基づいてする。すなわち、最大せん断応力がある固有な値に達すると破壊が生ずるという考え方である。一方、Ｃφ法はクーロンの説に基づく方法と対応している。これは、
修正最大せん断応力説の一つで
内部摩擦説とも呼ばれている。一方、モールがさらに一般的な方法として応力円の包絡線を用いて説明している。の包絡線を簡単な直線と考えればクーロンの説と同様な式が得られる。このことから、クーロンの説を
モール・クーロンの説と呼ぶこともある。
さて、川井モデルでは要素境界面上における単位面積当たりの表面力を扱っている。したがって、要素間のすべりを表現する破壊条件式は合力で与えられる式をそのまま使用することになる。この点が主応力を扱う従来の有限要素法と大きく異なる点の１つである。表面力がベクトル量であることを考えるとこのことは当然であろう。
図1.19に代表的な破壊条件を示す。
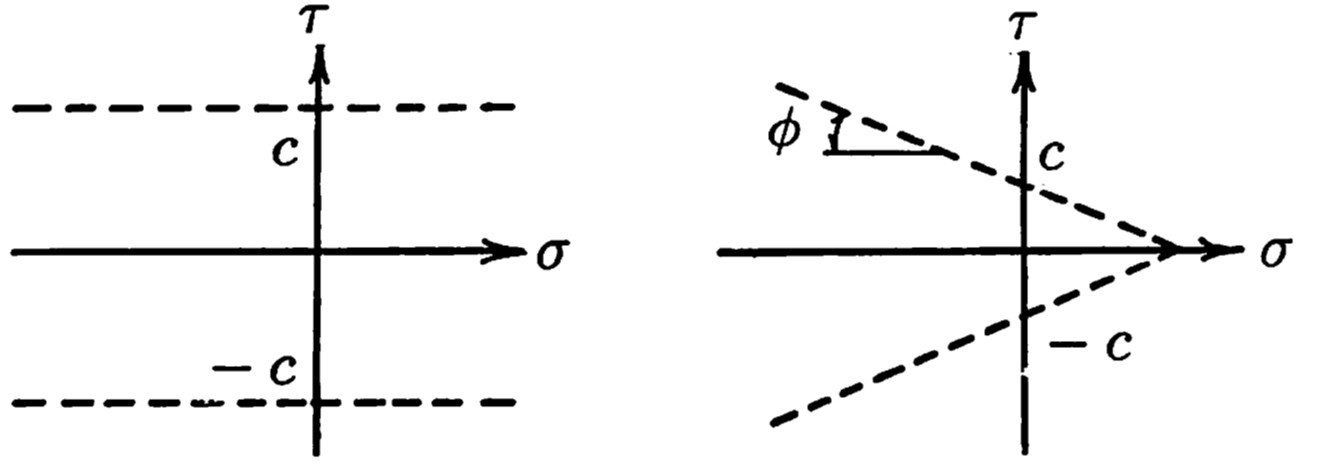
$\hspace{1em}$(a) トレスカの条件$\hspace{2em}$(b) モール・クーロンの条件
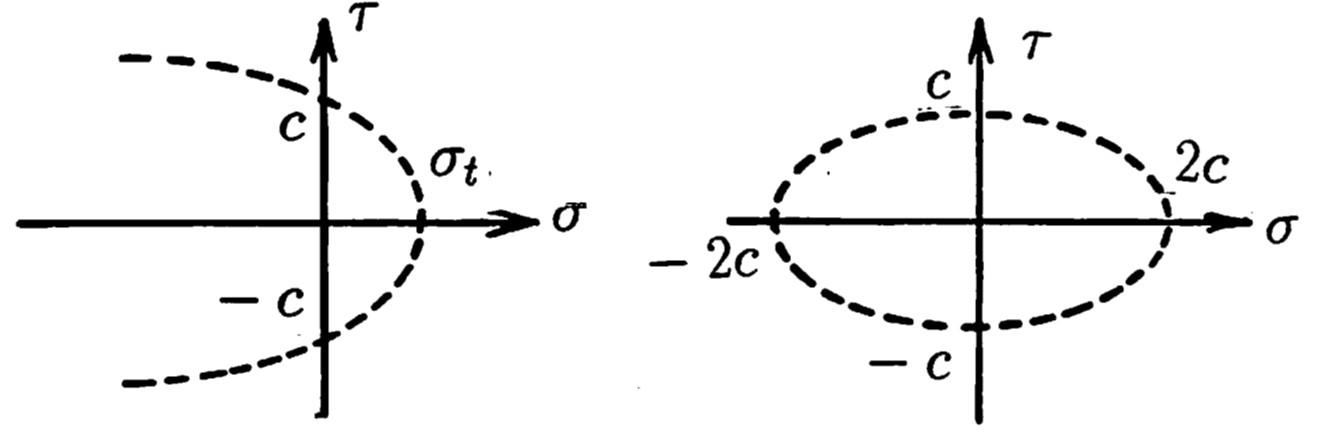
$\hspace{1em}$(c) モールの条件$\hspace{5em}$(d) ミーゼスの条件
$\hspace{5em}$図1.19 各種の破壊条件
図1.19(a)には
トレスカの条件、すなわち、Su法に対する破壊条件が示されている。この場合、
塑性ポテンシャルは
（トレスカの条件）
\[{\rm (1.43)}
f = \tau^{2} - c^{2}
\]
となる。２次元問題の場合、川井モデルによって得られる単位面積当たりの表面力は $(\sigma_n, \tau)$ であるため、
式(1.43) をそのまま利用すればよい。また、３次元問題の場合は、$(\sigma_n, \tau_{sx}, \tau_{sy})$ が求められるため、
\[{\rm (1.44)}
\tau^{2} = \tau_{s\overline{x}}^{2} + \tau_{s\overline{y}}^{2}
\]
のように、せん断力に対する合力を考え、
式(1.43) を適用する。この後示す他の破壊条件に対しても、
式(1.44) の関係を利用すれば３次元問題に対しても利用することができる。
図1.19(b)は
モール・クーロンの条件に対するもので、この場合の塑性ポテンシャルは以下のようになる。
（モール・クーロンの条件）
\[{\rm (1.45)}
f = \tau^{2} - (c-\tan\phi \cdot \sigma_{n})^{2}
\]
この一般的な形であるモールの条件が
図1.19(c)に示されている。もし、この包絡線が放物線であるなら、塑性ポテンシャルは以下のようになる。
（モールの条件：放物線包絡線）
\[{\rm (1.46)}
f = \tau^{2} - c^{2}(1-\frac{\sigma_{n}}{\sigma_{t}})
\]
また、地盤の応力解析ではあまり利用されないが、
ミーゼスの条件についても
図1.19(d)に示しておく。この条件に対する塑性ポテンシャルは
（ミーゼスの条件）
\[{\rm (1.47)}
f = \tau^{2} + \frac{1}{4}\sigma_{n}^{2} - c^{2}
\]
で与えられる。
以上の破壊条件は３次元や面内変形平面問題の場合に適用される。次に軸対称問題の場合について考えてみよう。
1.2節でも説明したように、川井モデルにおける軸対称要素では円周方向の応力と面内の表面力とに関連性を持たせていないため、有限要素法における考え方と若干異なる。川井モデルにおける軸対称要素を用いた場合の最も単純な破壊条件の考え方は、面内と円周方向を分離し、面内については先に示したトレスカの条件やモール・クーロンの条件などを、また、円周方向については別途以下の関係を利用する。
\[{\rm (1.48)}
f = \sigma_{\theta} - \sigma_{t}
\]
この式では円周方向の応力が許容引っ張り応力を越えたら破壊したものと考えている。この関係が適切かについてはまだ若干の検討の余地がある。
川井モデルにおける梁要素の降伏条件については、従来の骨組構造解析の場合とまったく同様である。ここでは、参考までに２次元の場合に対する例を示しておく
\[{\rm (1.49)}
f = \left( \frac{M}{M_{px}} \right)^{2}
+ \left( \frac{F_{y}}{F_{py}} \right)^{2}
+ \left( \frac{P}{P_{y}} \right)^{2}
- 1
\]
ここで、$M_{px}$ は全塑性曲げモーメント、$F_{py}$ は全塑性せん断力、$P_y$ は全塑性軸力である。ただし、この式は説明のための式で、あまり現実的ではない。実際に解析で使用する場合は適切な破壊条件式を用いなければならない。
さて、以上のようにして求まった降伏条件や塑性ポテンシャルを用いて離散化極限解析を行うためには、塑性化後の構成式を誘導しておく必要がある。以下にその誘導方法を簡単にまとめておく。
いま、塑性ポテンシャル $f$ を
\[{\rm (1.50)}
f( \boldsymbol{\sigma}) = 0 \;\;\;\;\;
\boldsymbol{\sigma} = ( \sigma_{n} \;, \; \tau )
\]
と表せば、
塑性流れ則に従い、次の関係が得られる。
\[{\rm (1.51)}
\Delta \boldsymbol{\epsilon} ^{(p)} =
\lambda \frac{\partial f}{\partial \boldsymbol{\sigma}} \;\;\;\;\;
\boldsymbol{\varepsilon} ^{(p)} = ( \varepsilon_{n}^{(p)} \;, \; \gamma^{(p)} )
\]
ここで、上付きの $(p)$ は塑性状態の量であることを意味する。弾性状態の量を $(e)$ で表せば、全ひずみ $(\boldsymbol{\varepsilon})$ に対して以下のような関係が得られる。
\[{\rm (1.52)}
\Delta \boldsymbol{\varepsilon} ^{(e)} =
\Delta \boldsymbol{\varepsilon} -
\Delta \boldsymbol{\varepsilon} ^{(p)}
\]
ここで、$\Delta$ は増分形式であることを意味する。
さて、弾性時における応力とひずみ（川井モデルの場合、単位面積当たりの表面力と単位長さ当たりの相対変位）の間には次の関係が成立する。
\[{\rm (1.53)}
\boldsymbol{\sigma} = \boldsymbol{K}^{e} \cdot
\Delta \boldsymbol{\varepsilon} ^{(p)}
\]
したがって、
式(1.51)～
式(1.53)を整理することで以下の関係が得られる。
\[{\rm (1.54)}
\Delta \boldsymbol{\sigma} = \boldsymbol{K}^{e}(
\Delta \boldsymbol{\varepsilon} -
\lambda \frac{\partial f}{\partial \boldsymbol{\sigma}} )
\]
さらに、この関係を
塑性条件
\[{\rm (1.55)}
\frac{\partial f}{\partial \boldsymbol{\sigma}}
\Delta \boldsymbol{\sigma} = 0
\]
に代入し $\lambda$ について解くと以下の関係が得られる。
\[{\rm (1.56)}
\lambda = \frac{\boldsymbol{K}^{(e)}
\displaystyle \frac{\partial f}{\partial \boldsymbol{\sigma}}
\Delta \boldsymbol{\varepsilon}}
{\displaystyle \frac{\partial f}{\partial \boldsymbol{\sigma}}
\boldsymbol{K}^{(e)}
\frac{\partial f}{\partial \boldsymbol{\sigma}}}
\]
この関係を
式(1.54)に代入すれば、最終的に以下のような増分表面力の関係式が得られる。
\[{\rm (1.57)}
\Delta \boldsymbol{\sigma} =
\left[
\boldsymbol{K}^{(e)} -
\frac{ \displaystyle
\boldsymbol{K}^{(e)}
\frac{\partial f}{\partial \boldsymbol{\sigma}}
\frac{\partial f}{\partial \boldsymbol{\sigma}}
\boldsymbol{K}^{(e)}
}
{ \displaystyle
\frac{\partial f}{\partial \boldsymbol{\sigma}}
\boldsymbol{K}^{(e)}
\frac{\partial f}{\partial \boldsymbol{\sigma}}
}
\right]
\Delta \boldsymbol{\varepsilon}
\]
なお、この式にはひずみ硬化などの影響は含まれていない。上式は、いわゆる、破壊条件に対する表面力と相対変位の比例関係のような扱いとなっている。この式を基に塑性化後の構成式を誘導し、成分により表示すると
\[{\rm (1.58)}
k_{ij}^{(p)} = k_{i}^{(e)} \delta_{ij} -
\frac{1}{\sum_{i}^{ }k_{i}^{(e)}\overline{f}_{i}^{2}}
\overline{f}_{i} \overline{f}_{j} k_{i}^{(e)} k_{j}^{(e)}
\]
と表すことができる。ここで、
\[
\overline{f}_{i} =
\frac{\partial f}{\partial \sigma_{i}} \;\;\;\;\;
\sigma_{i} = ( \sigma_{n} \;, \; \tau )
\]
である。また、$k_i^{(e)}$ は弾性時におけるばねの対角成分を表している。なお、塑性解析における除荷の判定は塑性仕事から求めるべきであるが、便宜上
\[{\rm (1.59)}
\lambda \lt 0
\]
より判定してもかまわない。
先に示した破壊条件に対する具体的な塑性化後の構成式については
9章にまとめておく。