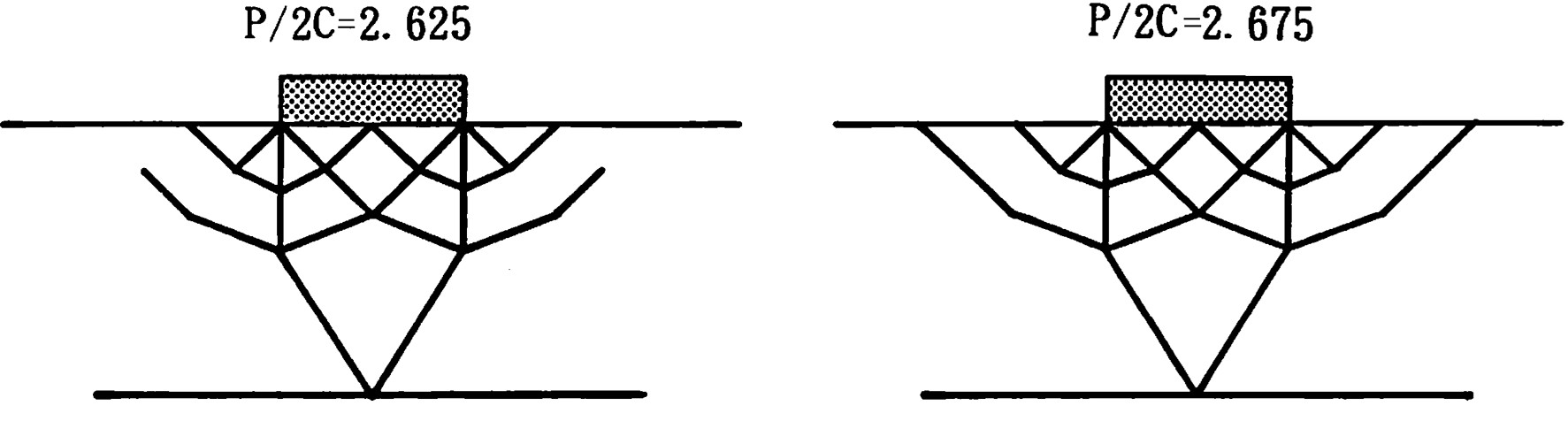土や岩盤の応カーひずみ関係を調べてみると、ほとんどの場合、非線形挙動を示しており、このことが地盤の応力解析を複雑なものとしている原因の一つとなっている。応カーひずみ関係が非線形であれば、それを利用して作成される剛性方程式も、当然、非線形となるため、何らかの近似解法が必要となる。このような材料非線形問題の有限要素法による計算法についてはこれまで数多くの研究が発表されてきた。基本的には代数方程式の解法であるため、どのような方法を用いても解析可能であろうが、それぞれに長所、短所があり、常に好ましい結果が得られるとは限らない。解法によってはある特定の構成式に適したものもあるであろうし、使用するモデルによってはあまり得策ではない場合もある。また、同じ非線形問題であったとしても非線形性の強い場合と弱い場合とでは扱いが異なる。当然、非線形代数方程式の近似解法であるため各種の誤差も発生するであろう。本章ではこのような材料非線形問題の解法について説明を行うが、その前に、前提となる応カーひずみの関係を整理しておこう。
図3.1は代表的な3タイプの応カーひずみ関係を示した図である。
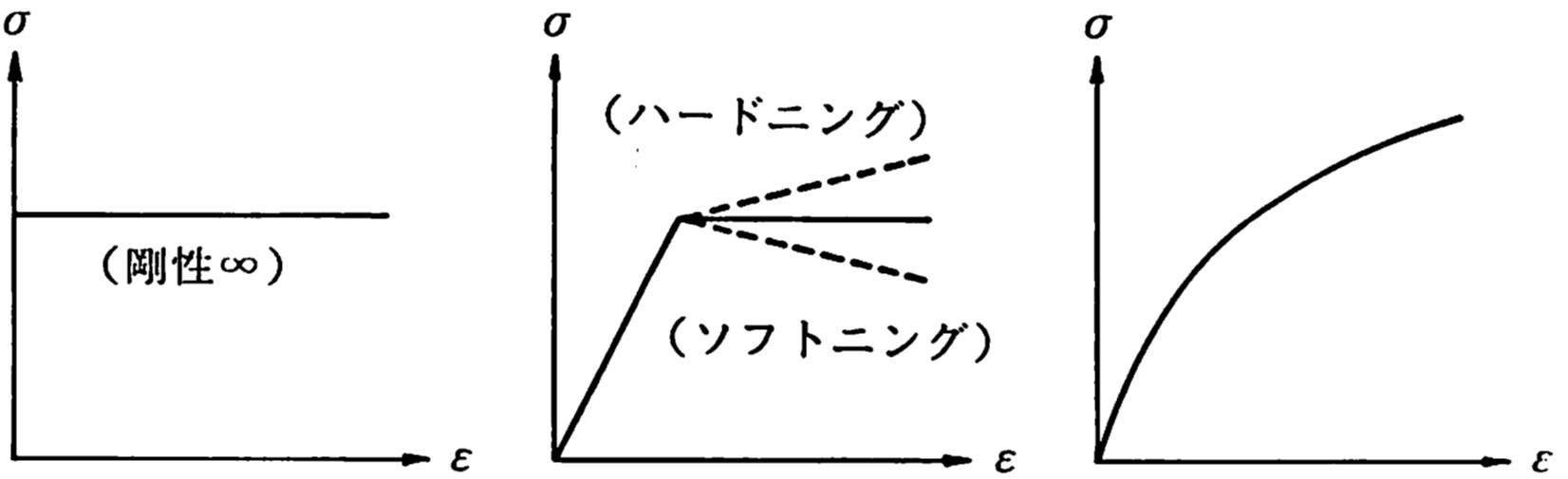
$\hspace{1em}$(a)剛塑性タイプ$\hspace{2em}$(b)完全弾塑性タイプ
$\hspace{1em}$(c)一般タイプ
$\hspace{4em}$図3.1 モデル化された応力ーひずみ関係
図(a)に示した
剛塑性タイプの関係は
塑性解析に利用されており、変形係数を無限大と仮定している。このため、有限要素法やRBSMのように変形から応力を求める変位型の解法ではこのような関係を単純に利用することはできない。
図(b)は
完全弾塑性タイプの場合で、とりあえず図中の点線で示されているような直線で表されるハードニングやソフトニングも含まれるものとする。数値計算上は、
図3.2に示されるような折れ線によって表される応カーひずみ関係も後述する理由により、この
図(b)に含まれるものとする。
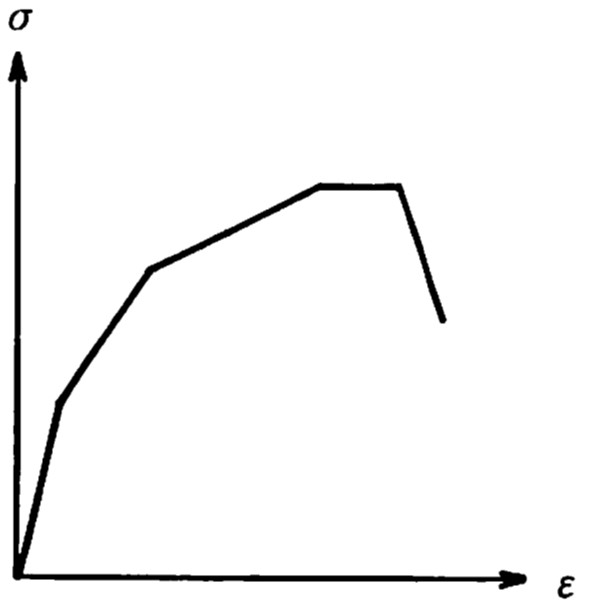
$\hspace{0em}$図3.2 折れ線で近似された応力ーひずみ関係
図(b)の関係は、ある意味で極端に理想化された応カーひずみ関係とみなすことができるが、土のような粒状体から構成される材料では、マクロ的に眺めた場合、
図(C)のように明確な降伏点が得られないのが一般的である。
図(b)と
図(C)とでは、非線形解法の取り扱いに相違が生ずる場合もあるため、ここでは、初めに
図(C)の一般的タイプに対する解法について説明し、次いで
図(b)のようなタイプに対する追加説明を行うことにする。
非線形解析法を大まかに整理すると、以下に示すの3つの基本的な方法に分類できる。
- 1) 荷重増分法
- 2) 反復法
- 3) 混合法((1)と(2)を組み合わせたという意味での)
ただし、ここで 使用した表現は代表的なものであり、分類法そのものについても若千の相違はあるかもしれない。例えば、
可変剛性法と
等価荷重法といった2つに分類しているものもある。
荷重増分法は目的とする荷重を適切な増分荷重に分割し、各荷重増分段階毎に剛性を変化させながら計算する方法で、増分荷重が作用している間は剛性を一定として線形計算を行う。この方法には
(荷重増分法)
などがある。
一方、
反復法は目的とする全荷重を作用させ、解を修正してゆく方法であり、剛性を変化させる方法とそうでなものがある。代表的な方法には
(反復法)
- ・直接反復法(割線係数法)
- ・Newton-Raphdon法
- ・修正Newton-Raphdon法
などかある。初めの2つが剛性を修正する方法で、3番目が初期剛性を利用する方法である。2章で説明した応力遷移法は、この反復法に含まれる。
反復法では、はじめに仮定した応カーひずみ関係と計算による値を比較し不適切な応力もしくはひずみを修正しなければならない。この方法として以下の 2つの考え方がある。
(反復法における修正法)
ただし、分類の方法が異なれば、その位置付けも異なってくる。
また、
混合法は荷重増分法と反復法の特徴を組み合わせた方法であり、
step-iteration法とも呼ばれている。代表的な方法として、修正Newton-Raphson法と組み合わせた方法が提案されている。
本節では荷重増分法の一般的な手順について説明し、次いでその長所と短所を整理し、RBSMによる離散化極限解析に適用する上での注意事項を述べる。
一般的な荷重増分法では、与えられた応カーひずみ関係の非線形性の強さに応じて全体の荷重を幾つかの小さな増分荷重に分割する。次に、この分割された増分荷重を作用させ、線形解析を行う。その結果得られた変位や応力を前回までの変位や応力に次のように重ね合わせる。
\[{\rm (3.1)}
\left.
\begin{array}{lcr}
\boldsymbol{u}^{n+1} &=& \Delta \boldsymbol{u}^{n+1}
\displaystyle + \sum_{i=1}^{n} \Delta \boldsymbol{u}^{i} \\[0.5em]
\boldsymbol{\sigma}^{n+1} &=& \Delta \boldsymbol{\sigma}^{n+1}
\displaystyle + \sum_{i=1}^{n} \Delta \boldsymbol{\sigma}^{i}
\end{array}
\right\}
\]
ここで、$\boldsymbol{u}^{n+1}$ あるいは $\boldsymbol{\sigma}^{n+1}$ は(n + 1)番目の増分荷重が作用し終わったときの全変位および全応力を示しており、$\Delta \boldsymbol{u}^i$ あるいは $\Delta \boldsymbol{\sigma}^i$ は $i$ 番目の増分荷重が単独で作用したときの増分変位あるいは増分応力である。
荷重増分法では、各増分荷重の作用中に剛性を変化させないという前提により線形解析を可能にしており、非線形性の導入は、次の増分荷重による解析に移る直前に行われる。ところが、
図3.1(c)のように応カーひずみ関係が曲線で表される材料の場合、剛性が連続的に変化しているため、剛性決定にあたり、何らかの近似が必要となる。
この剛性の決定法として、一般的によく利用されているのが、
接線剛性を用いる方法である。
図3.3は各応カレベルでの接線剛性を示した図である。
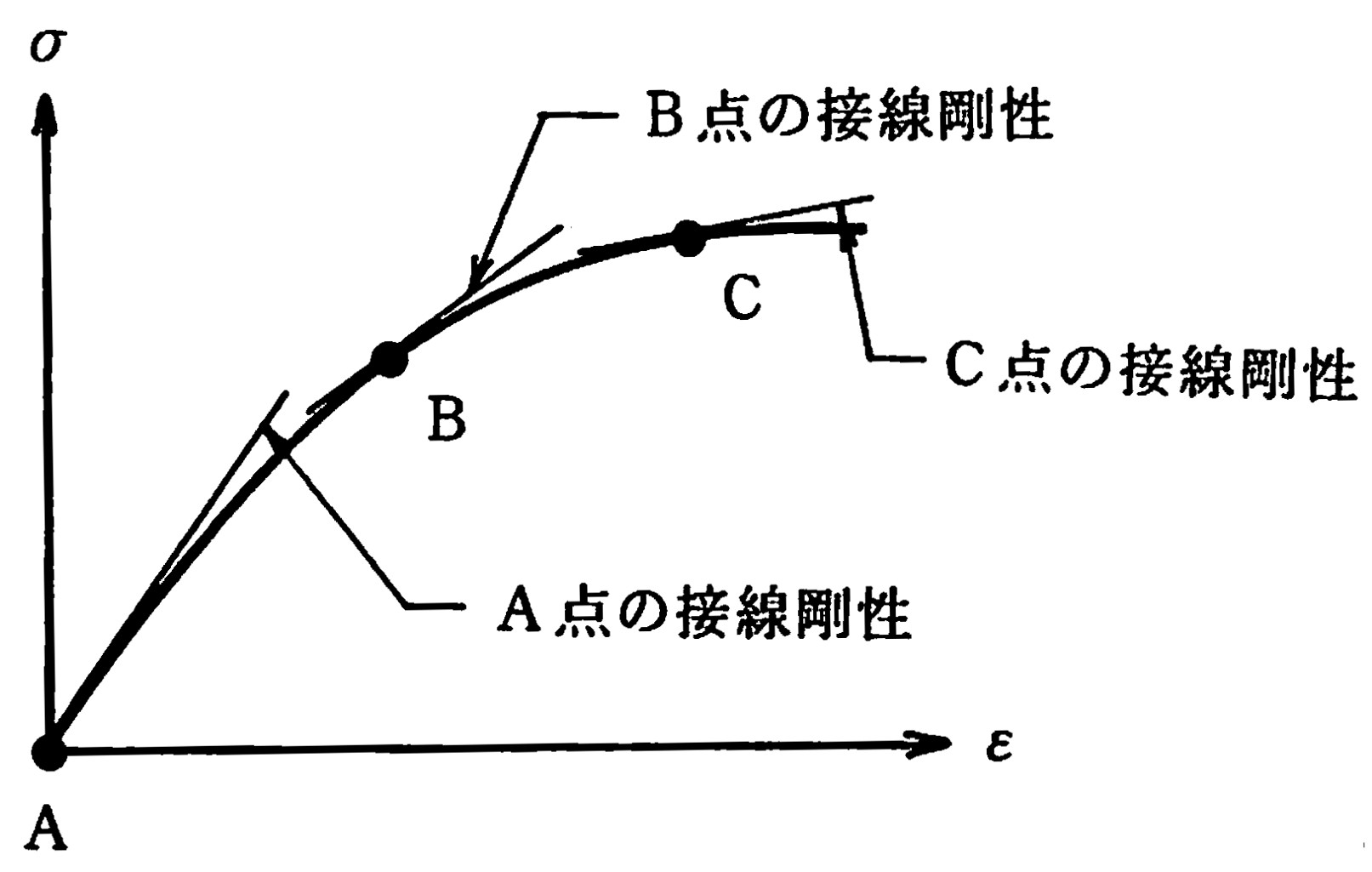 $\hspace{4em}$図3.3 接線剛性
$\hspace{4em}$図3.3 接線剛性
この図を眺めてみると、荷重増分法により一見正しく解が求められるように見受けられるが、実際には、
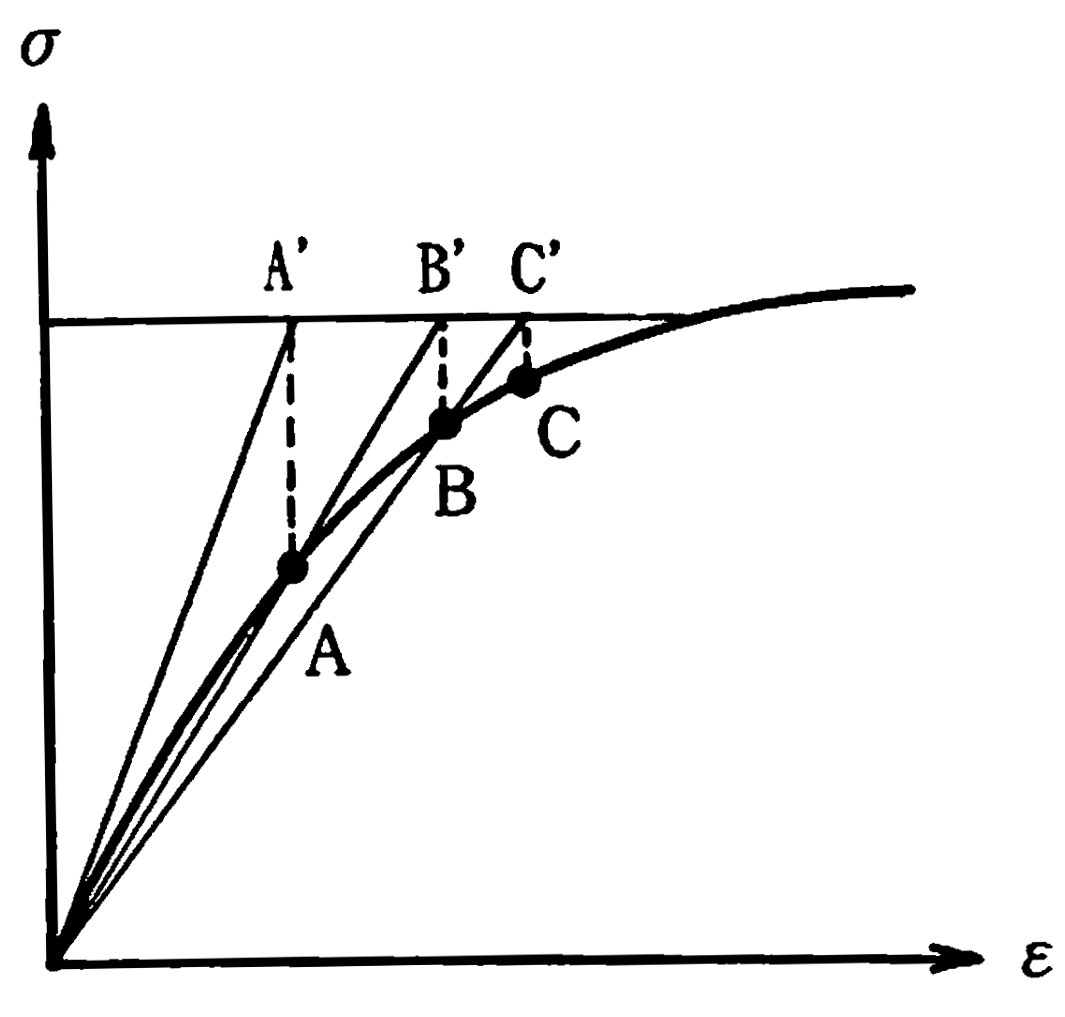
図3.4に示すよう、荷重増分回数の増加とともに誤差が累積してゆく。
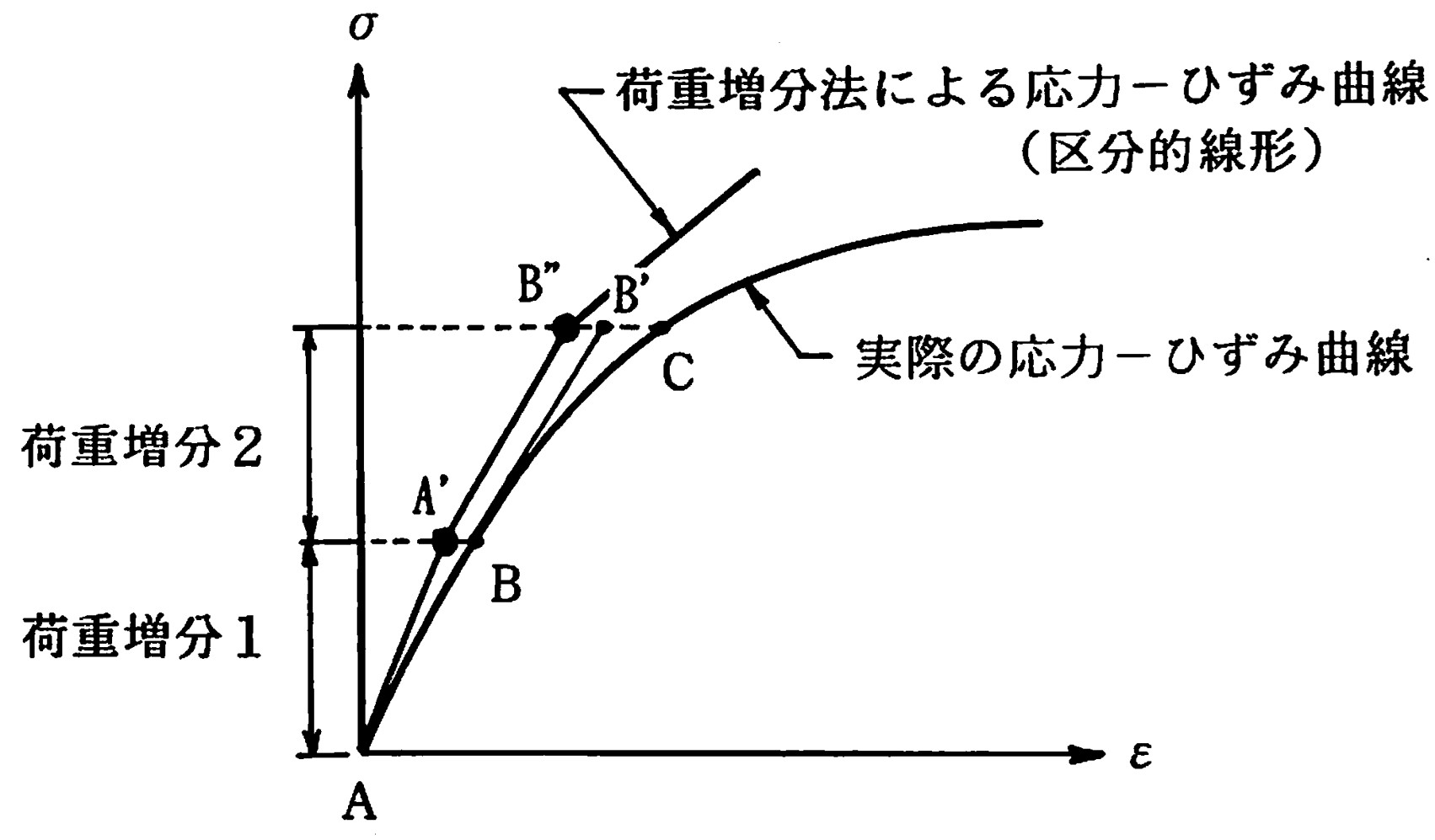
$\hspace{2em}$図3.4 荷重増分法の応力ーひずみ曲線
図からも理解できるように、荷重増分法ではA点の接線剛性を用いて荷重増分1を作用させることで線形解析を行う。したがって、B点の応力とひずみではなくA'点の応力とひずみが得られる。同様に、荷重増分2の段階ではB点の接線剛性を用いるため、B点を基準に考えるとC点ではなくB'点の値が求まる。しかし、実際には
式(3.1)のような重ね合わせを行うため、荷重増分2が作用し終わった段階ではB”点での応力とひずみが得られる。したがって、荷重増分量を無限に小さくしてゆけば正解に近づくが、数値計算上それは現実的ではないため、誤差が累積する。この方法は接線剛性を利用することから、
接線剛性法あるいは
接線係数法とも呼ばれている。
オイラー法は、このようにして決定された性を利用し、
\[{\rm (3.2)}
\boldsymbol{K}^{n} \cdot \Delta \boldsymbol{u}^{n+1} = \Delta \boldsymbol{F}^{n+1}
\]
を解く最も単純な方法である。ここで、$\boldsymbol{K}^{n}$ は前回の応カレベルにおける接線剛性を用いていることを示している。
一方、誤差の累積を減らすため、
図3.5に示すような
Runge-Kutta法を利用した荷重増分法も提案されている。
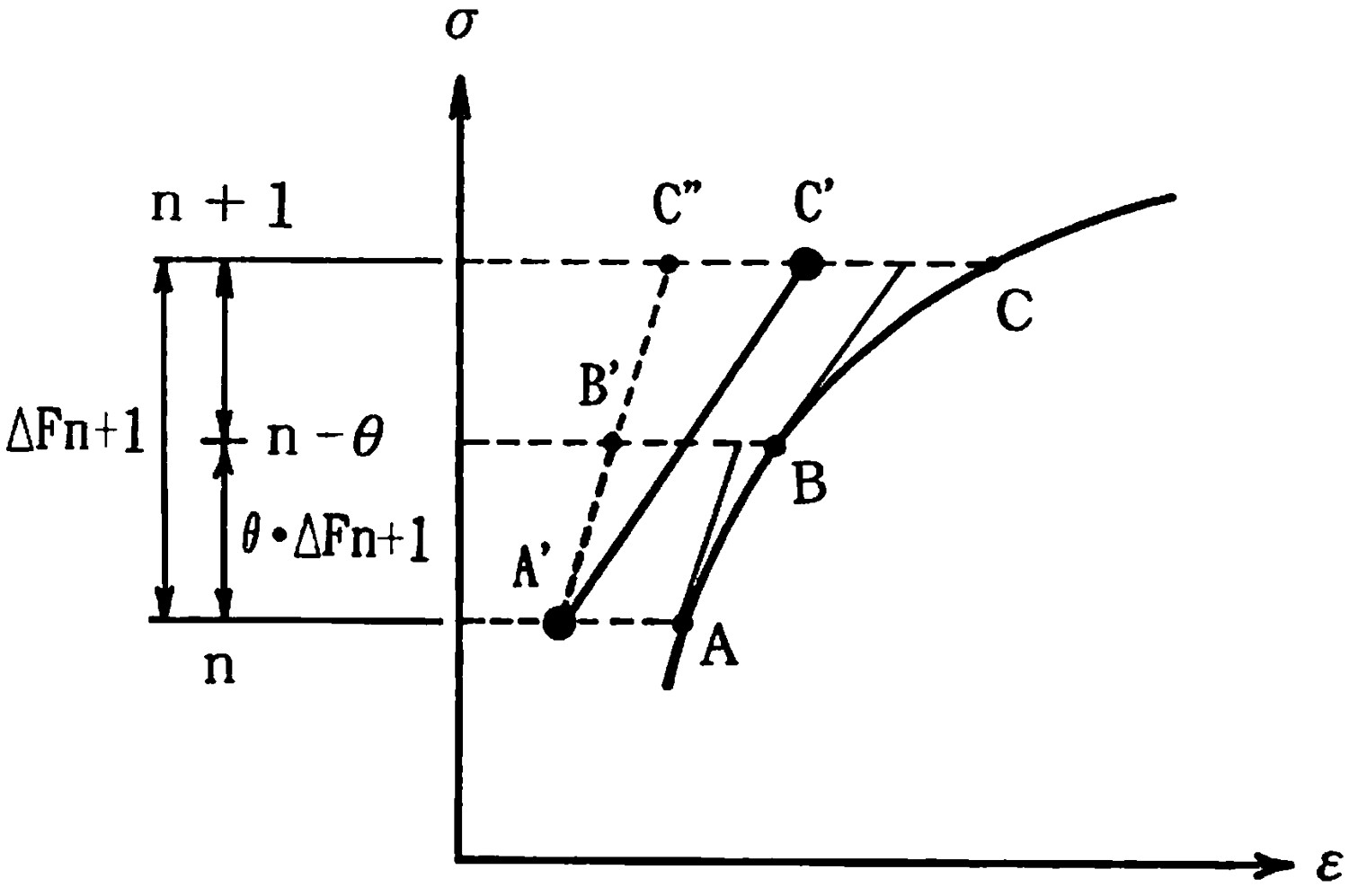
$\hspace{4em}$図3.5 Runge-Kutta法による増分法
この方法は、ある荷重増分段階で、一旦、$\theta \cdot \Delta \boldsymbol{F}^{n+1} (0 \lt \theta \lt 1)$ なる仮の増分荷重を作用させ、A点の接線剛性より B'点の応力とひずみを求める。次にこの点B'に対応するB点の接線剛性により 再度A'点から計算をやり直してC'点の応力とひずみを求める。すなわち、
\[{\rm (3.3)}
\left.
\begin{array}{lcr}
\boldsymbol{K}^{n} \cdot \Delta \boldsymbol{u}^{n+\theta}
& = & \theta \cdot \Delta \boldsymbol{F}^{n+1} \\[0.5em]
\boldsymbol{K}^{n+\theta} \cdot \Delta \boldsymbol{u}^{n+1}
& = & \Delta \boldsymbol{F}^{n+1}
\end{array}
\right\}
\]
なる関係を解くことになる。この方法は、実際の点Cからは離れているが、オイラーの方法によるC”点の値よりはC点に近づく。ただし、剛性方程式を2回解くため、1回当たりの荷重増分量に対する計算時間は増加する。
以上のように、応力とひずみの関係が連続的に変化するような場合、荷重増分法による解法では誤差が累積してゆくが、もし、
図3.1(b)のように完全弾塑性タイプであった場合は、正しい荷重増分を選択することによって誤差を累積させずに再現することができる。これは、降伏点までの区間において応力ーひずみ曲線が線形(直線)で表されるため、前回の接線勾配が、今回の応力レベルまで変化しないということに起因する。このことを拡張して考えれば、折れ線で表されるような応カーひずみ関係を持つ材料に対しても同様なことを述べることができる。
ただし、この場合、領域内の各点において応カレベルが異なるため、どの点かどの荷重レベルで降伏するかを予め想定し、荷重増分をデーターとして入力することは不可能に近い。そこで考えられたのが
山田の方法である。山田の方法では、ある要素が降伏するのに必要となる荷重増分量を応力状態から計算により決定する方法であるため、荷重増分量を入力せずにすむ。
次に、この山田の方法を用いた荷重増分法のアルゴリズムを説明する。山田の方法に関する計算アルゴリズムは以下の通りである。
- ①増分段階の始めに塑性化した(すべりの発生した)ばねとそうでないばねに分けて考え、すべり線となったばねは1章で述べた塑性化後のばね行列を用いて全体剛性行列を組み立てる。
- ②与えられた荷重増分に対して①で求めた剛性行列を解き、増分表面力 $\Delta \boldsymbol{\sigma}$ を求める。この結果得られた表面力を前回の表面力に加え合わせ、その表面力のすべてが降伏強度と等しいか、あるいは小さくなるような増分率 $r$ を求める。
- ③②で求めた $r$ を増分表面力 $\Delta \boldsymbol{\sigma}$ にかけ、前回の表面力とたし合わせることでこの段階の表面力とする。ここで、降伏強度に達したばねは以後塑性流れ則に従うものとする。
\[{\rm (3.4)}
\left.
\begin{array}{lcl}
\boldsymbol{u}^{n+1} = \boldsymbol{u}^n
+ r \cdot \Delta \boldsymbol{u}^{n+1} \\[0.5em]
\boldsymbol{\sigma}^{n+1} = \boldsymbol{\sigma}^{n}
+ r \cdot \Delta \boldsymbol{\sigma}^{n+1}
\end{array}
\right\}
\]
- ④①~③を所定の荷重になるまで繰り返す。
この記述に基づいた川井モデルにおけるプログラム化の処理手順については「離散化極限解析プログラム」に記載されているので参考にしてほしい。
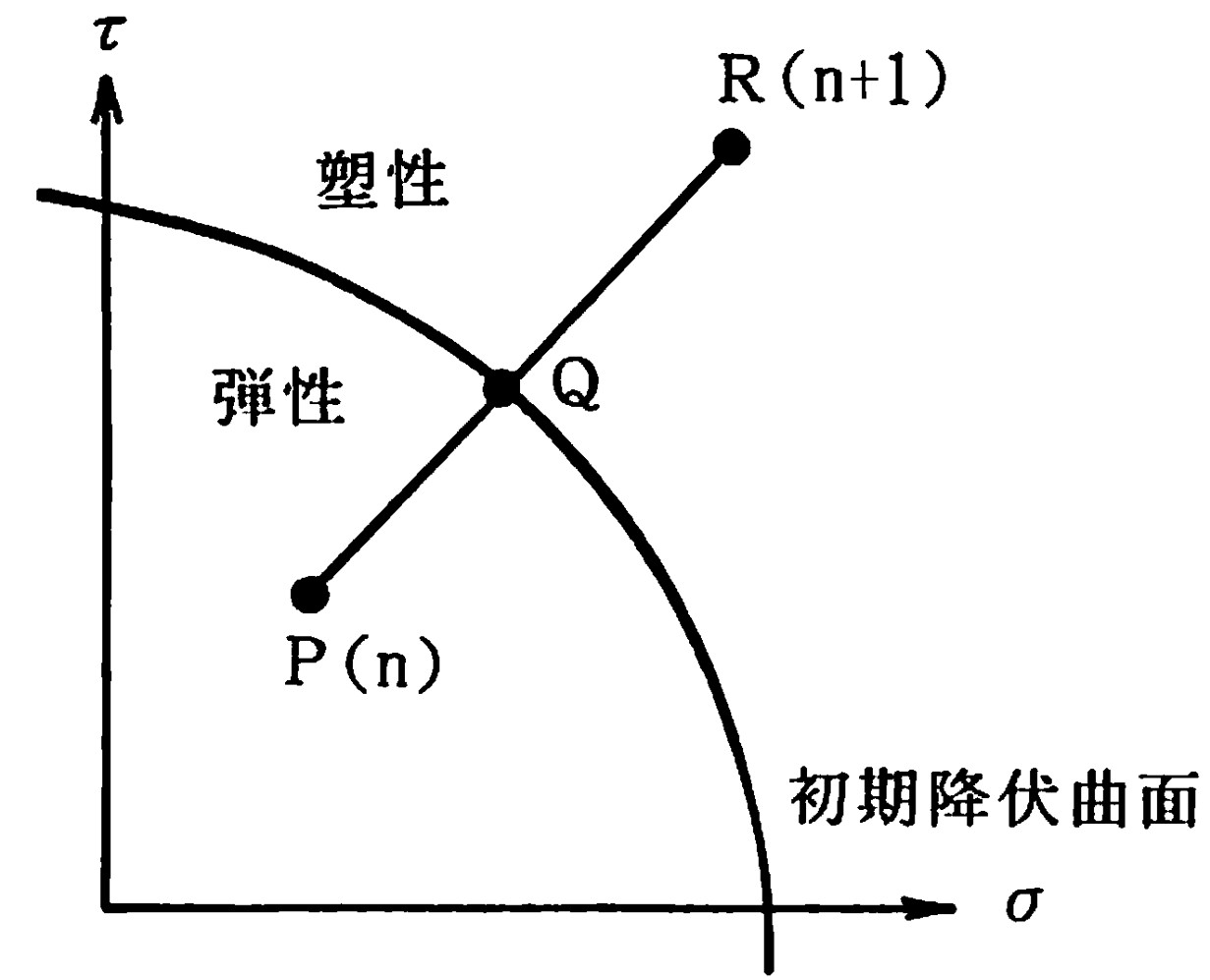
さて、山田の方法では、荷重増分量を荷重増分率という形式で求めている。
図3.6には、この荷重増分率に関する考え方が示されている。
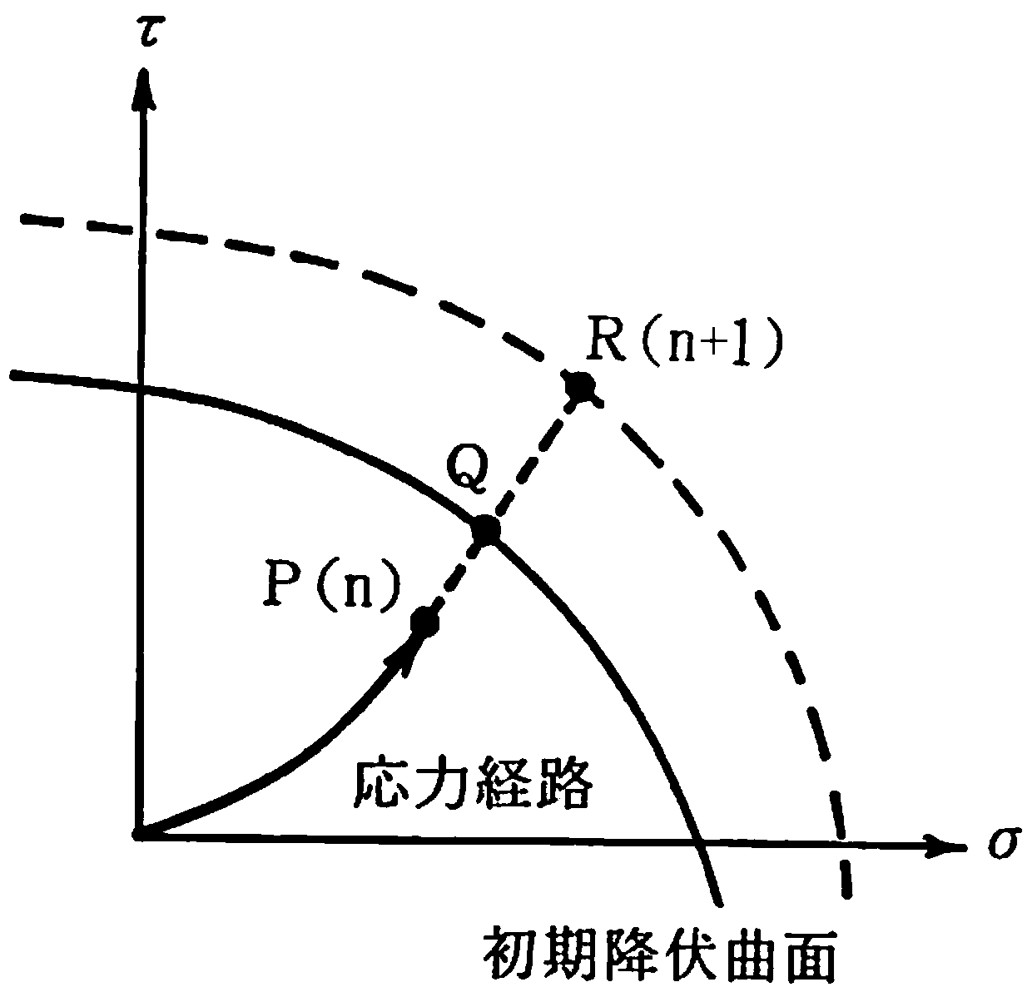
$\hspace{0em}$図3.6 山田の方法における荷重増分率
図中のP点は前回の、すなわち、nステップ目の応力状態を表しており、R点は今回求まった増分応力 $\Delta \boldsymbol{\sigma}$ を前回の値に加え合わせた仮りの(n + 1)ステップ目における応力状態を表している。P点からR点までは当然、線形的に変化していることに注意してほしい。図からも理解できるように、今回の応力増分 $\Delta \boldsymbol{\sigma}$ は $\overline{PR}$ となっている。しかし、R点で明らかに初期降伏曲面上の点を越えていれば $\overline{QR}$ という実際には起こり得ない余分な力がその点に作用していることになる。そこで、とりあえず $\Delta \boldsymbol{\sigma}$ のうち $\overline{PQ}$ で表される弾性部分を取り出す。このとき、$\overline{PQ}$ と$\overline{PR}$ の比
\[{\rm (3.5)}
r = \frac{\overline{PQ}}{\overline{PR}}
\]
を用いて、
\[{\rm (3.6)}
\boldsymbol{\sigma}^{n+1} = \boldsymbol{\sigma}^{n}
+ r \cdot \Delta \boldsymbol{\sigma}
\]
とすれば(n + 1)ステップ目の応力は降伏曲面上に載る。これは、完全弾塑性の場合、降伏応力以下では弾性状態であることを利用しており、ここまでの計算は線形計算でよいことになる。
式(3.5)で表されるような $r$ のことを山田の方法では
荷重増分率と呼んでいる。この $r$ は1つの要素(川井モデルの場合、ばねに該当する)について求めたものであるから、これをすべての要素について求め、その最小値を今回の荷重増分率とすれば、すべての要素は弾性状態か少なくとも降伏曲面上にあることになる。
このような荷重増分率より
\[{\rm (3.7)}
\Delta \boldsymbol{P}^{n+1} = r^{n+1}\boldsymbol{P}
\]
とすることで荷重増分董を決定することができる。ここで、$\boldsymbol{P}$ は初めに与えた荷重値である。最終的に荷重増分率 $r_i$ の合計が1になれば、初めに設定した荷重がすべて作用したことになる。
以上、各種の荷重増分法における解析の手順を中心に説明してきた。ここで、この荷重増分法の長所、短所を整理してみよう。
(長所)
- (1) 応カーひずみ曲線における接線勾配が非常に緩くなる強非線形問題に対しても比較的安定して解を求めることができる。
- (2) 完全弾塑性体、もしくは応カーひずみ曲線が折れ線で近似できる場合、高い精度の解を求めることができる。
- (3) 破壊の進展を追跡することができる。(応力の履歴を扱える)
(短所)
- (1) 荷重増分ステップが変わる度に剛性を変化させるため、計算時間がかかる。
- (2) 応カーひずみ関係が曲線で表される場合、誤差が累積する。
- (3) ソフトニングなどのように応カーひずみ曲線が負の勾配になる場合、扱いが単純ではない。
さて、荷重増分法そのものは非線形解析法の一つであるため、有限要素法ばかりでなく川井モデルによる離散化極限解析に対しても同様な手順により適用することができる。川井モデルによる離散化極限解析では、応カーひずみ関係を完全弾塑性タイプ、もしくは折れ線で近似し、山田の方法による荷重増分法を適用することがよく行われている。この理由は、離散化極限解析の第一の目的が、極限耐力を求めることにあるためであり、この場合、応カーひずみ関係を直線で近似しても、極限耐力に与える影響は少ないと考えられるからである。
このように考えると、荷重増分法、特に山田の方法は長所の箇所でも上げたように、より高い精度の崩壊荷重が得られるため、離散化極限解析に適した非線形解析法と考えることができる。また、荷重増分法は、すべり線の発達状況を把握することができるため、施工途中における各種の対策工法の検討にも利用できるものと思われる。
山田の方法においてボイントとなるのが荷重増分率の計算方法であった。川井モデルではベクトル量としての表面力を扱うため、主応力を扱う有限要素法とは若干異なる。ここでは、破壊条件としてモール・クーロンの条件を用いた場合の荷重増分率の計算方法について説明する。
図3.7はモール・クーロンの条件を用いた場合の応力経路を示したものである。
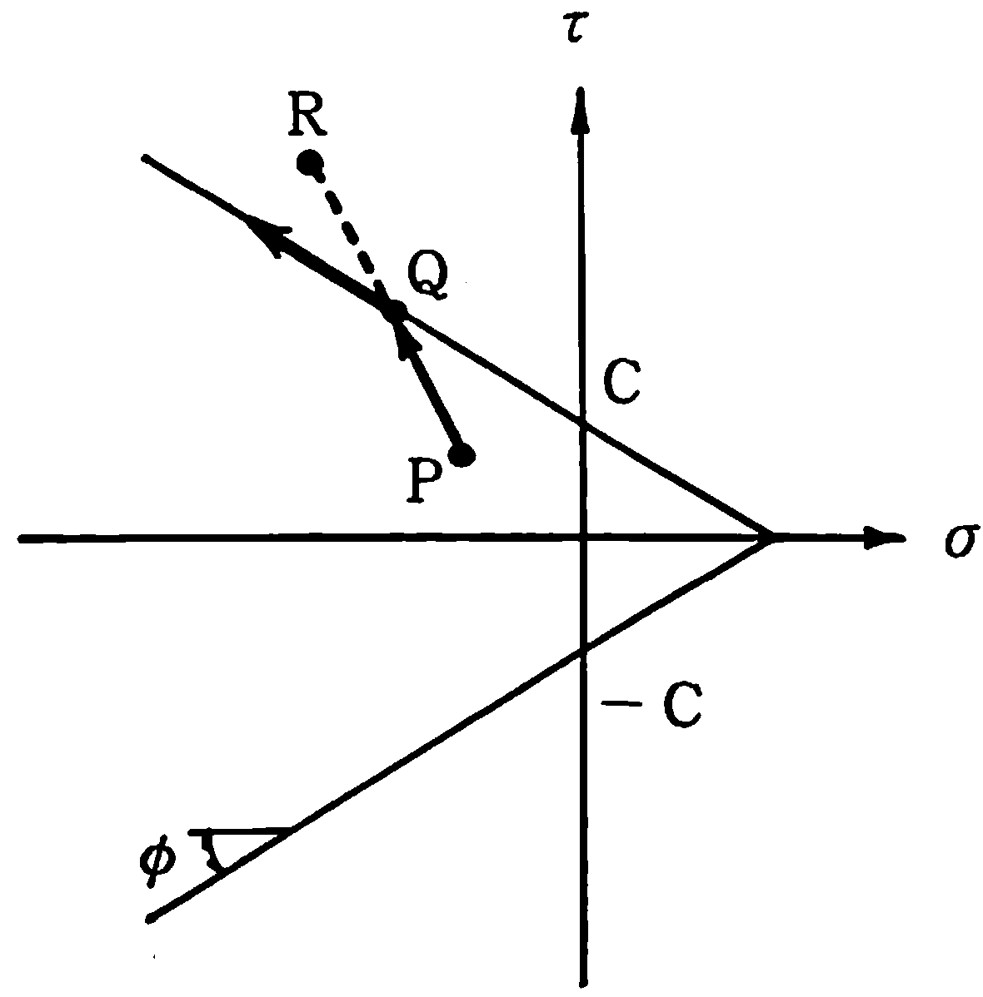
$\hspace{0em}$図3.7 モール・クーロンの条件における応力経路
いま、前回までの表面力を $(\sigma_n,\tau)$ とし、新しい荷重増分による増分表面力を $(\Delta \sigma_n,\Delta \tau)$ とすれば、今回の表面力は
\[{\rm (3.8)}
( \tau + r \cdot \Delta \tau)^{2} \leq
\{ c - (\sigma_{n} + r \cdot \Delta \sigma_{n}) \tan \phi \}^{2}
\]
なる関係を満足していなければならない。ここで、$r$ は該等するばねにおける未知の荷重増分率である。
式(3.8)を $r$ について整理すると、
\[{\rm (3.9)}
A \cdot r^{2} + B \cdot r + C \leq 0
\]
\[\hspace{6em}
\begin{array}{l}
A = \Delta \tau^{2} - (\Delta \sigma_{n} \tan \phi)^{2} \\[0.5em]
B = 2 \{ \tau \Delta \tau - ( c - \sigma_{n} \tan \phi )
\Delta \sigma_{n} \cdot \tan \phi \} \\[0.5em]
C = \tau^{2} - (c - \sigma_{n} \tan \phi)^{2}
\end{array}
\]
となる。ここで、等号が成立するのは、今回の表面力がちょうど降伏曲面上の点 $Q$ に載った場合である。山田の方法では、この等号が成立するための荷重増分率 $r$ を、すでに降伏しているばねを除き、すべてのばねについて求める。このようにして得られた値のうち、最小の値を系全体の荷重増分率とすれば、表面力は弾性状態か少なくとも降伏曲面上にあることになる。一旦、 降伏したばねについてはは、
図3.7に示すよう降伏曲面上を移動するものとし、ばね剛性行列を
1章で説明した塑性化後の剛性行列に変更する。
他の破壊条件を利用する場合においても、ここで説明したように、合力によって表された式を利用すれば、川井モデルによる離散化極限解析においても、従来の有限要素法で利用されているような荷重増分法を適用することができる。
地盤の応力解析における問題点の一つに現地盤の初期応力の推定がある。例えば、切土やトンネル安定問題などの掘削が伴う解析、あるいは盛土などのように既存の斜面に新たに荷重が加わるような解析、支持力解析など、どの問題を取り上げても初期応力の状態が解析結果に影響を与えていることがわかる。
解析を行うに当たり、このような初期応力を計測などによって得られた結果から推定し、入力という手段で取り込むことも考えられるが、一般的には広範囲な領域で、且つ不均質な地盤を扱うことが多いため、自重を荷重として計算により求めることがよく行われている。
計算により初期応力状態を求める場合、破壊がどのように進展してゆくかということよりも、むしろ、最終的な応力状態がどのようになるかが重要である場合が多い。これは地盤の応力解析が多くの場合、初期応力状態を基礎としてその後の施工による地盤の変化に重点を置いているためである。前節において説明した荷重増分法は、破壊の進展状況や崩壊荷重を求めるといった強非線形問題に適した解析法であり、初期応力の分布状態を知るといった弱非線形問題(自重により崩壊現象が発生しないという意味で)の場合には必ずしも適切な解法とはいいきれない。特に、応カーひずみ関係が前節の
図3.1(c)で示したように曲線で表される場合は増分荷重の選び方により初期応力状態に誤差が含まれるため、注意が必要である。
そこで、本節では荷重レベルに応じた破壊の進展状況は把握することができないが、応力状態をより簡単に求めることのできる反復法について説明する。反復法は計算によって得られた解を修正してゆく方法で、これに含まれる代表的な非線形解析法として以下の三つが上げられる。
- 1) 直接反復法(割線係数法)
- 2) Newton-Raphson法
- 3) 修正Newton- Raphson法
三つの方法のうち、初めの二つは収束計算過程において、順次、剛性を変化させてゆく方法であり、三番目は初めに設定した剛性を最後まで利用する方法である。応カーひずみ関係が図3.1(c)で示したように曲線で表されることを前提としてこれらの方法を説明しよう。
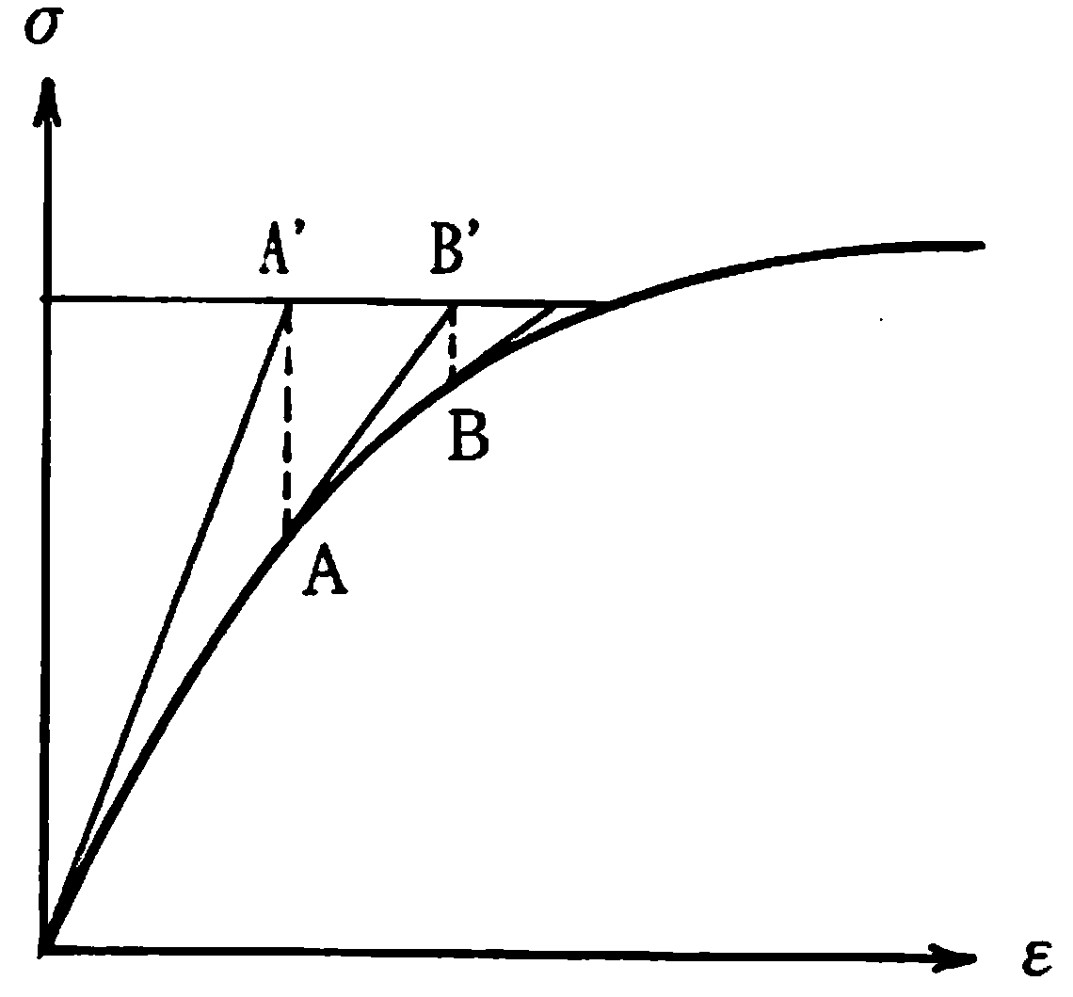
図3.8は直接反復法の計算過程を示した簡略図である。この方法では全荷重を作用させ、接線剛性(必ずしも接線剛性である必要はない)をもとに、$A'$ 点の応力とひずみを求める。しかし、このような応力状態は実際の状態と異なるため、$A'$ 点のひずみに対応する応カーひずみ曲線上の点 $A$ を求め、原点 $0$ と $A$ 点を結ぶ割線剛性を用いて再度計算をやり直す。この結果 $B'$ 点の値が求められるが、もし、$B'$ 点の値が実際の値と大きく異なるようであれば、初めの手順と同様、$B$ 点を求め $\overline{OB}$ の割線剛性を用いて再計算する。これを満足する結果が得られるまで繰り返す。
$\hspace{4em}$図3.8 直接反復法
このように、直接反復法では割線剛性を用いることから、割線係数法とも呼ばれている。反復法では、弱非線形問題、すなわち、応カーひずみ曲線が勾配の急な直線に近いほど収束計算回数が少なくて済むことが容易に理解できよう。もちろん、収束判定条件の考え方によって収束計算回数は変動する。一般的にこの収束判定条件として、解のノルムを取る方法が利用されている。
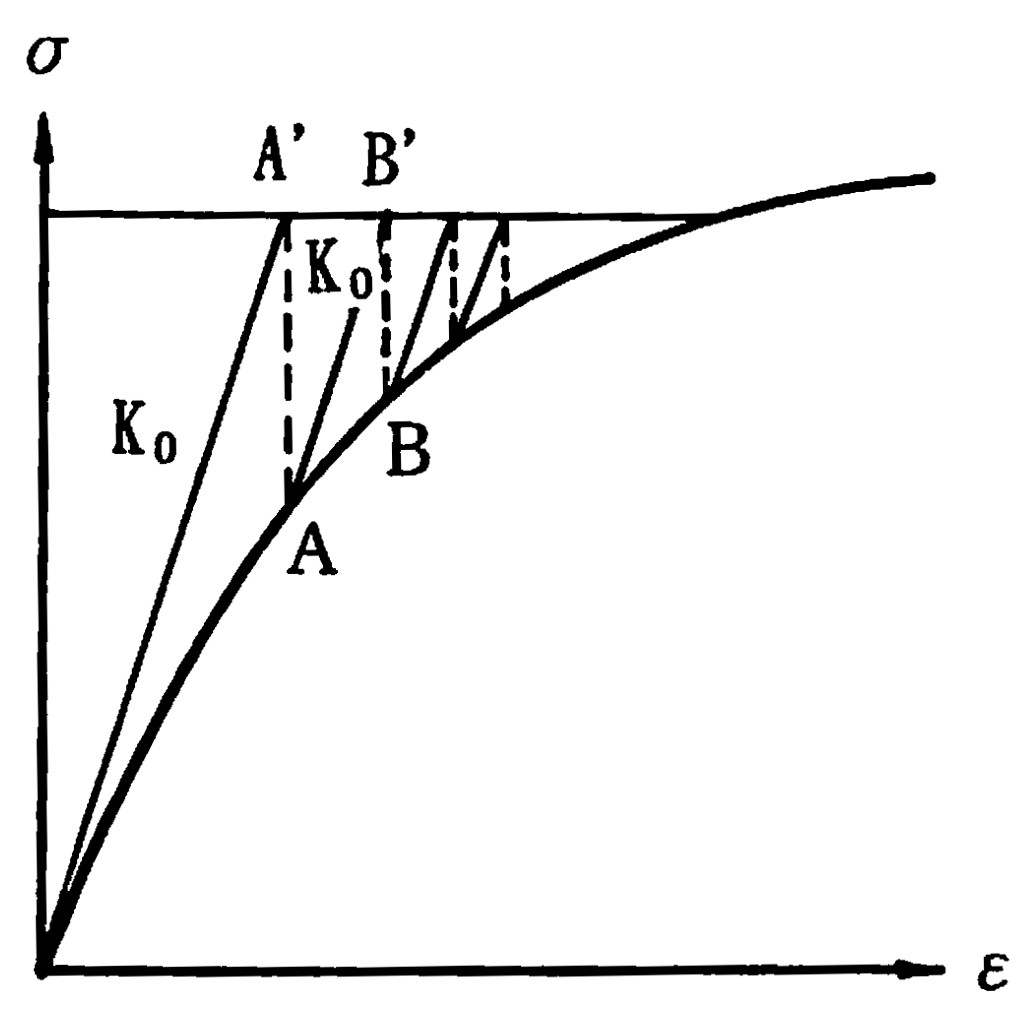
(2)のNewton-Raphson法は応カーひずみ曲線における接線剛性を利用して解を修正する方法である。荷重増分法における接線係数法が荷重増分量の調整により誤差の累積を防ごうとしているのに対し、この方法では同じ接線剛性を利用することには変わりないが、図3.9に示すよう、余剰力の再配分により防いでいる。図に沿ってこのことを説明しよう。まず、全荷重を一旦作用さ せ、$A'$ 点を求める。このとき、本来の点は $A$ であるため、$\overline{AA'}$ なる矛盾が生ずる。そこで、$A$ 点に戻り、この点を原点とし、且つこの点の接線剛性を用いて再度計算し$B'$ 点を求める。このときの荷重は全荷重ではなく再配分される $\overline{AA'}$ である。この計算過程を解が収束するまで繰り返す。この方法では接線剛性を用いているため、弱非線形問題の場合、収束性が良いが、収束計算の度に剛性を変えなければならず、荷重増分法同様、計算アルゴリズムが若干複雑となる。
$\hspace{1em}$図3.9 Newton-Raphson法
一方、(3)の修正Newton-Raphson法では、このような欠点を補うため、収束過程において、図3.10に示すような初期接線剛性をそのまま利用している。この場合、弾性解析用のプログラムを若干変更するだけで済み、計算時間の短縮化が期待できる。ただし、図からも理解できるように、非線形性が強くなった場合、解が安定して得られるものの、収束するまでの計算回数も増加する傾向にある。
$\hspace{0em}$図3.10 修正Newton Raphson法
以上の関係を剛性方程式により示してみよう。(1)の反復法では
\[{\rm (3.10)}
\boldsymbol{K}^{n} \cdot \boldsymbol{u}^{n+1} = \boldsymbol{P}
\]
なる剛性方程式を解いていることになる。ここで、$\boldsymbol{K}^n$ はn回目の計算より求まった値から作成された割線剛性による剛性行列である。一方、 (2)のNewton-Raphson法の場合は、
\[{\rm (3.11)}
\boldsymbol{K}^{n} \cdot \Delta \boldsymbol{u}^{n+1} = \boldsymbol{F}^{n}
\]
を解いていることになる。ここで、$\boldsymbol{K}^n$ は前回の応力状態における接線剛性を用いて作成された剛性行列であり、$\boldsymbol{F}^n$ は $n=0$ の場合全荷重 $\boldsymbol{P}$ を、それ以外は $\overline{AA'}$ に示されるような余剰力による再配分される力を示す。最終的な解は式(3.1)のような重ね合わせによって求める。(3)の修正Newton- Raphson法は
\[{\rm (3.12)}
\boldsymbol{K}^{0} \cdot \Delta \boldsymbol{u}^{n+1} = \boldsymbol{F}^{n}
\]
のように、式(3.11)において剛性方程式が初期剛性を用いている以外、先のNewton-Raphson法と同じである。
以上から理解できるように、(1)の直接反復法では、方程式を新たに解き直しており、(2)のNewton-Raphson法と(3)の修正Newton-Raphson法は余剰力から計算される力を新たな外力として重ね合わせにより解を求めている。後者の場合、余剰力から計算される外力の求め方が問題となる。初期応力法や初期ひずみ法は(3)の修正Newton-Raphson法と同様、初期剛性を利用する方法で、この外力の求め方、すなわち、応力の修正方法に特徴がある。
次ぎに応カーひずみ関係が完全弾塑性タイプの場合について考えてみよう。一般に反復法では収束性をよくするため、応カーひずみ関係に若干のハードニングを導入することが行われている。しかし、このような処理を行ったとしても直接反復法やNewton-Raphson法のように剛性を修正する方法では計算アルゴリズムも複雑なものとなり、収束も悪いため荷重増分法と比較してメリットが少ない。特に、直接反復法では収束計算回数が増えるため、計算時間の点から考えてみても増分法における山田の方法より不利になることも多い。また、完全弾塑性の場合、荷重増分法では山田の方法により正確な崩壊荷重が得られるのに対し、反復法では全荷重を一度に作用させるため、崩壊荷重を求めるのが難しい。このように、反復法は完全弾塑性の場合、一般的な応カーひずみ関係より計算上のメリットが減少する傾向にある。
ここで、反復法の長所と短所を簡単に整理しておこう。
(長所)
- (1) 弱非線形問題の場合、累積誤差を避けることができ、最終応力状態が容易に求まる。
- (2) 修正Newton- Raphson法の場合、アルゴリズムが簡単でプログラミングが容易である。このことは、計算時間の短縮化にもつながる。
- (3) ソフトニングなどの現象が容易に取り込める。
(短所)
- (1) 応力の履歴を扱うことができない。
- (2) 強非線形問題の場合、収束性が悪くなる。特に、応カーひずみ関係が完全弾塑性 の場合は顕著となる。
- (3) 剛性を変える方法は計算時間の短縮化などの点において利点が減少する場合もある。
以上のような短所は荷重増分法との組み合わせにより改善することが可能で、このような方法のことを混合法と呼ぶこともある。次に、川井モデルによる離散化極限解析にこの混合法を適用する方法について説明しよう。
まず始めに荷重増分法と同様、与えられた荷重を小さな増分荷重に分割する。次ぎに、分割された個々の増分荷重に対し、以下のような反復法による収束計算を行う。
- ①荷重の増分を与え、対応する増分応力(弾性応力として)と増分ひずみを計算する。
- ②①において降伏条件を越えているばねがあれば弾性部分の応力(ひずみ)と余分な応力(ひずみ)に分割する。
- ③②において分割された残りのひずみは実際には塑性ひずみとして働くはずであるため、塑性化後の構成式 $\boldsymbol{D}^{p}$を利用して塑性化後の応力を求める。
- ④③で求めた塑性化後の応力と②において求められた余分な応力の差を残差として次ぎの収束計算の荷重とする。また、弾性部分の応力と塑性化後の応力の和が収束過程における今回の応力となる。
- ⑤②~④を収束するまで繰り返す。
図3.11は上記の収束過程を図化したものである。この方法で問題となる点の一つはいかにして弾性部分の応力(ひずみ)と余分な応力(ひずみ)に分けるかということである。
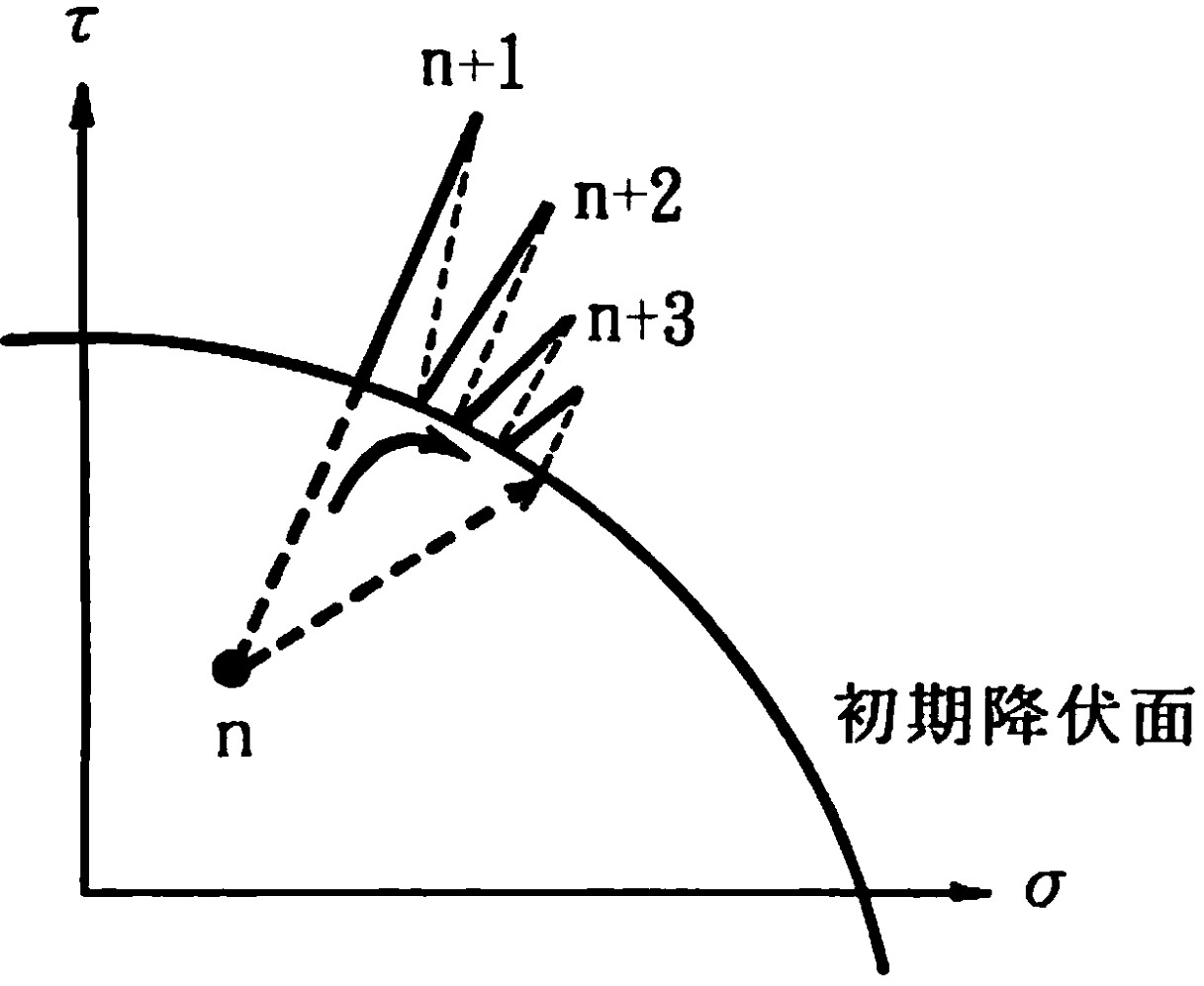
$\hspace{1em}$図3.11 反復法の収束計算
図3.12は収束過程の第1回目の図である。もともとP点にあった応力値が増分荷重の作用により$R$点に飛び出した状態を示している。余分な応力と弾性応力を分離するためには $Q$ 点を知り、$\overline{PQ}$ と $\overline{PR}$ の比を求めればよい。
$\hspace{4em}$図3.12 余剰力
すなわち、
\[{\rm (3.13)}
\Delta \boldsymbol{\sigma}_{n+1}^{(e)} =
\Delta \overline{\boldsymbol{\sigma}}_{n+1}
\frac{\overline{PQ}}{\overline{PR}}
\]
なる計算を行えばよい。式(3.13)における係数 $\overline{PQ}/\overline{PR}$ は荷重増分法における山田の方法の荷重増分率 $r$ と一致する。したがって、はじめて降伏を経験するばねについては山田の方法における荷重増分率を計算し、それを利用して弾性部分の応力(ひずみ)と余分な応力(ひずみ)に分割すればよい。一度、降伏条件を破り、再配分を経験したばねについてはひずみ増分の方向、すなわち、勾配が負にならない限り上記の③と④を繰り返す。このことは、2回目以降、荷重増分率の計算が不要であることを意味している。なお、収束判定条件としては解のノルムをとる従来の反復法の判定条件を利用してもかまわないし、また、このアルゴリズムの場合は残差力を用いても可能である。
以上のような混合法を用いて弾塑性解析を行っても、荷重増分が大きすぎたりすると収束性は改善されないこともある。その場合、ある荷重増分における収束計算が終了した後、塑性化後の剛性行列を利用することによって収束性を改善することができる。しかし、崩壊荷重を求めるといった点では荷重増分量の決定に十分注意を払わなければ依然として山田の方法と比較しメリットが生じないこともある。
さて、簡単な数値計算により荷重増分法における山田の方法による解とここで説明した混合法による解を比較してみよう。図3.13はポンチの押し込み問題に対する要素分割と材料定数が示されている。
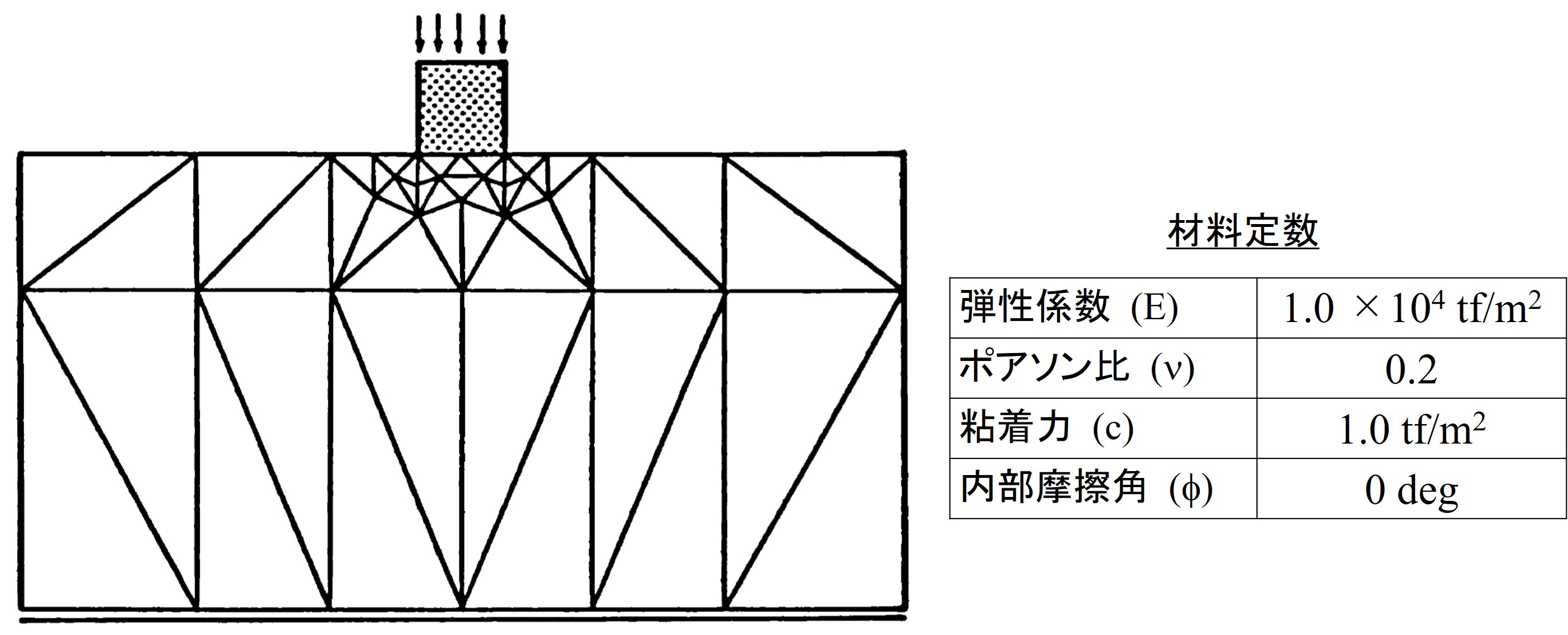
$\hspace{6em}$図3.13 ポンチの押し込み問題
図3.14には山田の方法によるすべり線状態が示されている。山田の方法による崩壊荷重 $(P/2C)$ は2.66であった。解析解が2.57であることを考えると非常に高い精度で崩壊荷重が求まっていることがわかる。
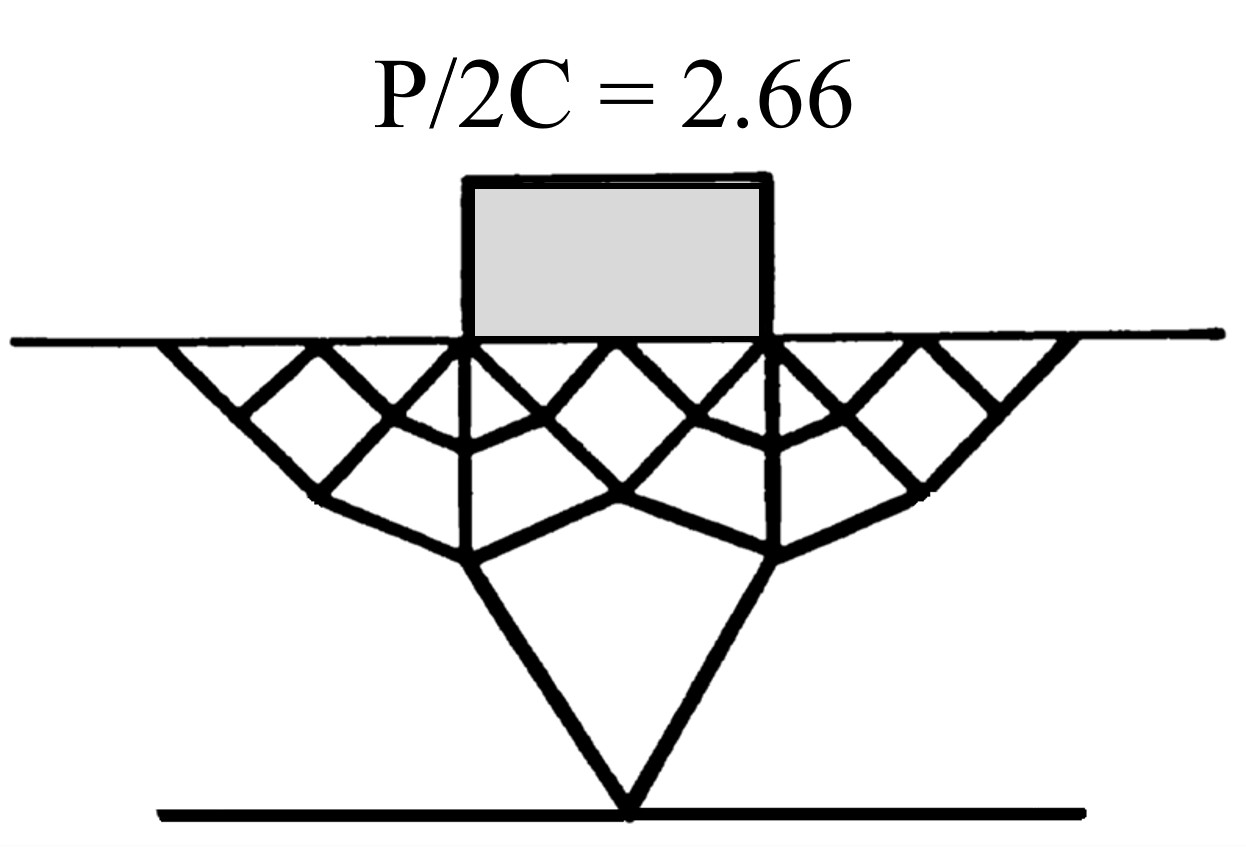
$\hspace{2em}$図3.14 荷重増分法によるすべり線
一方、図3.15は混合法によって求めたすべり線が画かれている。図(a)が荷重増分量 $P/2C$ を(1.325.0.65.0.65)とした場合で、図(b)は(1.325.0.65.0.325.0.325.0.025)とした場合である。なお、各荷重増分段階における収束計算終了後の剛性行列には塑性化後のものを利用している。図からも理解できるように、混合法では最終荷重段階でのすべり線がメカニズムを形成していない。
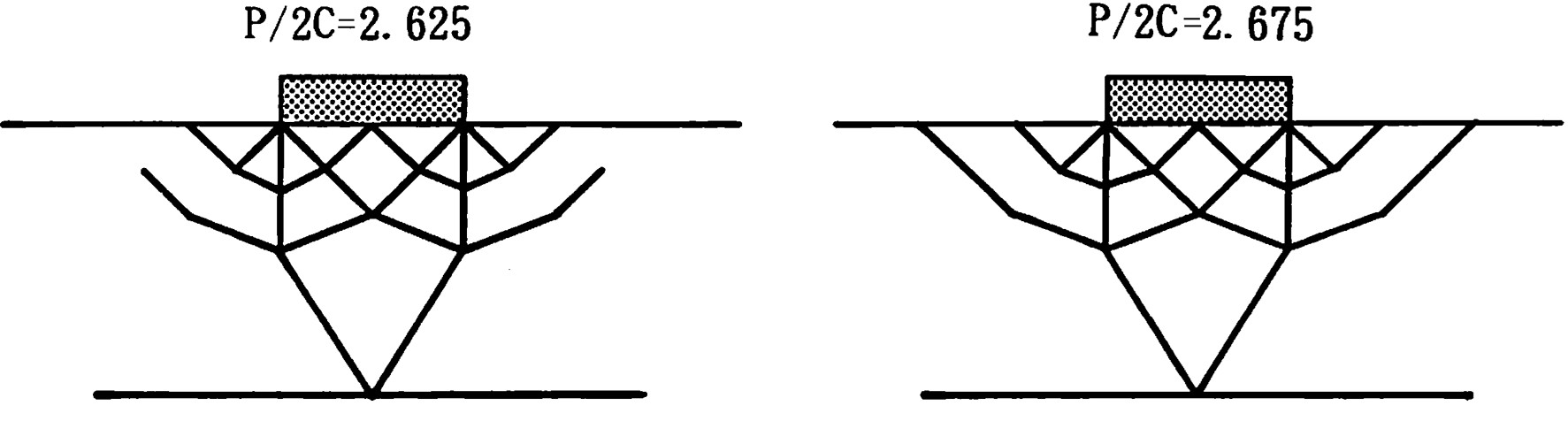
$\hspace{5em}$(a)3分割 $\hspace{9em}$(b)5分割
$\hspace{7em}$図3.15 反復法によるすべり線
図3.16は荷重ー変位曲線を比較したものである。荷重増分法と反復法とでは多少異なっているが増分荷重量を細分すれば徐々に近づくものと思われる。
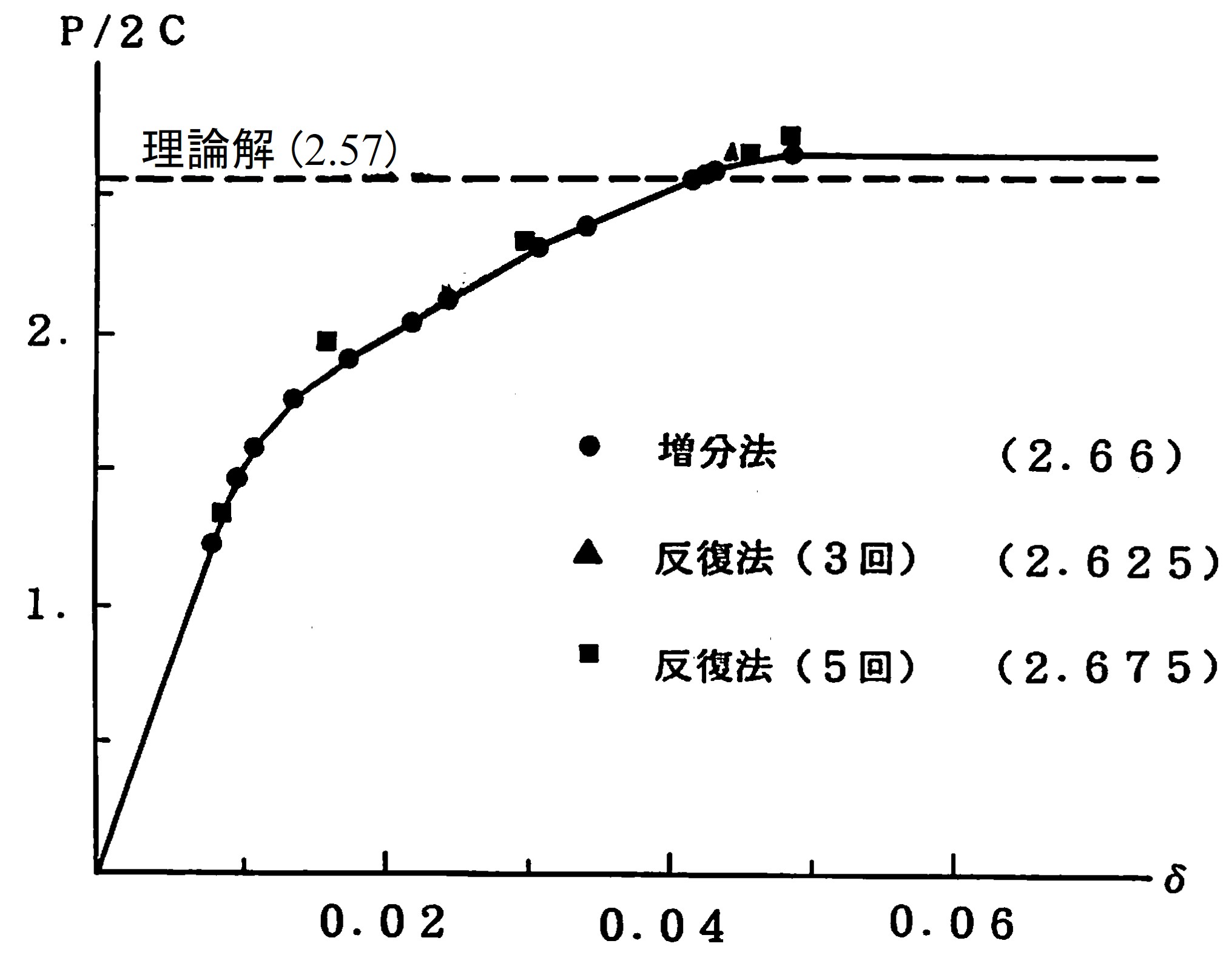
$\hspace{6em}$図3.16 荷重-変位曲線
平面問題に関する崩壊荷重を解析的に求める場合、すべり破壊を要因とする極限解析が一般的に利用されている。また、モール・クーロンの条件などの破壊条件を利用する場合は引張応力も問題となるが、この場合は引張クラックの発生に伴って生ずる解放力をそのまま保持して極限荷重を求めているものが多い。
しかし、地盤内に設置された基礎構造物などのように、異なった材料が混在するような場合や構造物における部材の接合部では、いわゆる、付いた離れたといった接触現象が生ずる。また、地盤などのように比較的引っ張りに弱い材料では接触領域以外の箇所においても引張破壊が広がることも多い。このような現象は実際の地盤においてもよく見られることであり、数値解析を実施する上で考慮すべき現象である。もし、これらの現象を取り入れなかったり、引っ張り強度を保持する極限解析により崩壊荷重を求めた場合、上界定理を基礎としていれば危険側の値を与えるおそれがある。
したがって、引っ張り破壊や接触現象を伴うような問題に対して、上下界定理を基礎とする極限解析を適用する場合、予めそのような現象が発生する箇所を設定しておく必要がある。しかし、現実には接触領域がどの程度の大きさなのか、また、引っ張り破壊領域がどの程度広がるのか理解できないことの方が多く、各種破壊パターンが混在するような問題の場合、何等かの数値計算手法に頼らざるを得ないのが現状である。
2章で説明したTension-Crack法はすべりを無視し、単純に接触現象や引っ張り破壊を取り扱うための非線形解析法である。また、3.3節で説明した荷重増分法は応力解放の伴う接触現象や引っ張り破壊を単純に扱うことかできない。これは、引っ張りクラックなどが一旦発生すると、引き続きその解放力によって別の箇所に引っ張りクラックが発生し、厳密に崩壊荷重を求めようと思えばこれら解放力に対しても荷重増分法を適用せざるを得なくなり、脆性材料では収束性が極端に悪くなる恐れがあるためである。本節では、このような接触や引っ張り破壊の伴う問題に対する非線形解析法について説明する。ただし、すべりに関して応カーひずみ関係は完全弾塑性もしくは折れ線で近似できるものとする。
破壊条件として、図3.17に示す引張破壊を考慮したクーロンの条件を考える。
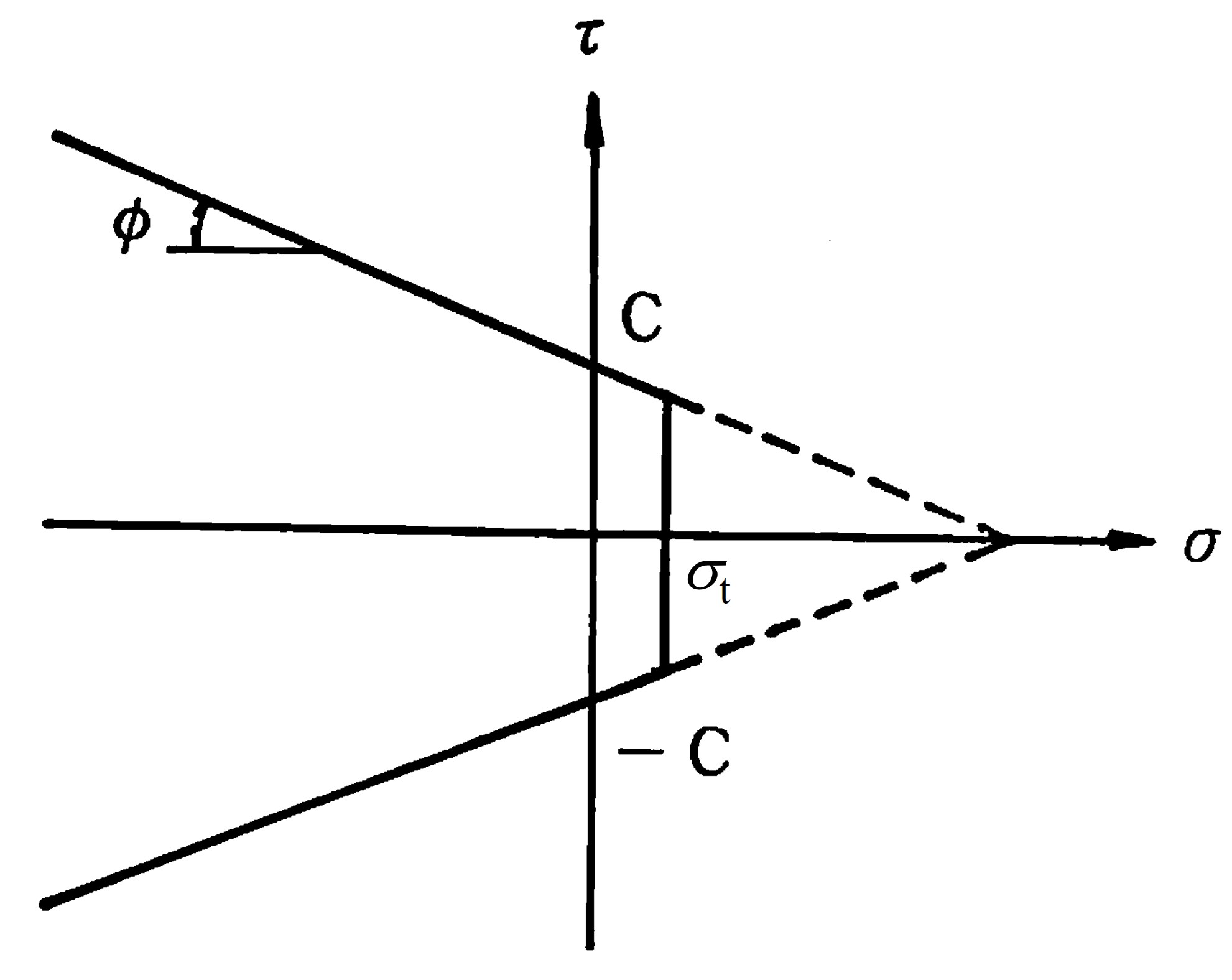
$\hspace{0em}$図3.17 引張破壊を考慮したクーロンの条件
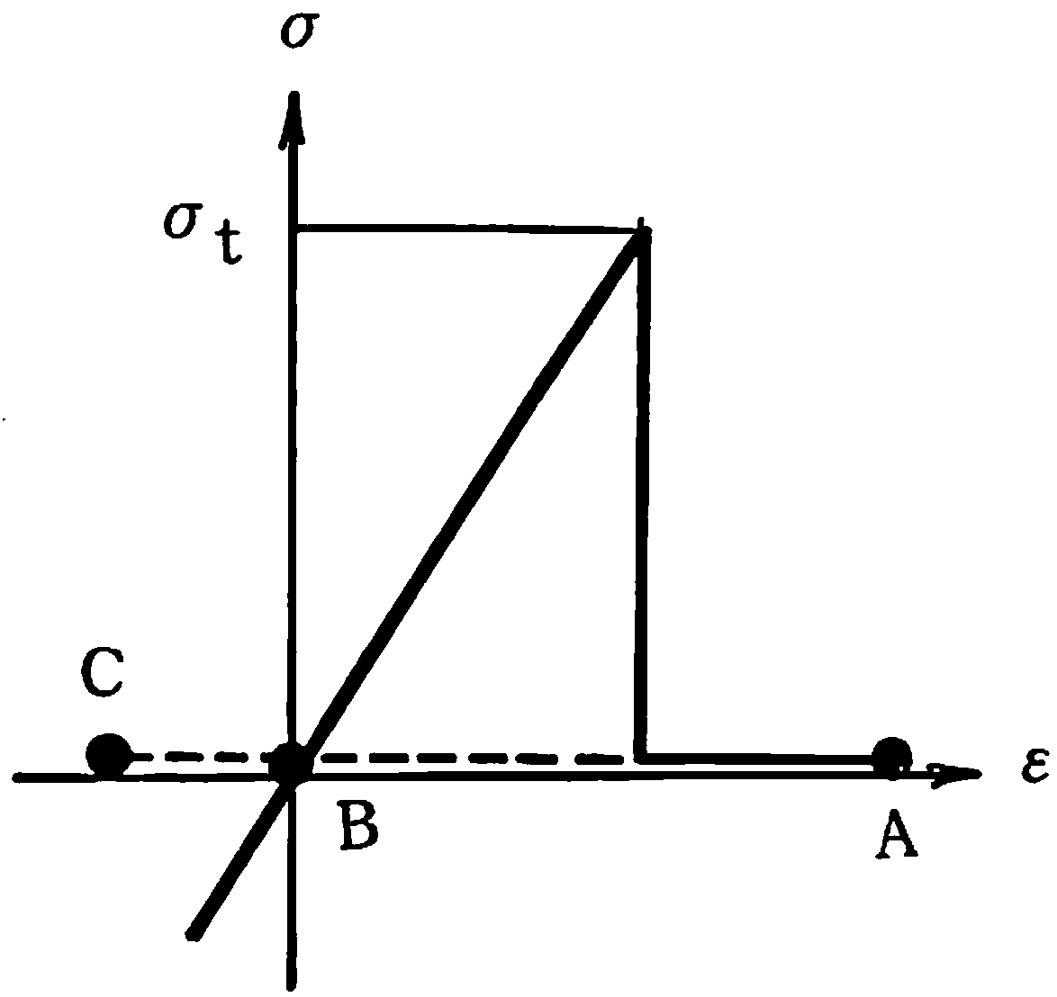
もし、応力が弾性状態から、あるいはすべり状態から降伏曲面上を移動して引張強度 $\sigma_t$ に達した場合、応カーひずみ関係は図3.18に示すよう応力低下が生ずるものとする。
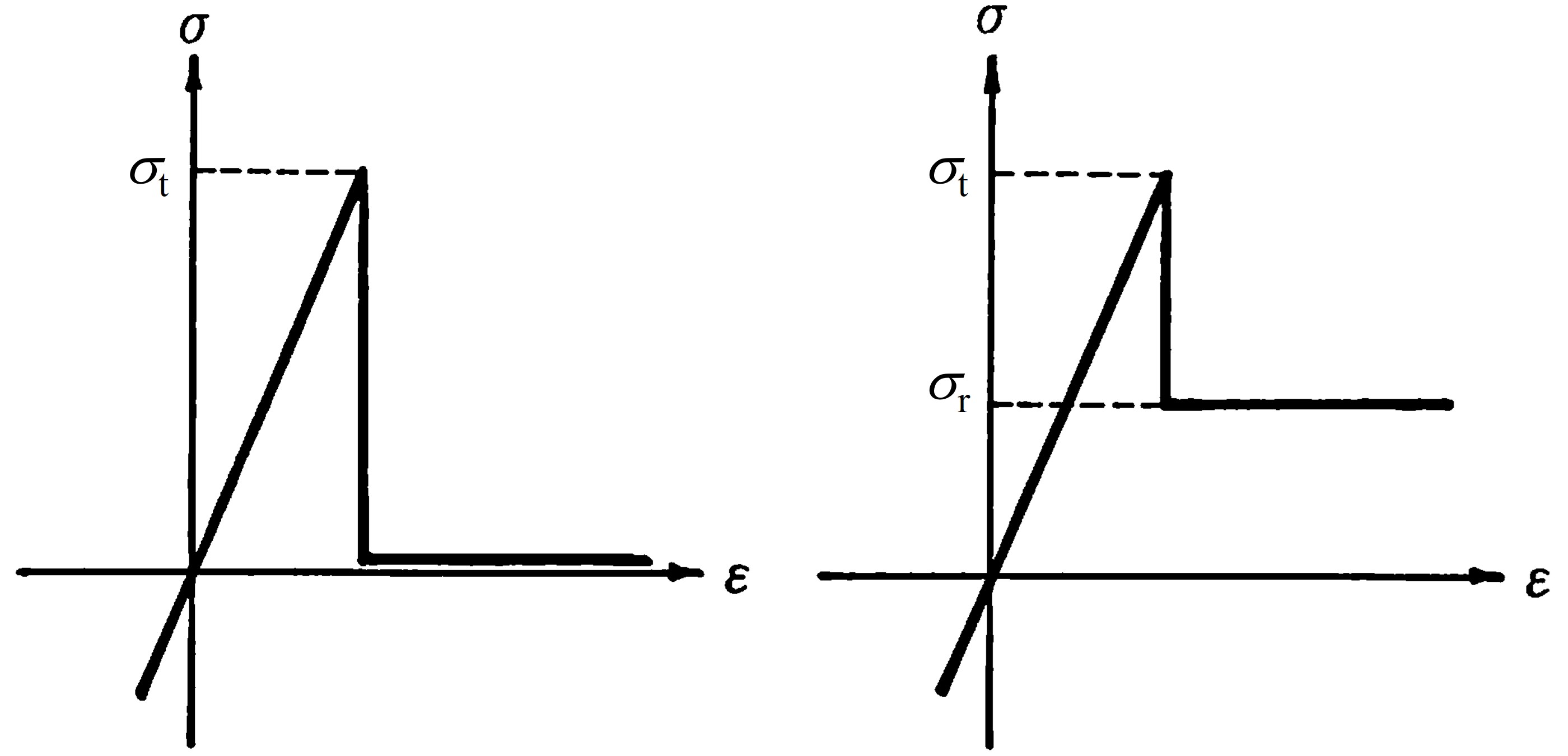
$\hspace{2em}$(a)接触型 $\hspace{6em}$(b)引っ張り破壊型
$\hspace{3em}$図3.18 引張破壊時の応力-ひずみ関係
図(a)は接触型の応カーひずみ関係で、引っ張りクラック発生後、残留応力が0となっている。一方、図(b)は引っ張り破壊型で、残留応力は $\sigma_r$ とする。もし、$\sigma_r=0$ であるなら接触型と同一になり、$\sigma_r=\sigma_t$ の場合は引っ張り破壊により解放力は発生しない。解放される応力の計算は2.4節において説明したように、図3.18(a)の場合、
\[{\rm (3.14)}
\boldsymbol{F} = - \int_{l_{35}} \boldsymbol{} \boldsymbol{\sigma} ds
\]
として求められる。ここで、$\boldsymbol{\sigma}=(\sigma_t, \tau)$ であり、引っ張りクラック発生時のせん断応力についてもすべて解放する必要がある。一方、図3.18(b)の場合、垂直応力については $\boldsymbol{\sigma}=\boldsymbol{\sigma}_r-\boldsymbol{\sigma}_t$ を解放すればよいが、せん断応力については垂直応力の解放率と同一にするとか、すべての値を解放するといったように、問題に応じて解放する量を選択する必要がある。また、クラック発生後の剛性についても、前者の場合は垂直、せん断の両者の剛性を0とすればよいが、後者の場合は垂直方向の剛性のみ0とし、せん断についてはある程度の剛性を残すことも問題によっては必要である。
以上の準備のもと、荷重増分法における山田の方法を応用した非線形解析法のアルゴリズムについて説明する。この方法は、全作用荷重を適切な増分荷重に分割し、各荷重増分段階で残りの荷重量をカウントしながら荷重増分法を適用する方法であり、もし、引っ張りクラックなどの発生により解放力が生じた場合、それを残りの荷重量に加えることで近似的に引っ張りクラックや接触現象を取り込むことができる。
本解析法は、上述のように、基本的には各荷重増分段階において荷重増分法を適用するため、すべりに対してばかりでなく、引っ張り破壊や接触が発生するのに要する荷重増分率を計算する必要がある。
せん断破壊に対する荷重増分率は従来の山田の方法と同様、図3.19のようにして決定することかできる。一旦すべり破壊が生じたばねは通常の塑性流れ則に従い、破壊曲面上を移動するものと考える。もちろん、除荷や負荷などの現象も従来通り考慮する。
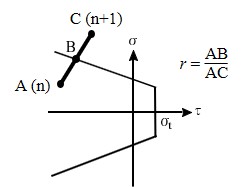
$\hspace{0em}$図3.19 せん断破壊時の荷重増分率
一方、引っ張り破壊に対する荷重増分率は、図3.20のような応力状態を考え、
\[{\rm (3.15)}
( \sigma + r \cdot \Delta \sigma ) = \sigma_{t}
\]
により決定する。ここで、$\sigma$ は前回までの垂直応力であり、$\Delta \sigma$ は今回の仮りの増分垂直応力を示している。引っ張りクラックによる応力解放はこのような荷重増分率を求め、一旦応力値を引っ張り強度まで下げた後、次ぎのステップにおいて行われる。
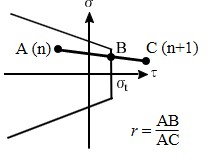
$\hspace{0em}$図3.20 引っ張り破壊時の荷重増分率
もし、$C$ 点が、図3.21のように、混合領域に入った場合は破壊パターンとしてせん断と引っ張りの両者が考えられる。図中、$C$ がせん断破壊の場合で $C'$ 点が引っ張り破壊の場合である。このような場合は両者の荷重増分率を計算し小さい方の値を採用すれば、複雑な判定条件を用いずとも荷重増分率を計算することができる。
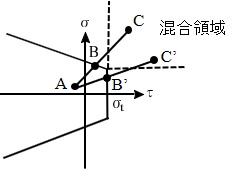
$\hspace{0em}$図3.21 混合域における荷重増分率
引っ張り破壊が生じたばねについては、川井モデル独特の物理量である2要素間の相対変位を利用して再接触に関する増分率を計算しておく必要がある。図3.22は接触型の場合の荷重増分率の計算方法を示したものである。
$\hspace{2em}$図3.22 接触時の荷重増分率
引っ張りクラックが発生し、クラックが開いている間は、垂直方向の相対変位は正の方向に移動する。しかし、もし別の箇所の引っ張り破壊などによって相対変位が反対の方向に移動し、負の値になると2要素は再び接触したことになる。そこで、図3.22のように
\[{\rm (3.16)}
r = \frac{|\varepsilon^{n}|}{| \Delta \varepsilon^{n+1}|}
\]
によって再接触に必要な荷重増分率を計算する。
以上のようにして全ばねに対する荷重増分率を各破壊パターン毎に計算し、そのうちの最小の荷重増分率を今回の荷重増分率として採用する。この最小荷重増分率を与えたばねの破壊状態が引っ張り破壊なら、先に示したように応力解放を次ぎのステップで行う。
解放力が発生しない場合の残りの荷重量は現在の荷重 $\boldsymbol{P}^n$ に対し、荷重増分率を $r_n$ とすれば、次ぎのステップで用いる残りの荷重量 $\boldsymbol{P}^{n+1}$ は
\[{\rm (3.17)}
\boldsymbol{P}^{n+1} = (1-r_{n})\boldsymbol{P}^{n}
\]
となる。したがって、$n$ ステップ目の残りの荷重量は初めに与えた荷重を $\boldsymbol{P}$ として以下のように求めることができる。
\[{\rm (3.18)}
\boldsymbol{P}^{n} =
\prod_{i=0}^{n-1} [ 1-r_{i} ] \boldsymbol{P}
\;\;\;\;\; ( r_{0} = 0 )
\]
ここで、$r_i$ は各収束段階における荷重増分率であり、0回目の増分率 $r_0$ は0とする。
このまま、引っ張りクラックなどの応力解放が伴う破壊が生じなければ、式(3.18)は山田の方法と同じ結果となる。もし、 $(k- 1)$ 回目に解放カ $\boldsymbol{F}^{k-1}$ が発生した場合、その解放力を残りの荷重量に式(3.19)のように加え合わせる。
\[{\rm (3.19)}
\boldsymbol{P}^{n} =
\prod_{i=0}^{n-1}[1-r_{i}]\boldsymbol{P}
+ \sum_{k=1}^{n} \left( \prod_{i=k}^{n}[1-r_{i}]\boldsymbol{F}^{k-1} \right)
\]
ただし、$k$ 回目において解放力が発生しなければ $\boldsymbol{F}^k=0$ とする。
このようにして、初めに与えた荷重と解放力をすべて使い切るまで繰り返し計算を行う。このときの荷重増分率の合計 $r_{TOTAL}$ は、
\[{\rm (3.20)}
r_{TOTAL} = \sum_{k=1}^{n} \left( \prod_{i=0}^{k-1}[1-r_{i}] \right) r_{k}
\]
によって計算することができ、$r_{TOTAL}$ が1になったとき、解は収束したものと見なすことができる。図3.23は残りの荷重量を単位化し図化したものである。
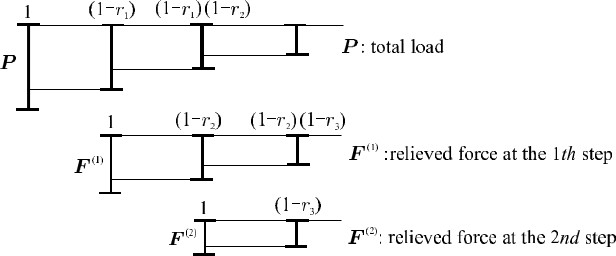
$\hspace{10em}$図3.23 作用荷重
上段が初めに作用した荷重 $\boldsymbol{P}$ に対するもので、中段は第1ステップ目に生じた解放力、下段は第2ステップで生じた解放力である。最終的に破壊箇所が無くなると、式(3.20)における $r_k$ が1となりすべての荷重を使い切ったことになる。このように、本非線形解析法では収束過程において解放力が残りの荷重に含まれているため、厳密な意味で応カーひずみ関係を満足しているとはいえないが、すべての荷重を使い切ったときは荷重レベルに応じた破壊パターンを得ることができる
以上のアルゴリズムを流れ図によって示したものが図3.24 である。圧縮破壊などを考慮したい場合も同様な手順により荷重増分率を考慮すれば可能である。また、軸対称問題についても円周方向の応力に対する荷重増分率 を考慮することによって同様なアルゴリズムを作ることができる。
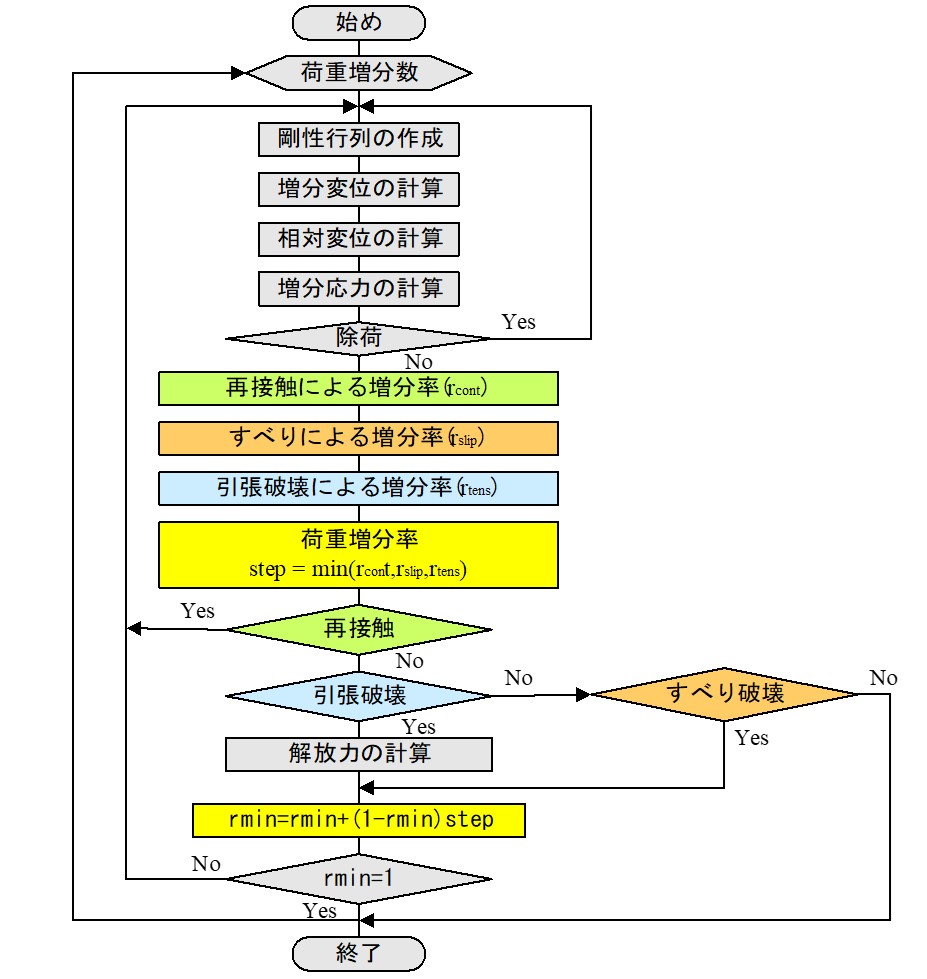
$\hspace{6em}$図3.24 解析の流れ