土の支持力問題は安定解析の一つとして極限解析の立場に立ち、古くから研究されてきた。初期の支持力論は土圧の釣り合いから簡易式を誘導し実用公式として用いるといった、いわゆる「すべり線」の概念に触れないものである。その後、すべり線の概念がRitterによって導入され、基礎幅の影響などが支持カ公式に取り入れられるようになった。1921年、金属塑性論の土の支持力問題に対する応用例として、浅い帯状基礎の極限支持力について発表したPrandtlの理論も支持力論に大きな発展をもたらした。Terzaghiによる自重を考慮した極限支持力に関する研究は現在でも利用されている。また、深い帯状基礎に関するMeyerhofの研究やSokolovskiiによる著書もよく知られている。コンピューターの発達により、最近ではKotter式の数値計算を行い、すべり線場や支持力を求めることも行われている。
これらの研究はいずれも支持力に着目している。一方、欧米諸国と異なり、我が国の地盤は軟弱な場合が多く、構造物の沈下量が問題となるケースも度々見受けられる。杭や直接基礎の耐力が極限支持力のみならず、許容沈下量からも決定されることを考えると、変形に関する定性的あるいは定量的な挙動を掴むことも大切であろう。また、時間の経過に伴って沈下量が増加するといった現象も考えられるため、時間依存に対する考察も必要である。
このように、単に支持力解析といっても多くの問題が含まれている。本節ではこれらの問題のうち、荷重(支持力)と定性的な変形に着目し、川井モデルによる離散化極限解析を行う方法について説明する。以下に支持力問題の一般的な解析上の注意事項をまとめておく。
(1)解析領域
川井モデルによる離散化極限解析法も有限要素法と同様、領域型解析法の1つであるため、
図4.1 に示すよう、閉じた解析領域を設定する必要がある。このため、得られる解に境界の影響が含まれるのを避けることはできない。しかし、川井モデルではメカニズムを形成するすべり線の塑性仕事を評価して極限荷重を求めているため、そのすべり線が領域内に含まれていれば少なくとも支持力値に関しては領域の広さに関係しない。Kotter式によれば、載荷重の傾斜角が小さく、内部摩擦角が $30^{\circ}$ 前後であるなら、すべり線の横方向の広がりは基礎幅の3倍から4倍程度となる。もし、内部摩擦角が $0^{\circ}$ で、自重がなければ基礎幅と同じ広がりになる。
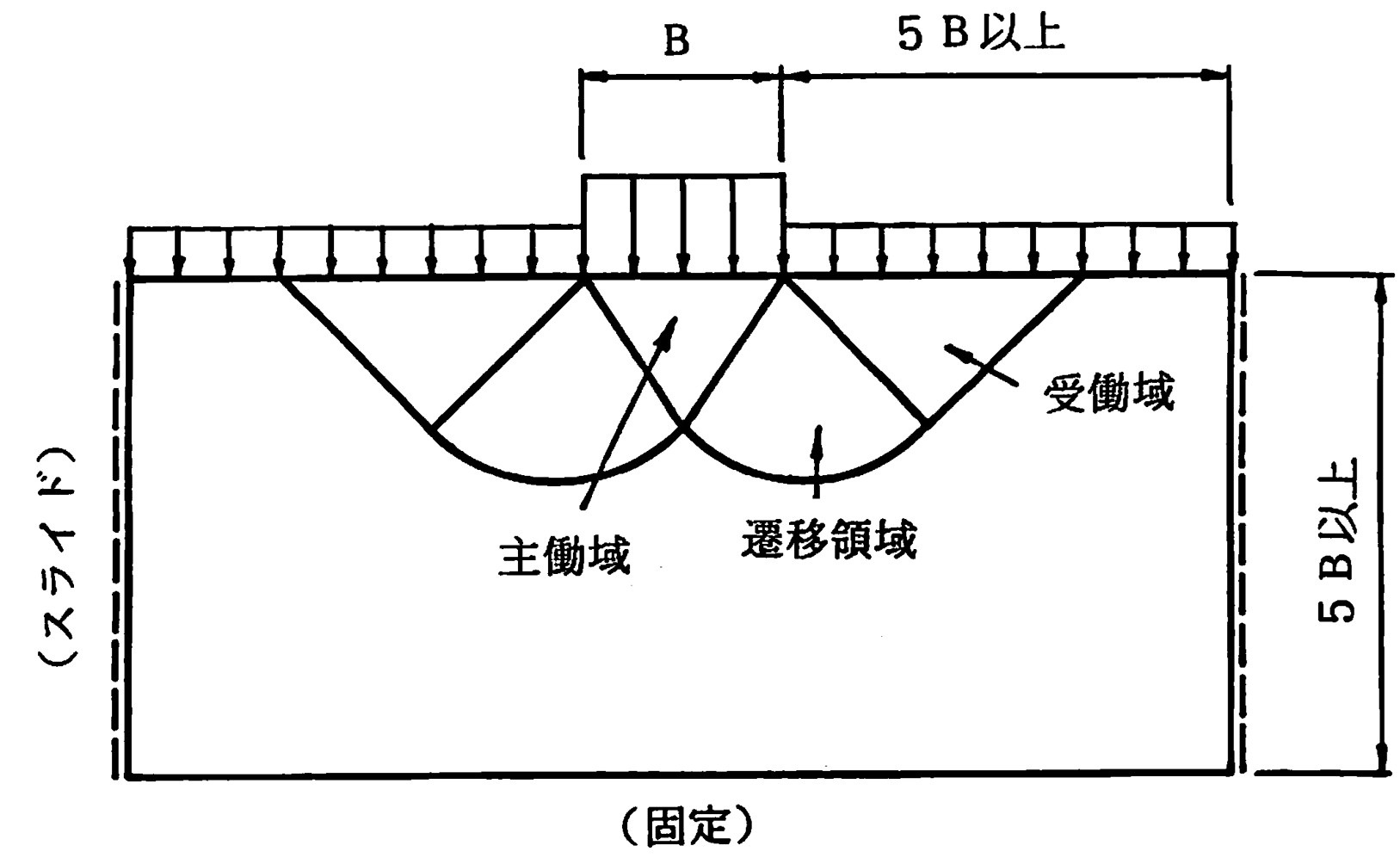
$\hspace{5em}$図4.1 支持力問題の解析領域
一方、テスト・ピット内における平板載荷試験によって地盤の許容鉛直支持力を求める場合、上載荷重の影響が入らないように、粘性土の場合、基礎幅の1.5倍、ゆるい砂の場合2.5倍、締まった砂の場合4倍以上テスト・ピットの内壁から離すよう道路橋示方書(下部構造編)に記載されている。これらのことを考慮し、定性的な変形モードを掴もうとするのであるなら、領域幅は、
図4.1に示すよう、最低でも基礎幅の5倍程度はとっておく必要があるだろう。ただし、主たるすべり線が境界に達するようであれば、さらに領域を広げる必要がある。
次に深さ方向について考えてみよう。道路橋示方書(下部構造編)では、地盤の変形係数を検討する場合、その影響範囲として深さ方向に基礎幅の3倍以上調べなければならないということが記載されている。また、極限支持力から考えた場合、あまり浅いとポンチの押し込みのようなすべり線パターンとなり境界の影響が顕著に現れてしまう。極限解析において自重を無視し、内部摩擦角を $0^{\circ}$ とした場合、$(深さ)/(基礎幅)\le 4.37$ であれば、深さの変化にかかわらず同一の崩壊パターンならびに崩壊荷重を与えることがよく知られている。このことから、深さ方向については、最低でも基礎幅の5倍程度とることが望ましい。ただし、明確な支持層があるならば、そこを境界としてもかまわない。
(2)境界条件
境界条件は、一般的に底部を固定、両側面をスライドとすることがよく行われている。特別な理由がない限りこの方法でよい。ただし、川井モデルの場合は境界用の要素に対してこれらの支点条件を施した方がよい。また、載荷板の拘束については、
図4.2に示すよう、3つの状態が考えられる。どの方法を採用するかは、問題に応じて選択すればよい。

$\hspace{1em}$(a) $u,\theta$:固定
$\hspace{2em}$(b) $\theta$:固定
$\hspace{3em}$(c) $u,\theta$:自由
$\hspace{7em}$図4.2 載荷板の拘束
(3)要素分割
要素分割を行う場合、一般的な注意事項は有限要素法とあまり変わらないが、川井モデルでは与えられた要素境界辺上でのみすべりが発生するため、予め想定されるすべり線を幾つか仮定し要素分割に考慮しておく必要がある。支持力問題のすべり線は、
図4.1 に示すよう主働域、受働域とそれらにはさまれた遷移領域から構成されることが多いため、これらを念頭に要素分割を行うと粗い要素分割であったとしてもよい支持力値を得ることができる。
図4.3はA-A断面以下が支持層で、傾斜荷重を受けた場合の要素分割例である。全体的に傾斜方向を中心に要素分割が行われている。
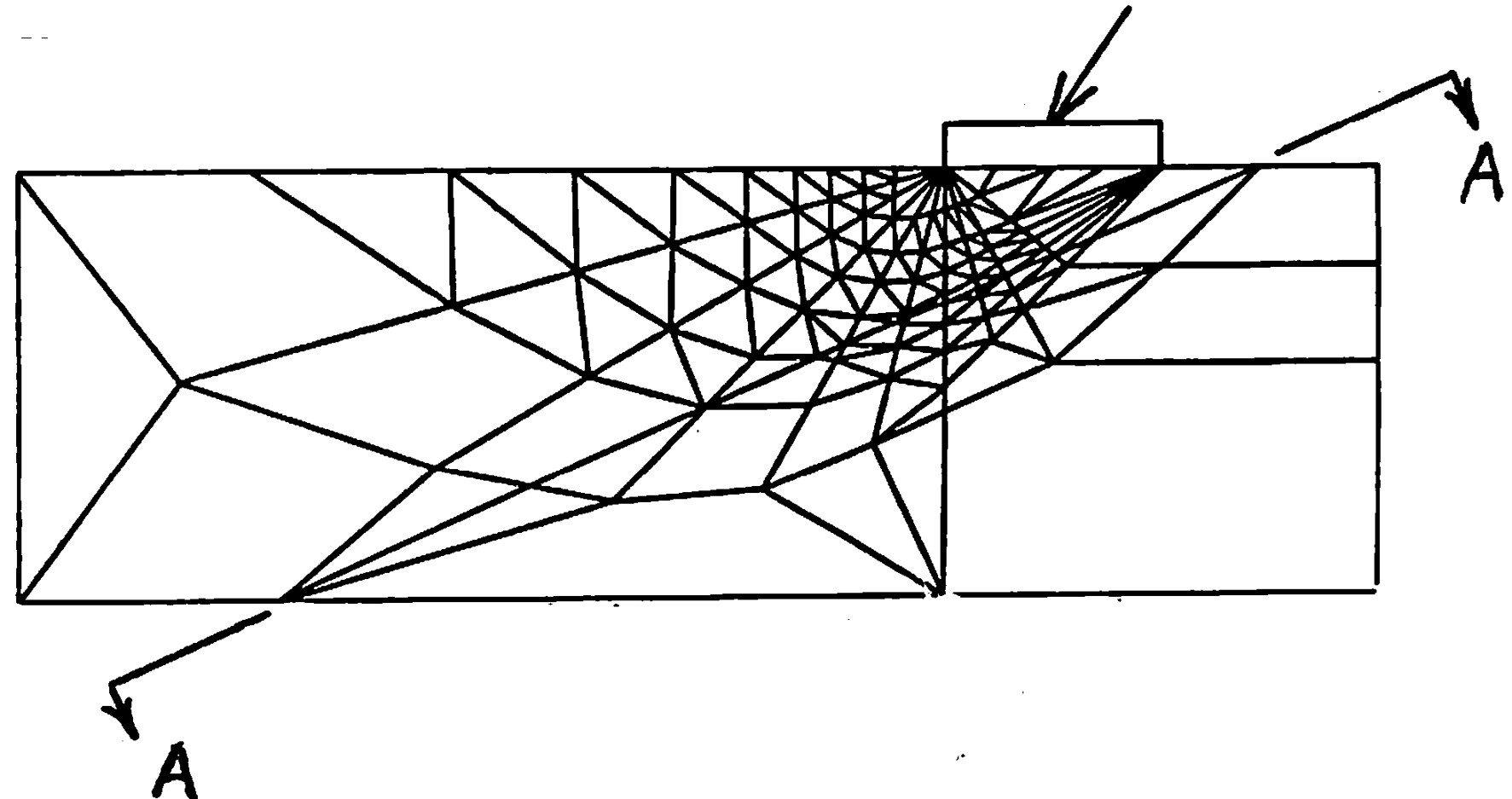
$\hspace{8em}$図4.3 要素分割例
(4)載荷方法
川井モデルの場合、載荷方法として
図4.4に示すよう境界用の要素を通じて行う方法と構造物を一つの要素に分割しそれを通して行う方法の2通りが考えられる。境界用の要素を利用した場合は各境界用の要素間に関連性がないため、
図(a)のような変形モードとなる。傾斜荷重が作用する場合にはこのような載荷方法はあまり適していない。このため、状況にもよるが、
図(b)のように構造物を通して載荷することが望ましい。
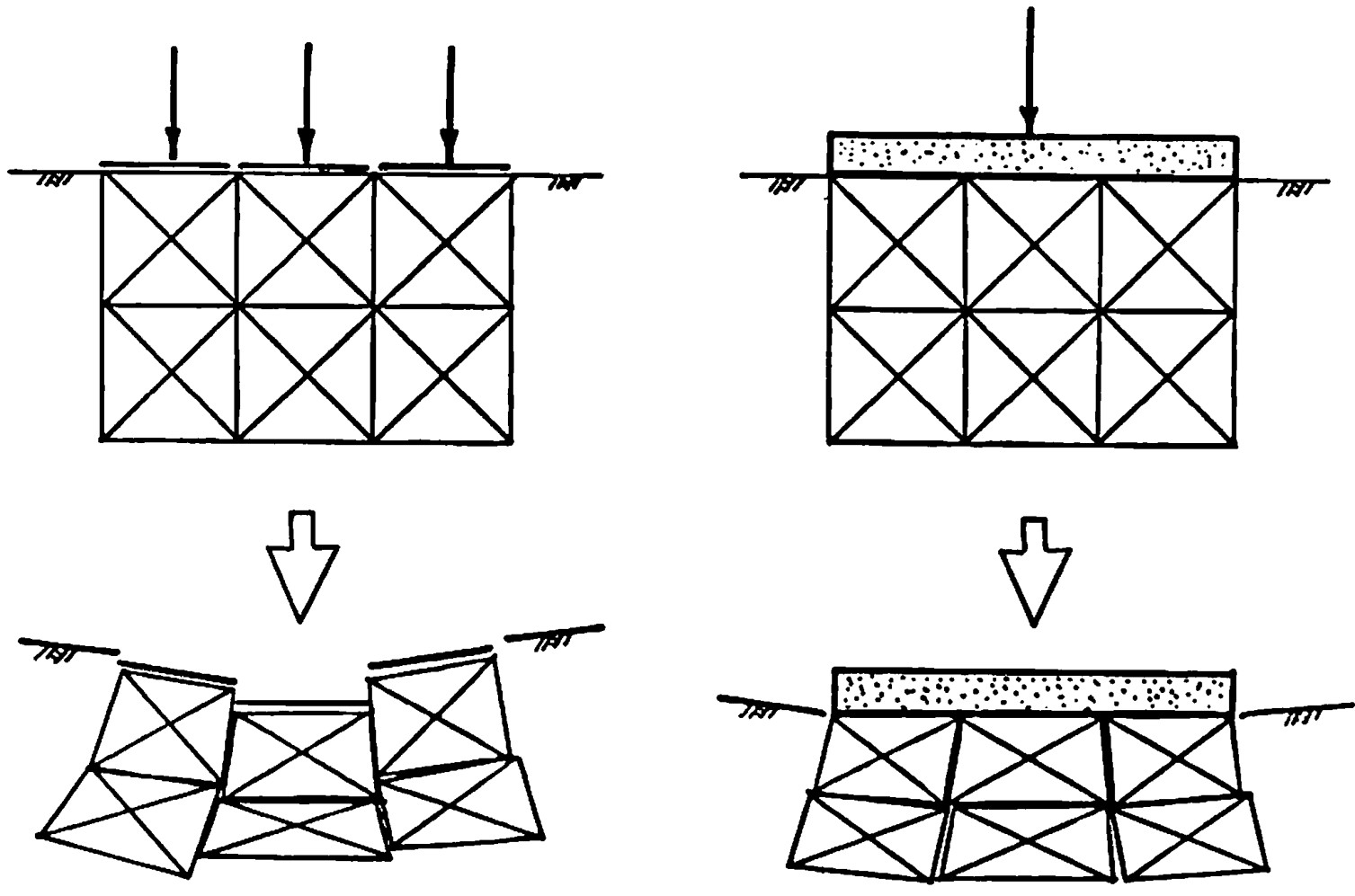
$\hspace{2em}$(a)境界用要素
$\hspace{7em}$(b)構造物
$\hspace{8em}$図4.4 載荷方法
また、自重による初期応力を考慮したりサーチャージなどを考えるならば、載荷順序を考慮し、
図4.5に示すように予めこれらを作用させた後、支持力計算を行わなければならない。特に、非線形解析法として荷重増分法を利用する場合は同時に計算すると自重などにも荷重増分率がかかってくるため、正しい支持力値が求められないこともある。
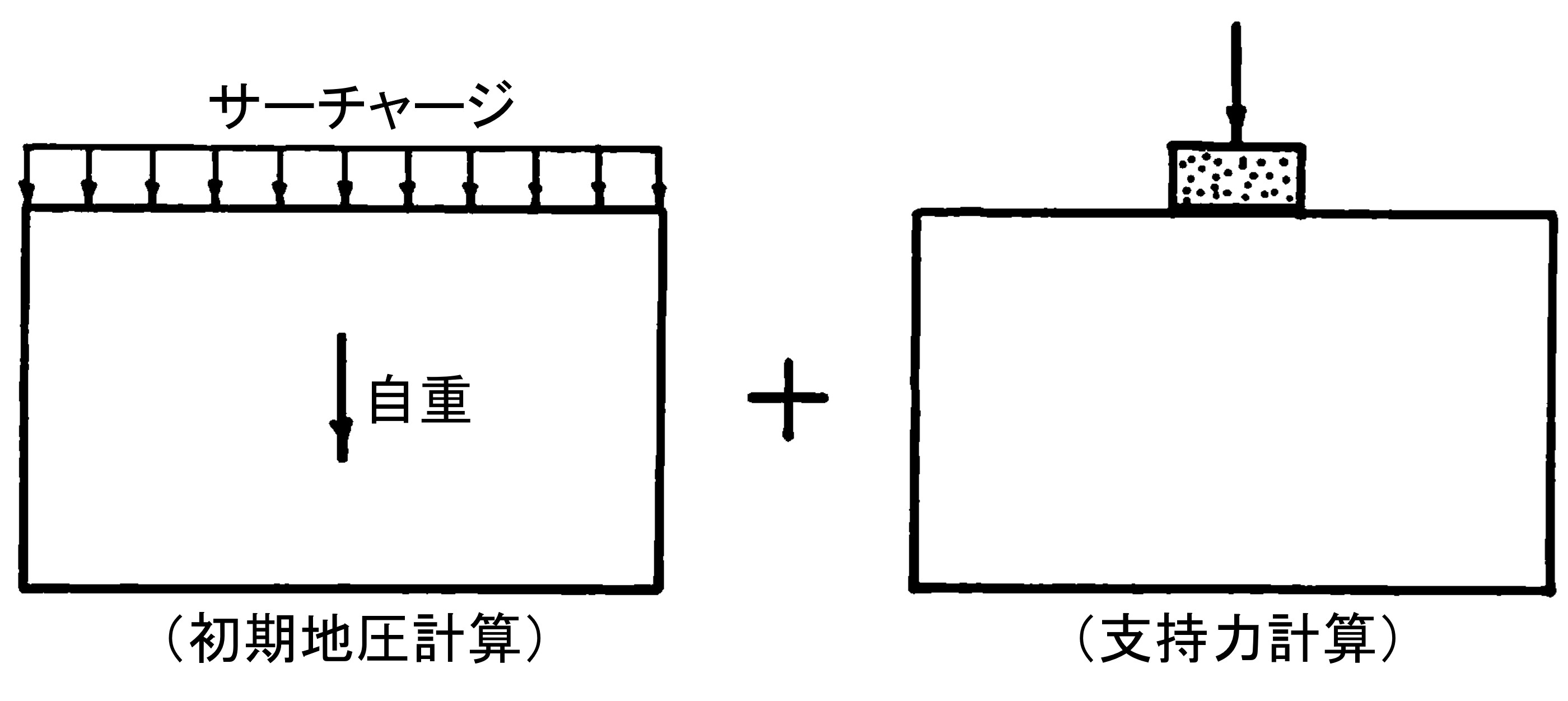
$\hspace{8em}$図4.5 載荷順序
(5)非線形解析法
極限支持力を中心に考える場合、非線形解析法としては
3章で説明した理由
により完全弾塑性体を仮定した荷重増分法における山田の方法を用いた方が簡単である。
ただし、自重やサーチャージなどによる初期地圧を求める場合は反復法による解析を用いても
可能である。また、初期地圧を求めたときに得られた変位については0クリアすることが
よく行われている。
以上のことを考慮した具体的な数値計算例を次節以降に示す。
川井モデルによる支持力問題に対する解析結果の特徴を理解するため、簡単な支持力問題の解析例を示す。
初期地圧を無視した浅い帯状基礎の極限支持力についてはPrandtlらによって理論解が得られている。しかし、土や岩盤などから構成される地盤はそれ自身の重さや、またその生成過程において様々な初期応力を受けている。実際の初期地圧を知ることは極めて困難であり、解析を行う場合、種々の仮定を行わざるを得ない。
自重を考慮した極限支持力として、基礎底部が粗い場合、Terzaghiは次ぎのような公式を与えている。
\[
q_{u} = CN_{c} + ( P_{0} + \gamma_{1}D_{f})N_{q}
+ \frac{\gamma_{2}B}{2}N_{\gamma}
\]
ここで、$N_e、N_q、N_{\gamma}$ は支持力係数であり、以下に示される。
\[\hspace{2em}
N_{q} = \frac{1}{1-\sin \phi '}
\exp\{(\frac{3}{2} \pi - \phi ') \tan \phi ' \}
\]
\[\hspace{2em}
N_{c} = (N_{q}-1) \cot\phi'
\]
\[\hspace{2em}
N_{\gamma} = (N_{q}-1) \tan (1.4 \phi')
\]
Terzaghiはこの支持力公式の $N_{\gamma}$ を、
図4.6に示す $\omega$ に $\omega=\phi$ という仮定を設けて極に働くモーメントの釣り合い式から求めた。
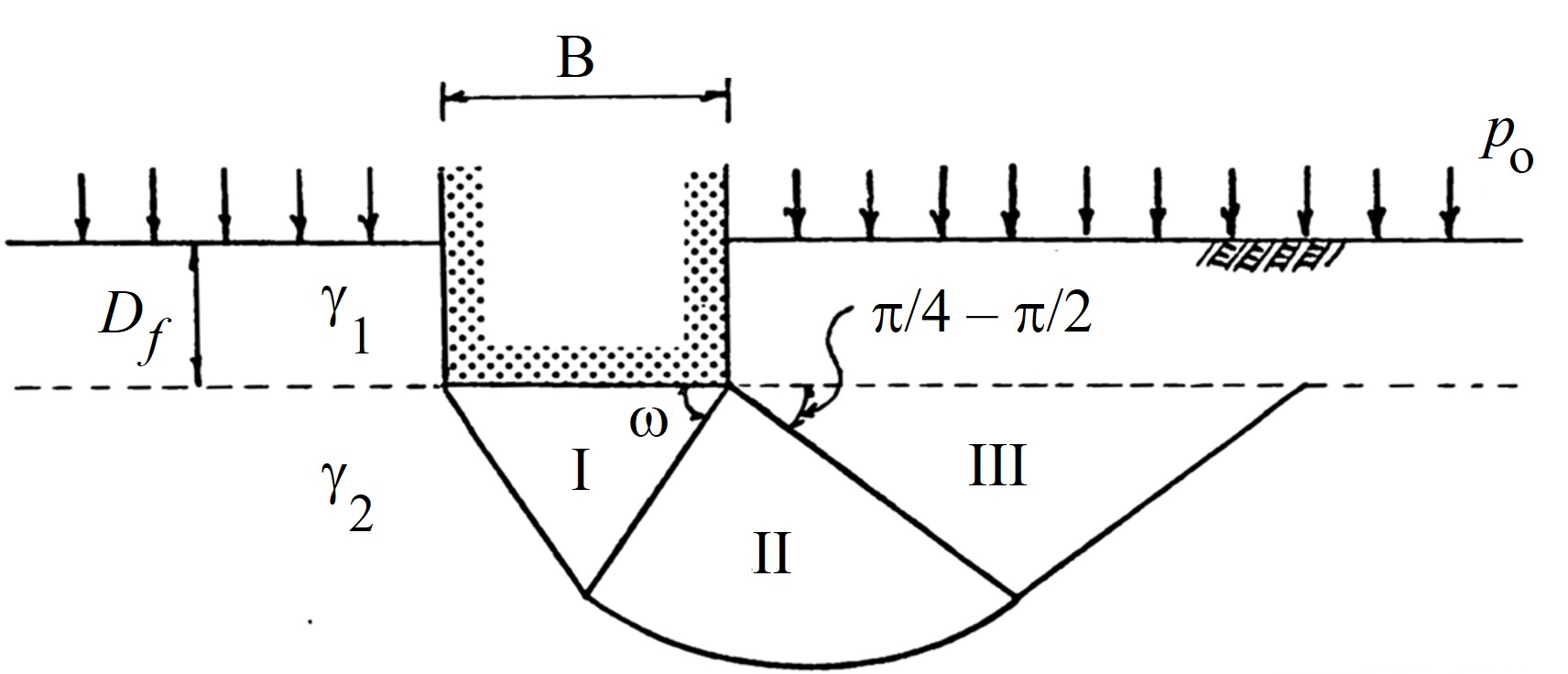
$\hspace{5em}$図4.6 自重を考慮したすべり線場
また、Prandtlは基礎底面が滑らかな場合として、以下のような支持力係数を与えた。
\[\hspace{2em}
\overline{N}_{q} = \frac{1+\sin \phi '}{1-\sin \phi '}
\exp( \pi \tan \phi ' )
\]
\[\hspace{2em}
\overline{N}_{c} = (\overline{N}_{q}-1) \cot\phi'
\]
\[\hspace{2em}
\overline{N}_{\gamma} = \frac{N_{\gamma}}{2}
\]
一方、実験的には基礎底面の粗滑に関係なく $\omega=\pi/4+\phi/2$ に近いことが確かめられている。Caquotは、この実験事実に基づき以下の支持力係数を提案している。
\[\hspace{2em}
{N}_{\gamma}' = 2(N_{q}+1) \tan \phi'
\]
この問題を川井モデルにより解析してみよう。川井モデルでは要素境界辺ですべりが発生する。そこで、先の議論における $\omega$ の値を変えて要素分割を行い、それぞれの極限支持力を求めてみた。
図4.7(a) は $\omega=60^{\circ}$ の場合の要素分割が示されている。また、
図(b)に $\omega=30^{\circ}$、 $\omega=60^{\circ}$ の場合の荷重ー沈下曲線を示す。この結果、$\omega=60^{\circ}$ とした場合の方が、$\omega=30^{\circ}$ より小さめの極限支持力を与えており、Caquotの値に近い。
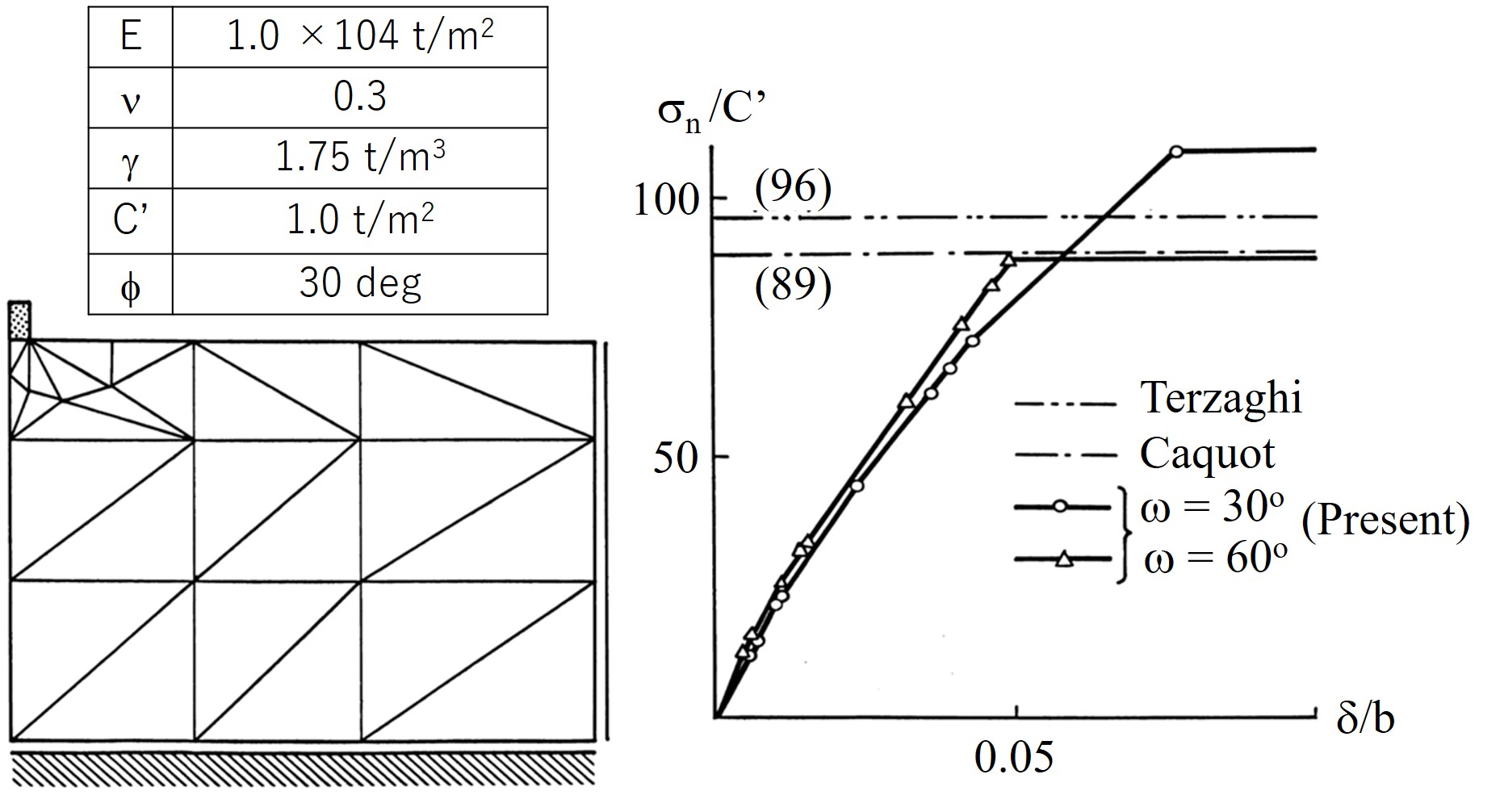
$\hspace{5em}$(a)要素分割$\hspace{8em}$(b)荷重-沈下曲線
$\hspace{6em}$図4.7 自重を考慮した浅い帯基礎の支持力
また、$\omega$ の相違による極限支持力をプロットしたものが
図4.8に示されている。$\omega$ の値が $\omega=60^{\circ}$、すなわち $\omega=\pi/4+\phi/2$ に近づくにつれ極限支持カが低下する傾向が現れている。
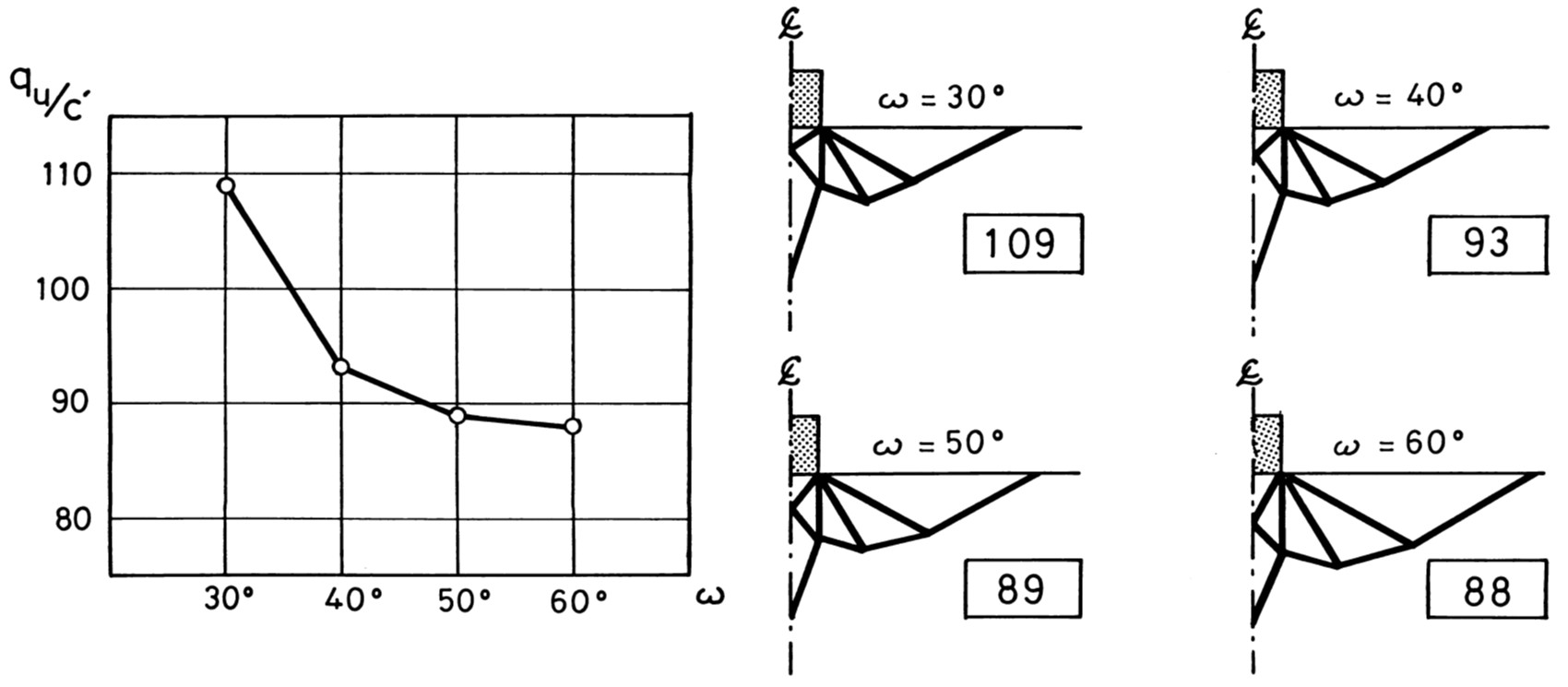
$\hspace{6em}$(a)極限支持力$\hspace{8em}$(b)すべり線
$\hspace{10em}$図4.8 $\omega$ の相違による極限支持力
このように、川井モデルによる極限支持力は要素分割に左右されるが、一方では要素分割に正しいすぺり線が含まれていると簡単な要素分割でより正確に極限支持力を求めることができる。このことが、川井モデルの利点の一つであり、また不利な点ともなっている。
地表面が水平で、均一の材料から構成される地盤の支持力は極限解析により理論的に求められる場合が多い。しかし、実際の地盤は複雑な地層から構成されているため簡単に極限支持力を求めることができない。ここでは、このような種類の違う材料から構成されている地盤の支持力に関する解析を行い、実験結果と比較する。
図4.9は上層が砂層、下層が粘土層で構成される2層系の地盤を表している。この2層地盤における実験結果と川井モデルによる解析結果を比較してみよう。実験では平面ひずみ条件のもと、上載圧 $1.0 {\rm kgf/cm^2}$ を図のように作用させている。解析では実験条件を考慮し、図に示すような材料定数ならびに上載圧を設定した。ただし、土の自重は無視している。非線形解析法は荷重増分法における山田の方法を利用し、破壊条件はモール・・クーロンの条件を用いた。また、応カーひずみ関係は完全弾塑性としている。載荷の順番は、上載圧を作用させ初期応力を求めた後、支持力としての荷重を作用させている。
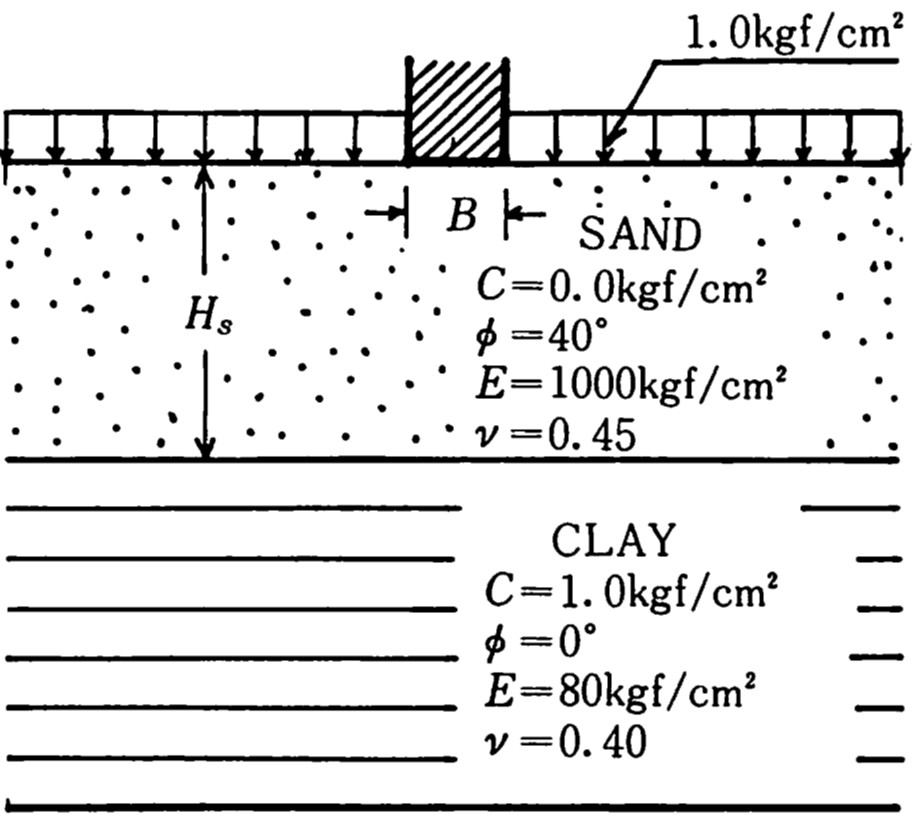
$\hspace{2em}$図4.9 2層系地盤の設定条件
川井モデルの場合、要素分割辺上でのみすべりが発生する。しかし、このように複雑な問題の場合、予め破壊するであろう特定のすべり線を予測することは難しい。そこで、考えられるすべり線を幾つか想定し、
図4.10 に示すようにそれらを含む要素分割を行っておくことが必要である。川井モデルによる離散化極限解析ではこれらの中から最良のすべり線パターンを計算する。
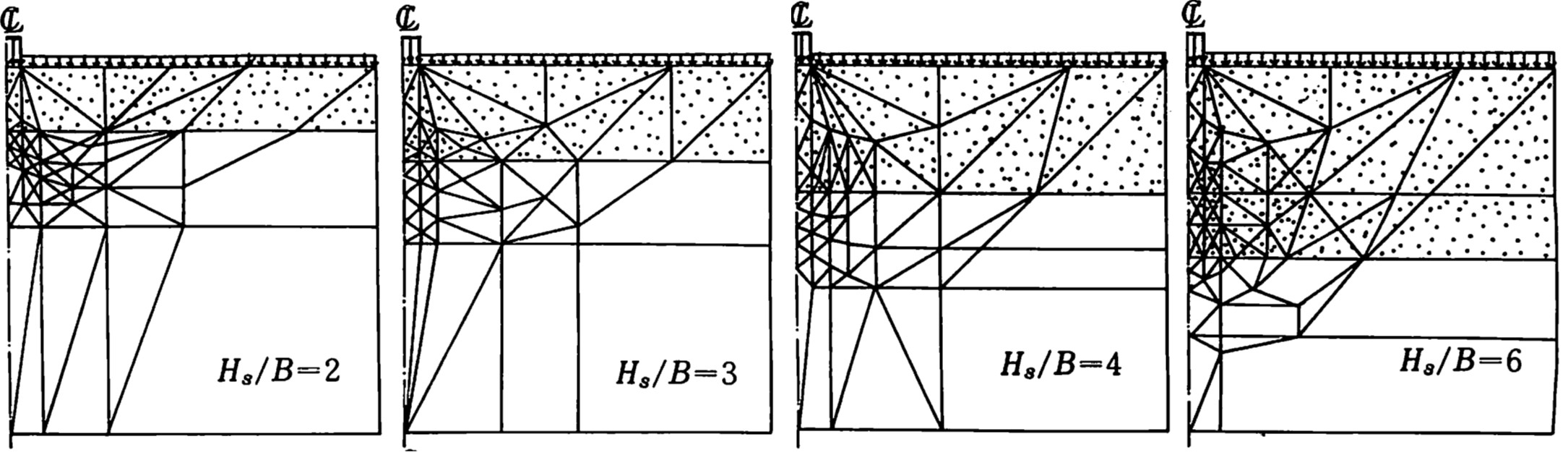
$\hspace{9em}$図4.10 2層系地盤の要素分割例
図4.11はこのようにして求められた破壊パターンを示したものである。
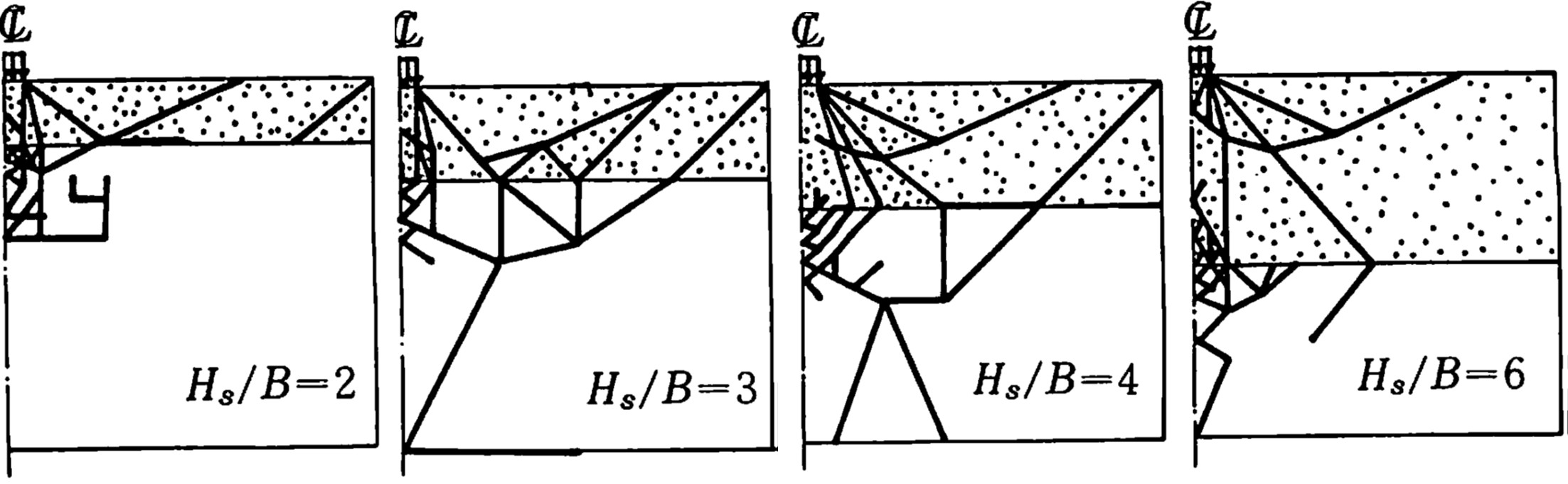
$\hspace{8em}$図4.11 すべり線発生状況
また、このときの荷重一沈下曲線を
図4.12に示す。
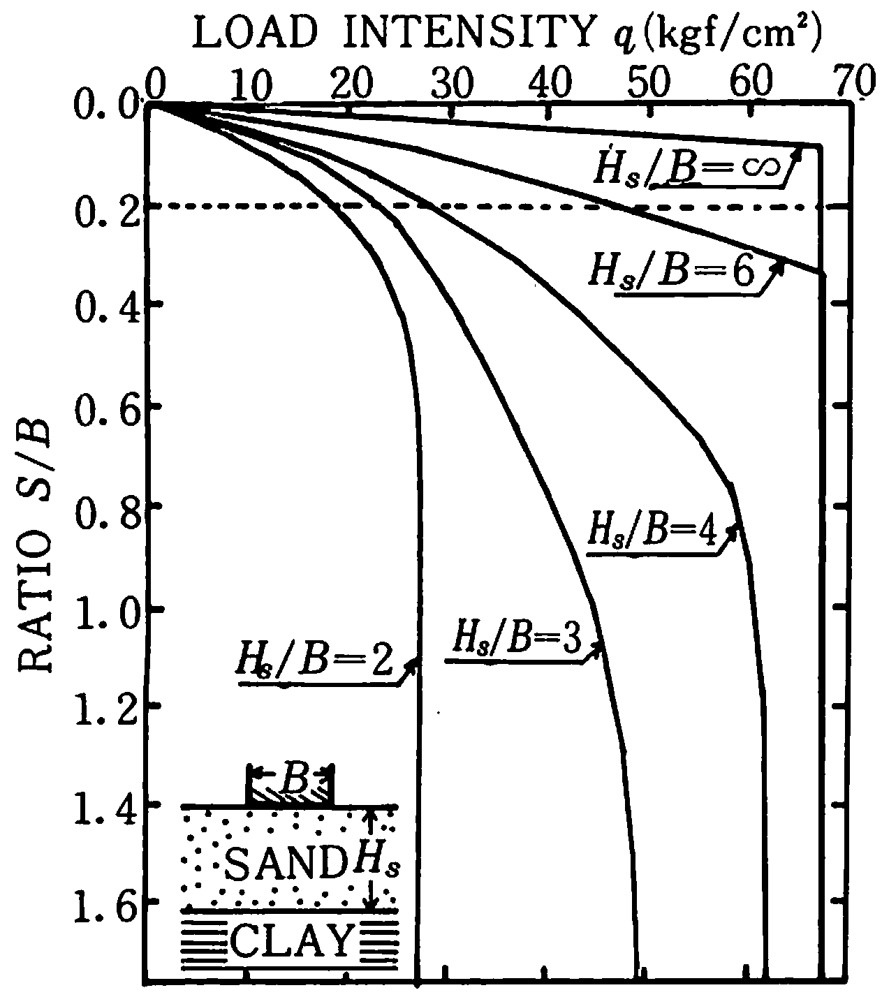
$\hspace{3em}$図4.12 荷重-沈下比曲線
次に、これらの結果を利用し、要素分割を単純化することによって破壊荷重の最小化を試みた。
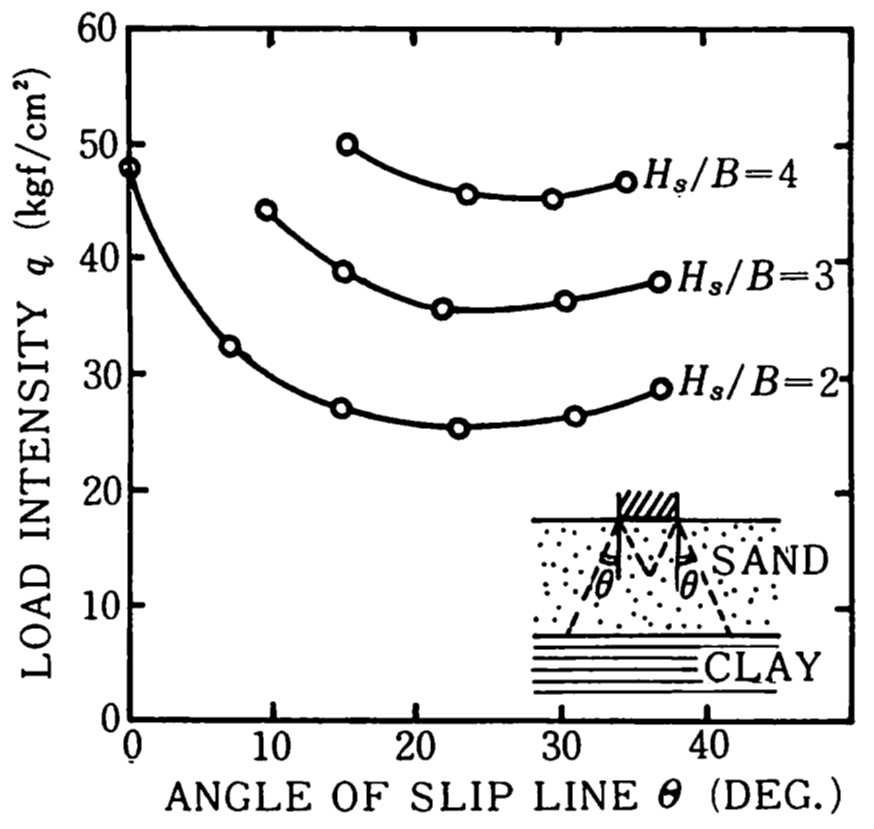
図4.13は単純化された要素分割例を示しており、図中の $\theta$ をパラメーターとして幾通りかの計算を行った。
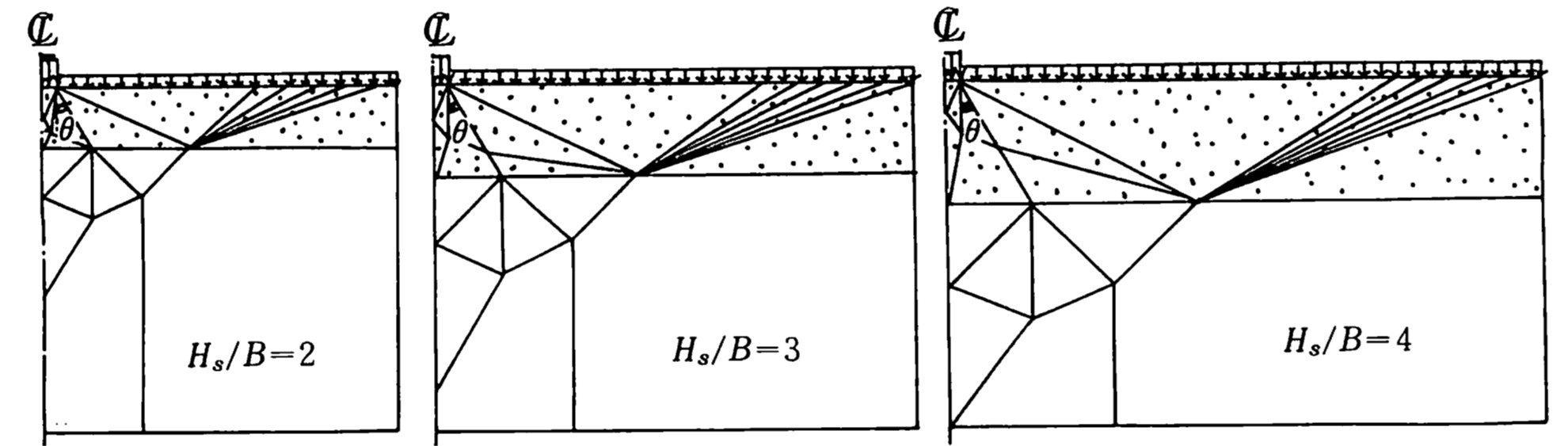
$\hspace{10em}$図4.13 単純化された要素分割例
図4.14は横軸に $\theta$、 縦軸に破壊荷重をとり、これらの計算結果を整理したもので、崩壊荷の最小値を与える角度 $\theta$ は砂層厚の変化にもかかわらず $20^{\circ}~30^{\circ}$ の間にあることがわかる。
$\hspace{6em}$図4.14 $\theta$ と破壊荷重
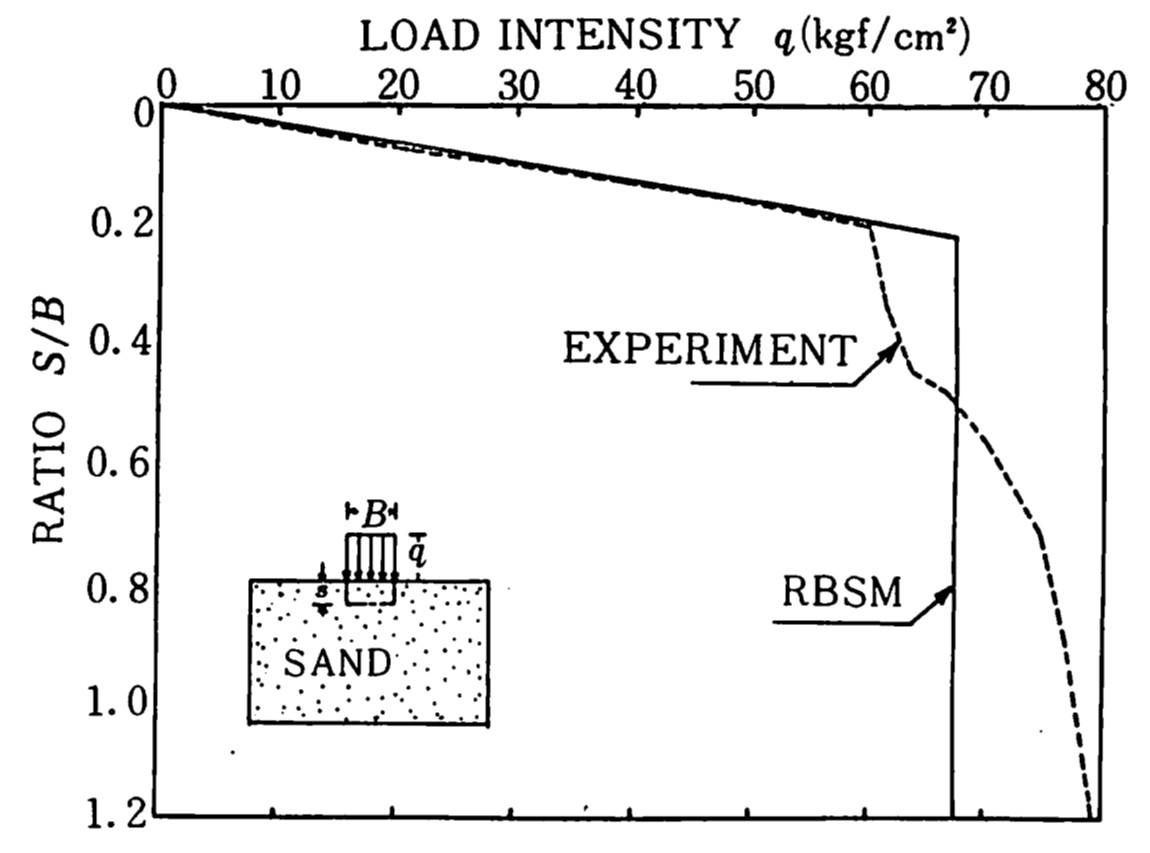
実験と比較するため、川井モデルによる砂層のばね定数を
図4.15に示すよう実験結果から逆算し、先の計算で求まった最小崩壊荷重を与える角度 $\theta$ を用い再度計算を試みた。解析に用いた材料定数を
表4.1 に示す。
$\hspace{1em}$図4.15 砂層のみの場合の荷重-沈下比曲線
表4.1 再計算に用いた材料定数
| $H_s/B$ |
砂 層 |
粘 土 層 |
| $\hspace{2em}C \\ {\rm (kgf/cm^2)}$ |
$\phi(度)$ |
$\hspace{2em}E \\ {\rm (kgf/cm^2)}$ |
$\nu$ |
$\hspace{2em}C \\ {\rm (kgf/cm^2)}$ |
$\phi(度)$ |
$\hspace{2em}E \\ {\rm (kgf/cm^2)}$ |
$\nu$ |
| 2 |
0 |
40 |
389 |
0.45 |
0.67 |
0 |
80 |
0.4 |
| 3 |
0 |
40 |
389 |
0.45 |
0.73 |
0 |
80 |
0.4 |
| 4 |
0 |
40 |
389 |
0.45 |
0.65 |
0 |
80 |
0.4 |
図4.16は、実験(破線)および解析(実線)による荷重一沈下曲線を示したものである。どの解析結果とも要素分割が少ないわりには実験結果と良い一致を示している。川井モデルにおけるばね定数の決定法については現在でも議論が残されているが、このように実験から推定するのも一つの方法である。
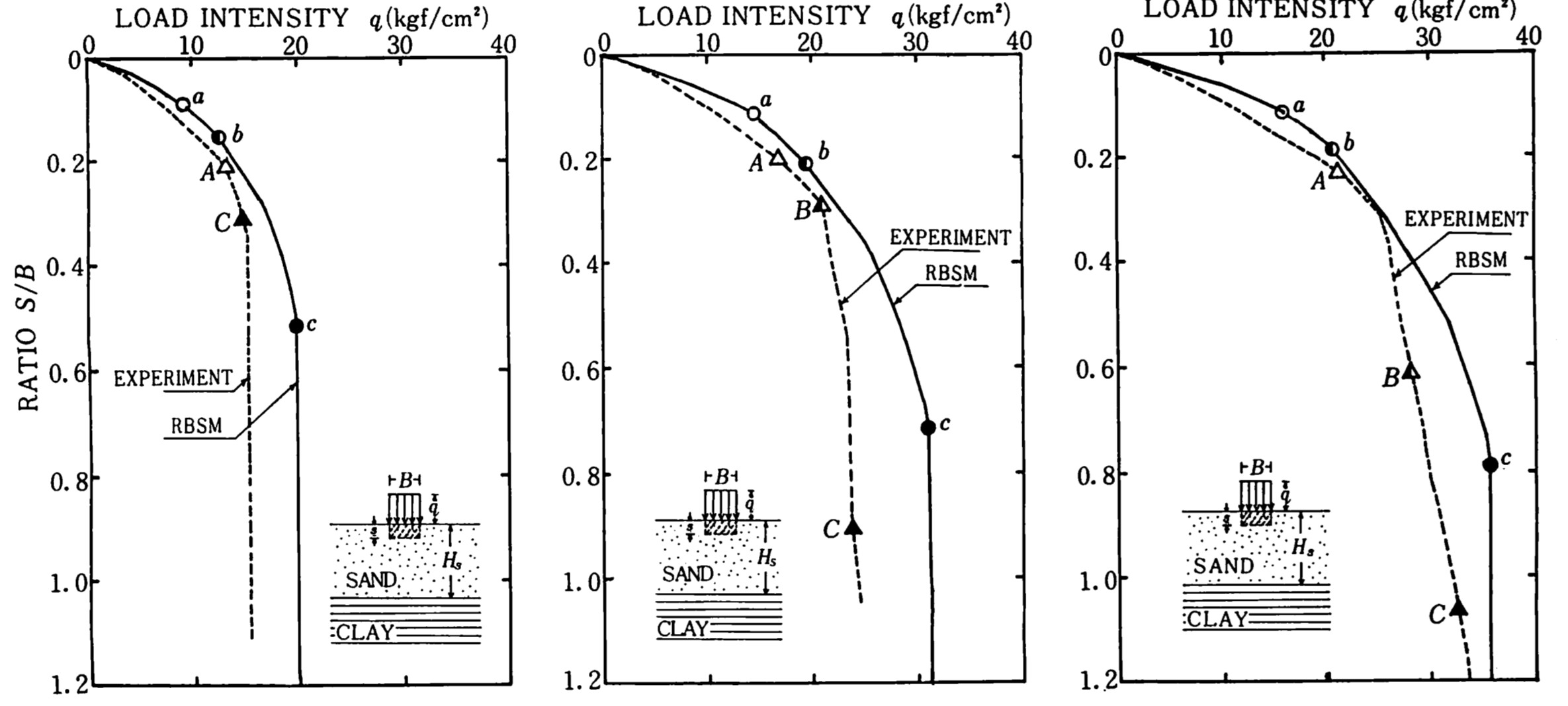
$\hspace{5em}$(a)$H_s/B=2$
$\hspace{5em}$(b)$H_s/B=3$
$\hspace{6em}$(c)$H_s/B=4$
$\hspace{10em}$図4.16 再計算後の荷重-沈下比曲線
次に、
図4.16において代表的な点a、b、c(実験はA、B、C)をとり、これらの応力状態におけるすべり線の状況を比較してみたものが
図4.17に示されている。aの状態は砂層に発生したすべり線が粘土層に到達した状態であり、bでは粘土層ですべり線がさらに発達し、次のcでは粘土層のすべり線が砂層に到達して破壊状態になっている。両者を見比べてみると若干、実験結果の方がすべり線の発達が遅い。しかし、すべりの発生位置、発生順序は類似していることがわかる。
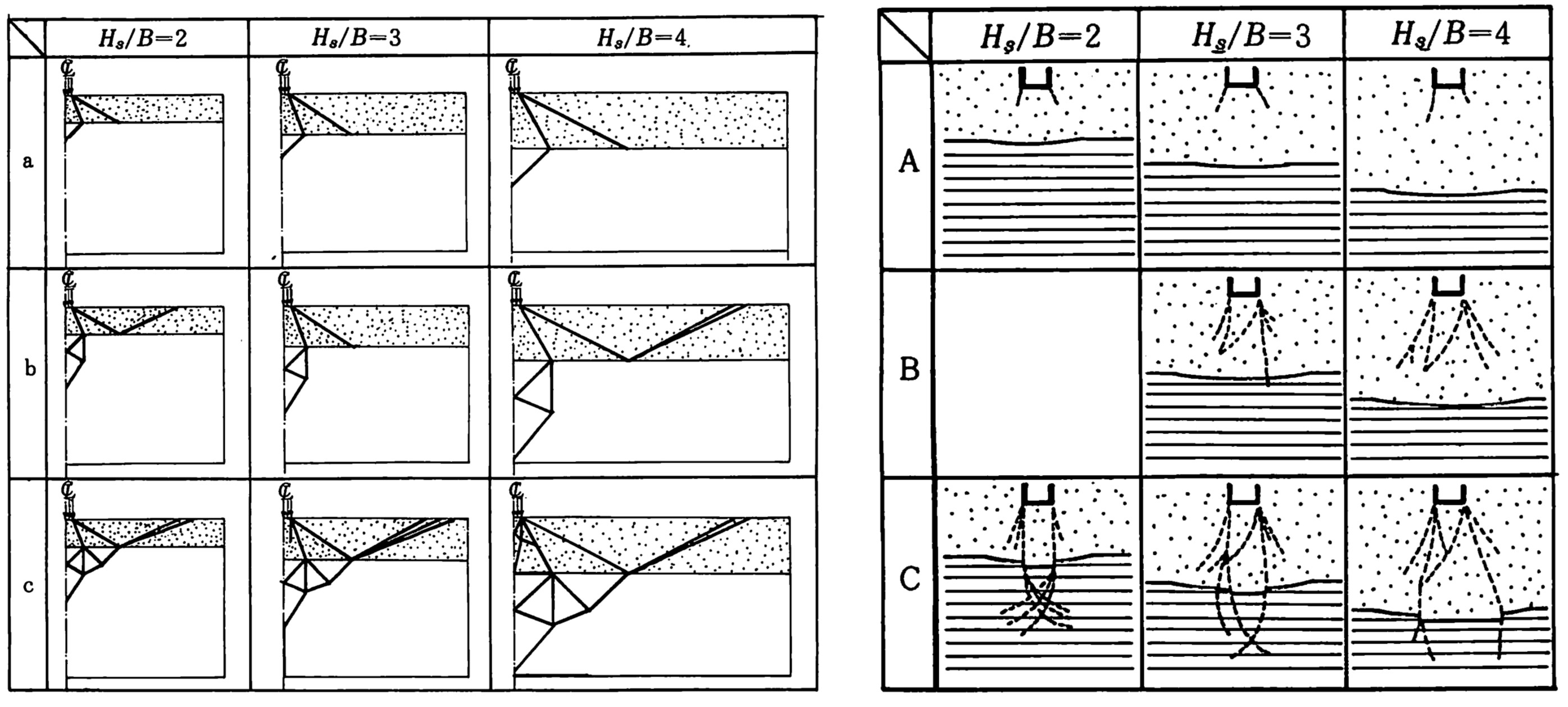
$\hspace{8em}$(a)解析結果
$\hspace{12em}$(b)実験結果
$\hspace{13em}$図4.17 すべり線発生状況
この他にも塩井らは傾斜した2層系地盤の支持力解析を行い良好な結果を得ている。
斜面法肩に構造物を施工するような場合、支持力問題としての検討が必要になる。この場合、すべり線や極限支持力は法面勾配や載荷位置によって左右されるため、水平地盤の場合と大きく異なる。ここでは、このような斜面上の支持力問題に対する解析結果を既往の極限解析解や実験結果と比較してみる。
均ー地盤の法肩にある帯基礎に対して、土の自重を考慮し、上界定理を適用した極限支持力が中瀬らによって求められている。
図4.18は、この基になっている考え方を示した図で、AABEは主働くさび、BCはEを極とする対数ら線、CDは法面に達する直線である。持力公式は主働くさびの底角 $(\omega)$ を $\pi/2+\phi/2$ と仮定し、斜面勾配 $\beta$、斜面肩余裕幅の比 $a$ を用い、過渡領域の角度 $\theta$ をパラメーターとして、$\theta$ に対する極小値を求めることにより導かれている。詳細は文献に譲り、初めにこの極限解析解と川井モデルによる解と比較してみよう。
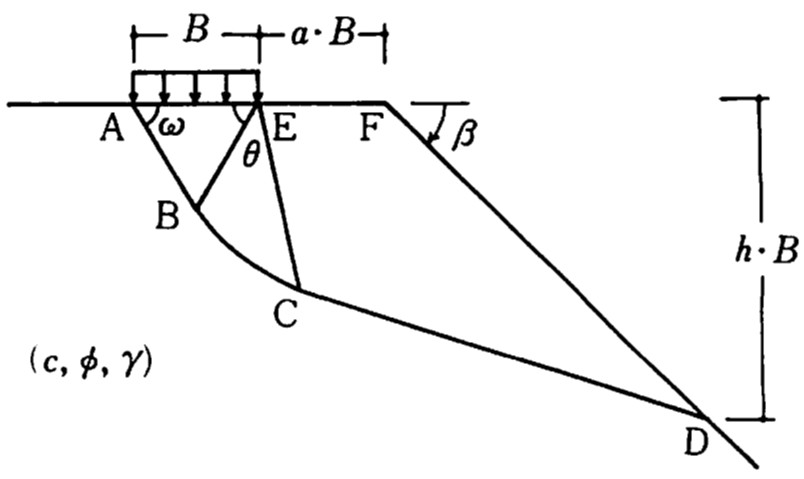
$\hspace{4em}$図4.18 極限解析法におけるすべり線
斜面上の支持力であっても極限荷重を求めるという観点では、非線形解析法として
3章で示した荷重増分法における山田の方法が適している。ここでは、初めにこの初期応力を山田の方法により求め、この値を各ばねに与え、変位をクリアした後、山田の方法により離散化極限解析を行っている。
図4.19は内部摩擦角 $\phi=30^{\circ}$ の場合の要素分割例である。川井モデルでは与えられた要素分割における要素境界辺上でのみすべりを表現するため、解析解と極限支持力のみ比較するという観点では図のような極端な要素分割も可能であり、むしろ合理的である。
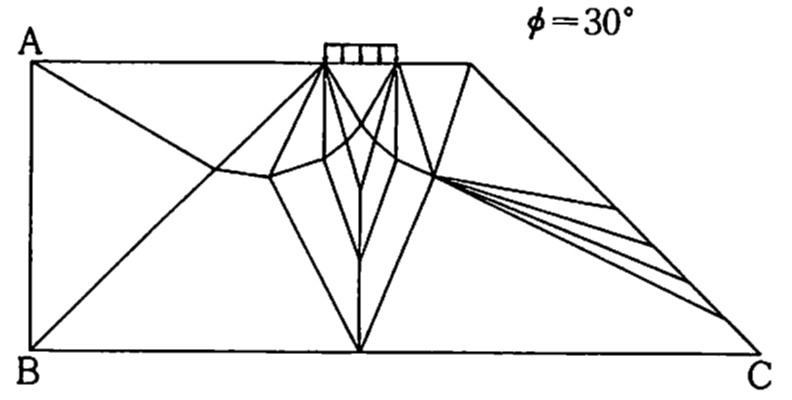
$\hspace{4em}$図4.19 要素分割図 $( \beta=45^{\circ}$、$a=1$)
境界条件は底面BCを固定、側面ABはスライドとし、載荷部の回転を拘束とした。応カーひずみ関係は完全弾塑性で、破壊条件としてはモール・クーロンの条件を用いてる。計算に用いた材料定数は
材料定数
| 弾性係数 $E {\rm (tf/m^2)}$ |
1000 |
| ポアソン比 $\nu$ |
0.45 |
| 粘着力 $C {\rm (tf/m^2)}$ |
5 |
| 内部摩擦角 (度) |
0、 30 |
であり、形状パラ-メータは以下のとおりである。計算はこれらの組み合わせ、計24通りについて行っている。
パラメーター
| $C/\gamma B$ |
25、1 |
| $\beta$ |
$30^{\circ}$、$45^{\circ}$、$60^{\circ}$ |
| $a$ |
0、1 |
図4.20は各ケースにおける最終的な破壊パターンを示した図である。この結果を整理し、支持力値を極限解析解と比較したものが
表4.2に示されている。極端に荒い要素分割でありながら、解析解と良好な一致を示していることが理解できよう。
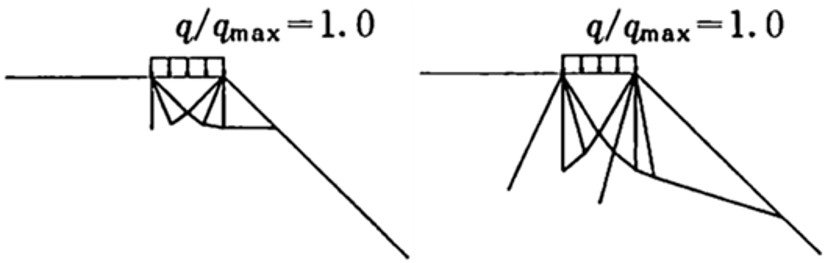
$\hspace{3em}$(a) $\; a=0,\phi=0^{\circ}$
$\hspace{3em}$(b) $\; a=0,\phi=30^{\circ}$
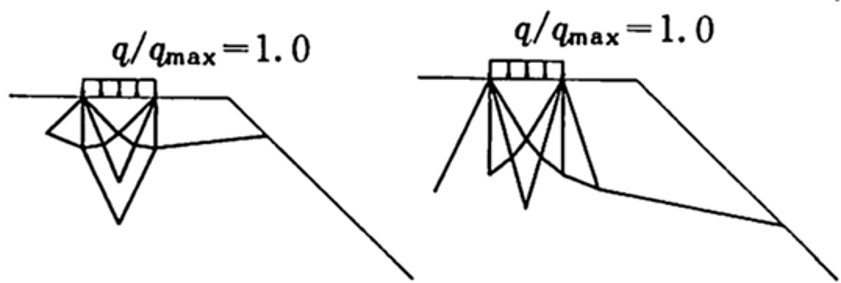
$\hspace{3em}$(c) $\; a=1,\phi=0^{\circ}$
$\hspace{3em}$(d) $\; a=1,\phi=30^{\circ}$
$\hspace{4em}$図4.20 破壊パターン $(C/\gamma B=25)$
表4.2 解析解との比較
| $c/\gamma B$ |
$c \\ {\rm (tf/m^2)}$ |
$\phi \\ ( \circ )$ |
$\beta \\ ( \circ )$ |
$a$ |
$q_{\rm max}{\rm (tf/m^2)}$ |
$ratio$ |
| $RBSM$ |
$Limit \\ Analysis$ |
| 1 |
5 |
0 |
30 |
0 |
19.35 |
19.18 |
1.009 |
| 1.0 |
25.32 |
24.84 |
1.019 |
| 45 |
0 |
6.23 |
15.99 |
1.015 |
| 1.0 |
23.37 |
23.15 |
1.010 |
| 60 |
0 |
12.92 |
12.93 |
0.999 |
| 1.0 |
19.66 |
19.49 |
1.009 |
| 5 |
30 |
30 |
0 |
93.70 |
91.22 |
1.027 |
| 1.0 |
124.22 |
121.93 |
1.019 |
| 45 |
0 |
57.64 |
56.98 |
1.012 |
| 1.0 |
85.78 |
84.93 |
1.010 |
| 60 |
0 |
35.58 |
35.32 |
1.007 |
| 1.0 |
55.43 |
54.87 |
1.010 |
| 25 |
5 |
0 |
30 |
0 |
20.67 |
20.42 |
1.012 |
| 1.0 |
25.77 |
25.02 |
1.030 |
| 45 |
0 |
17.91 |
17.78 |
1.007 |
| 1.0 |
24.51 |
24.11 |
1.017 |
| 60 |
0 |
15.45 |
15.15 |
1.020 |
| 1.0 |
22.51 |
22.73 |
0.990 |
| 5 |
30 |
30 |
0 |
81.46 |
78.93 |
1.032 |
| 1.0 |
97.28 |
94.85 |
1.026 |
| 45 |
0 |
56.39 |
55.75 |
1.011 |
| 1.0 |
75.22 |
74.48 |
1.010 |
| 60 |
0 |
39.07 |
38.77 |
1.008 |
| 1.0 |
58.54 |
57.86 |
1.012 |
斜面高と基礎幅の比 $(H/B)$ がさらに小さくなると、斜面内にあったすべり線は斜面下に移動する。この場合、先の支持力公式は適用できなくなる。一方、$H/B=O$ の場合(水平地盤)についてはTerzaghiによって支持力が求められている。
そこで、これら2つの公式を結ぷ中間の支持力を川井モデルにより求めたものが次の計算例である。以下に計算に用いた諸条件を示す。
材料定数
| 弾性係数 $E {\rm (tf/m^2)}$ |
1000 |
| ポアソン比 $\nu$ |
0.45 |
| 粘着力 $C {\rm (tf/m^2)}$ |
5 |
| 内部摩擦角 (度) |
30 |
パラメーター
| $C/\gamma B$ |
1 |
| $\beta$ |
$45^{\circ}$、$60^{\circ}$ |
| $a$ |
0 |
| $H/B$ |
0, 0.5, 1.0, 1.5 |
また、計算に用いた要素分割の例を
図4.21に、計算によって得られたすべり線状態を
図4.22に示す。
図4.23は横軸に $H/B$、縦軸に極限支持力をとり、それぞれの値をプロットしたものである。斜面高の増加に伴う支持カの減少傾向が比較的良く捉えられている。
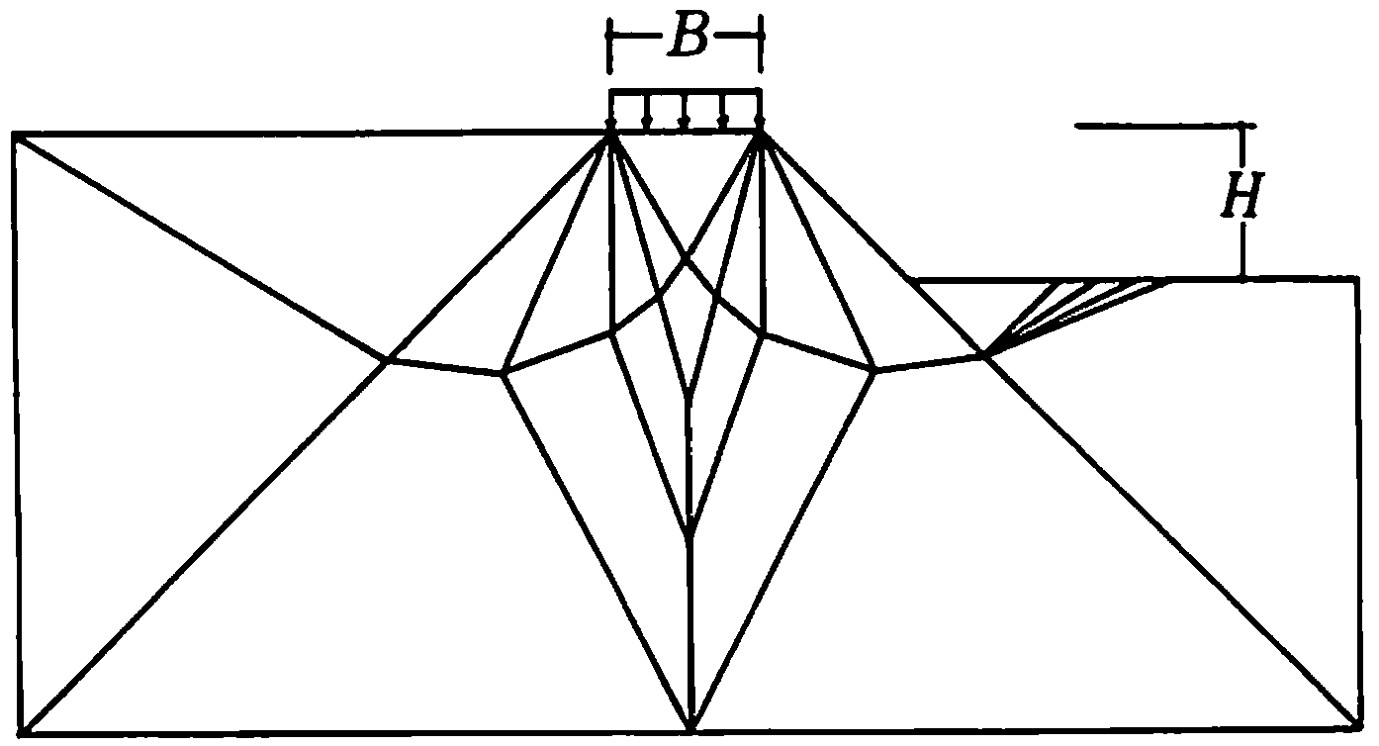
$\hspace{4em}$図4.21 要素分割例 $( H/B=1.0 )$
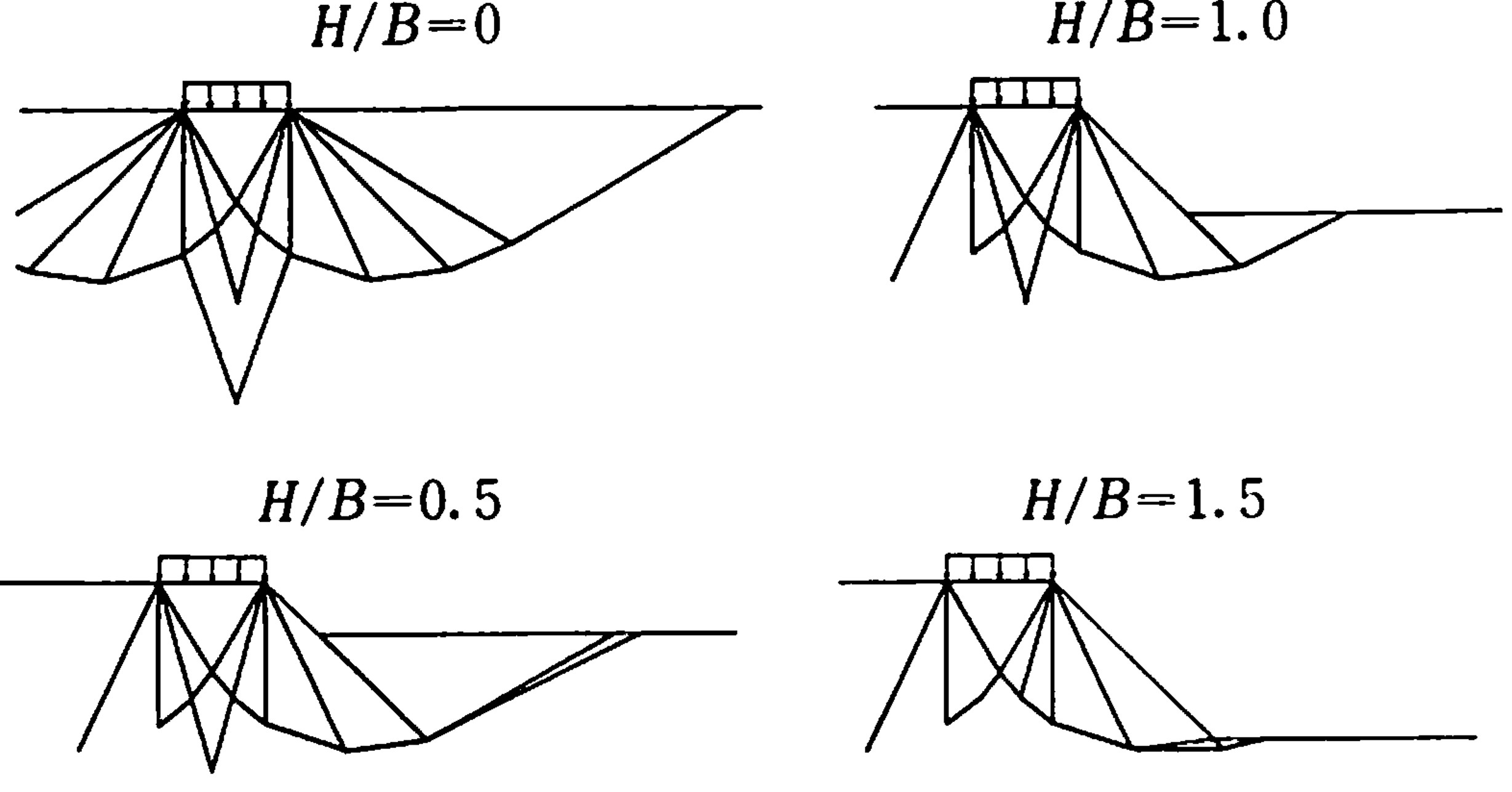
$\hspace{2em}$図4.22 破壊時のすべり線 $( C/\gamma B=1, \beta=45^{\circ} )$
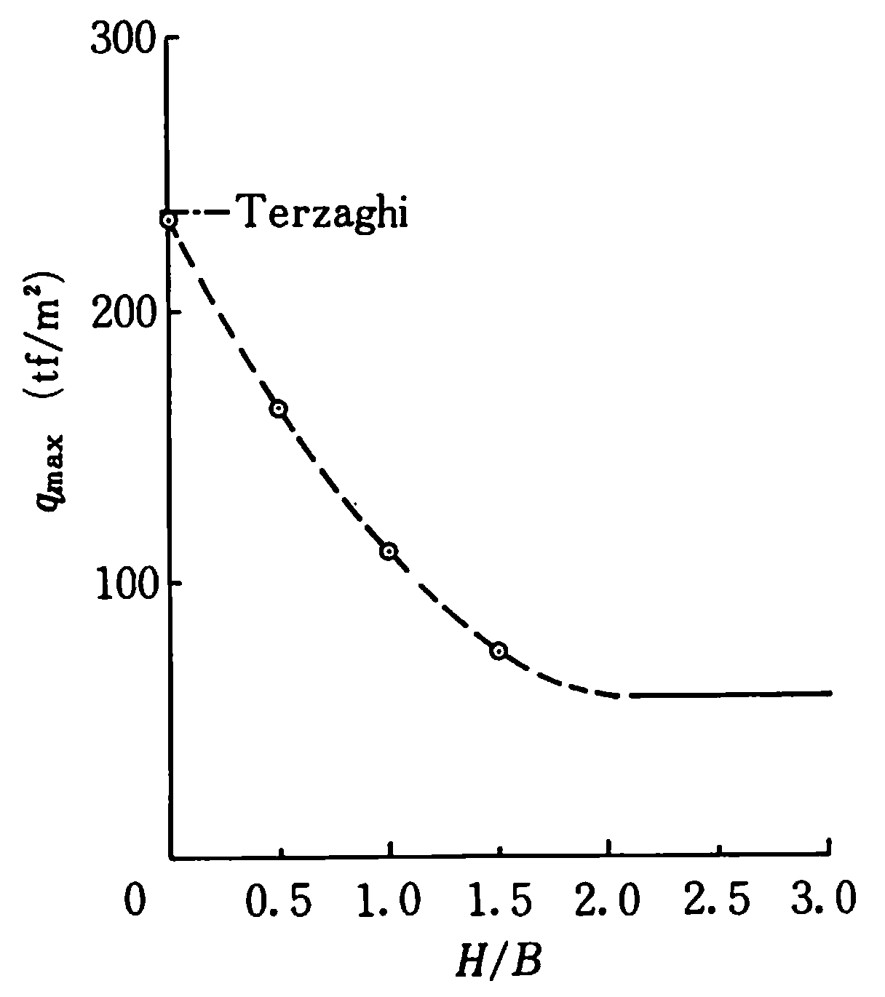
$\hspace{2em}$図4.23 極限支持力の計算結果
次に稲城砂を用いた模型実験による結果と比較した例を示す。解析に用いたモデルを
図4.24に示す。
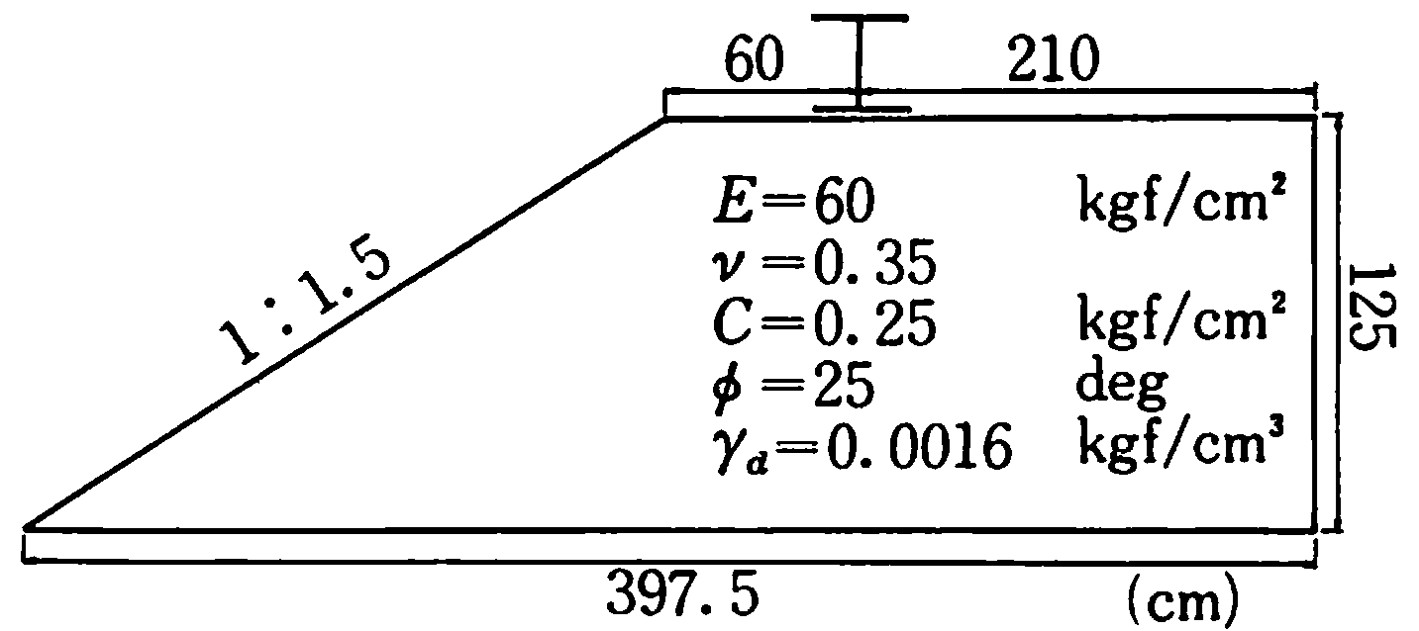
$\hspace{4em}$図4.24 解析に用いた実験モデル
材料定数は文献より、士の単位体積重量 $\gamma_d = 0.0016 {\rm kgf/cm^3}$、内部摩擦角 $\phi = 30^{\circ}$、粘着力 $C = 0.25 {\rm kgf/cm^2}$ とした。また、ポアソン比については平面ひずみ条件下の $K_0$ 圧密を考えることにより
\[\hspace{2em}
\nu = \frac{K_0}{1+K_0}
\]
で表され、Jakyの式 $K_0 = 1-\sin \phi = 0.577$ を用い、$\nu \approx 0.35$ とした。弾性係数 $E$ は三軸圧縮条件下で
\[\hspace{2em}
E = \varepsilon_1 [ \sigma_1 - \sigma_3 - (2 \nu-1)\sigma_3]
\]
となることより、
図4.25に示す三軸試験結果を用い、$\sigma_3 = 0.5 {\rm kgf/cm^2}$における1%の割線弾性係数 $E = 60 {\rm kgf/cm^2}$ とした。ただし、荷重増分法の場合、一般的には接線弾性係数を用いる傾向にある。
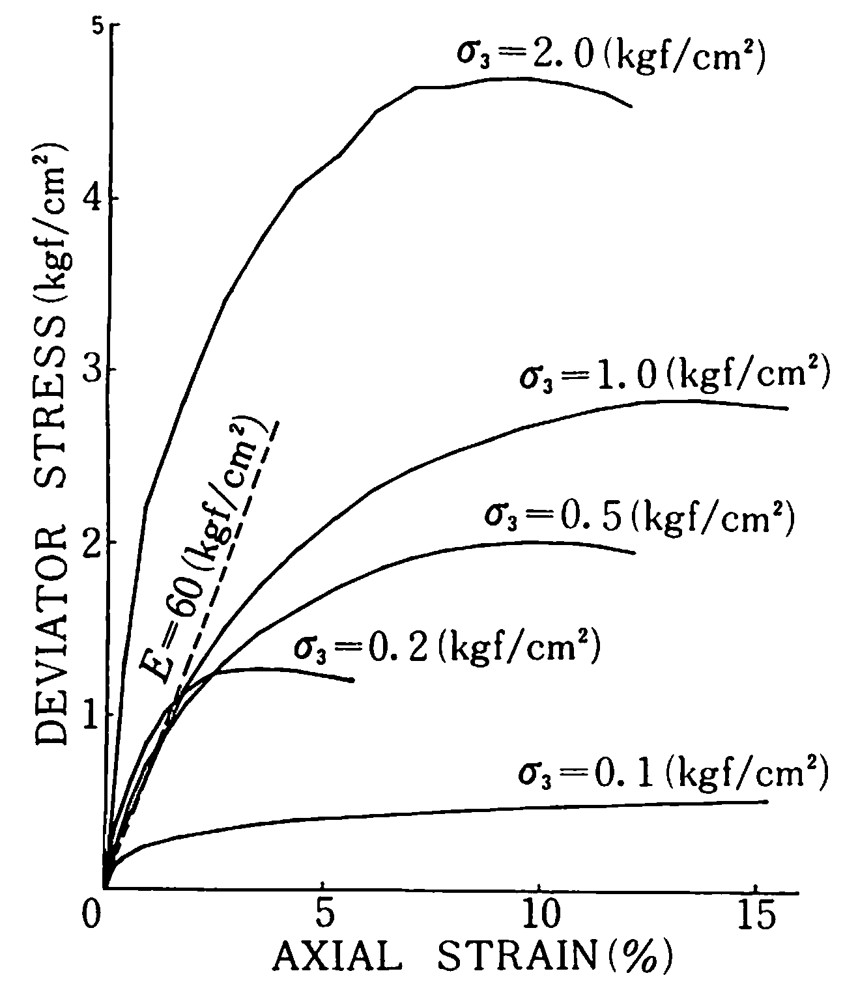
$\hspace{4em}$図4.25 三軸試験結果
図4.26に解析に用いた要素分割が示されている。
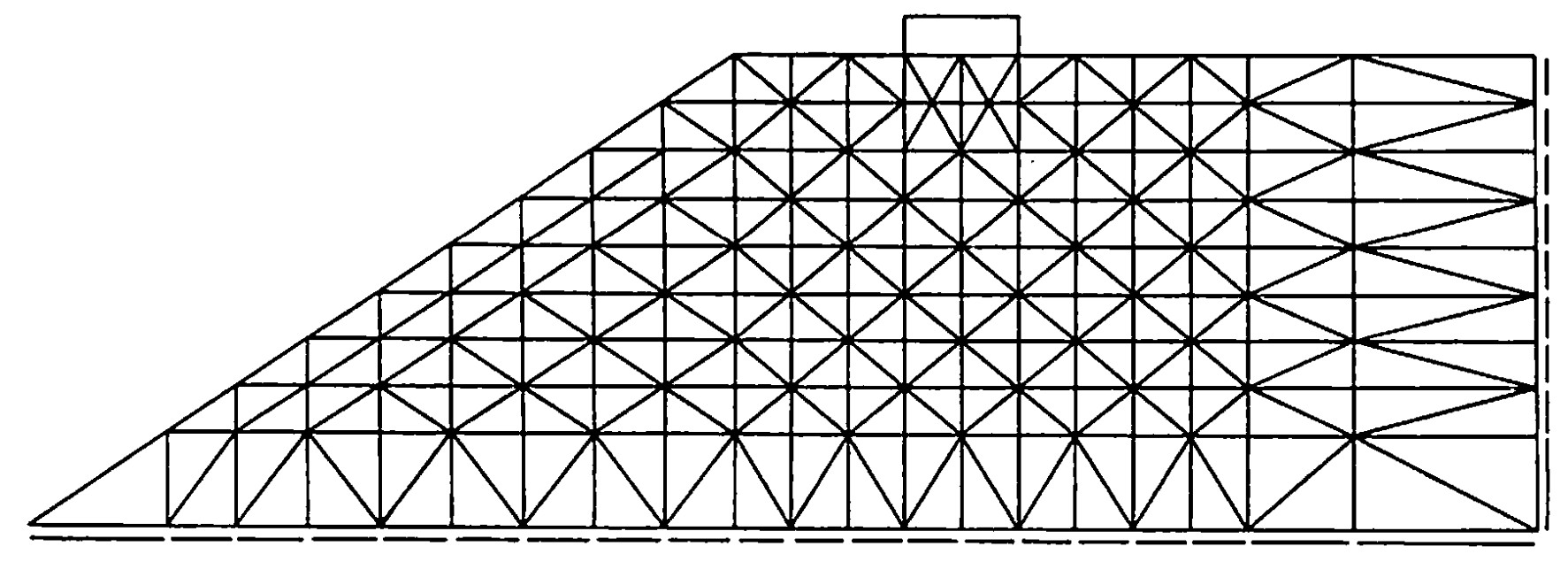
$\hspace{10em}$図4.26 要素分割図
図4.27は実験によるすべり線と円弧すべり解析による安全率を示したものである。この実験のように層すべりが発生する場合、円弧すべり面による近似は難しい。一方、
図4.28は川井モデルによるすべり線で、実験による層すべり破壊とほぽ同一の破壊パターンが得られている。
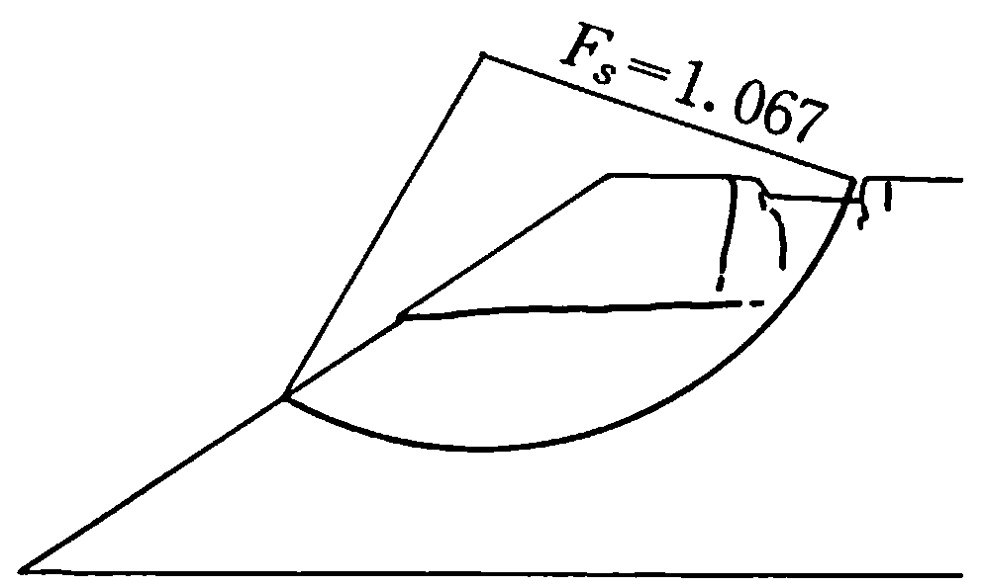
$\hspace{4em}$図4.27 円弧すべり計算結果
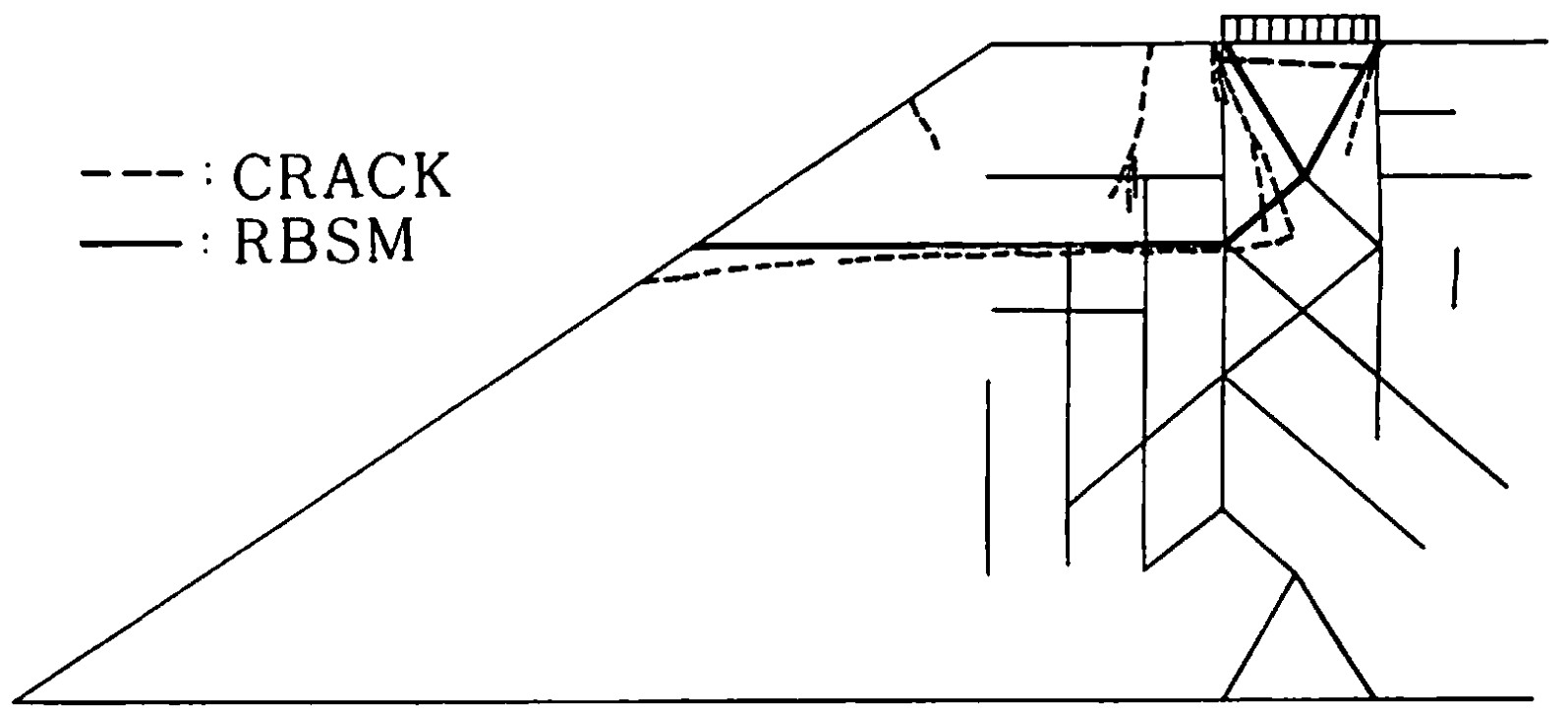
$\hspace{3em}$図4.28 RBSMによるすべり線パターン
図4.29は荷重一沈下曲線を比較したもので、割線弾性係数を用いて計算しているため、若千柔らかめの挙動を示している。極限支持力は川井モデルによる場合、$3.611 {\rm kgf/cm^2}$、実験値が $3.11 {\rm kgf/cm^2}$ であり、約16%の誤差であった。
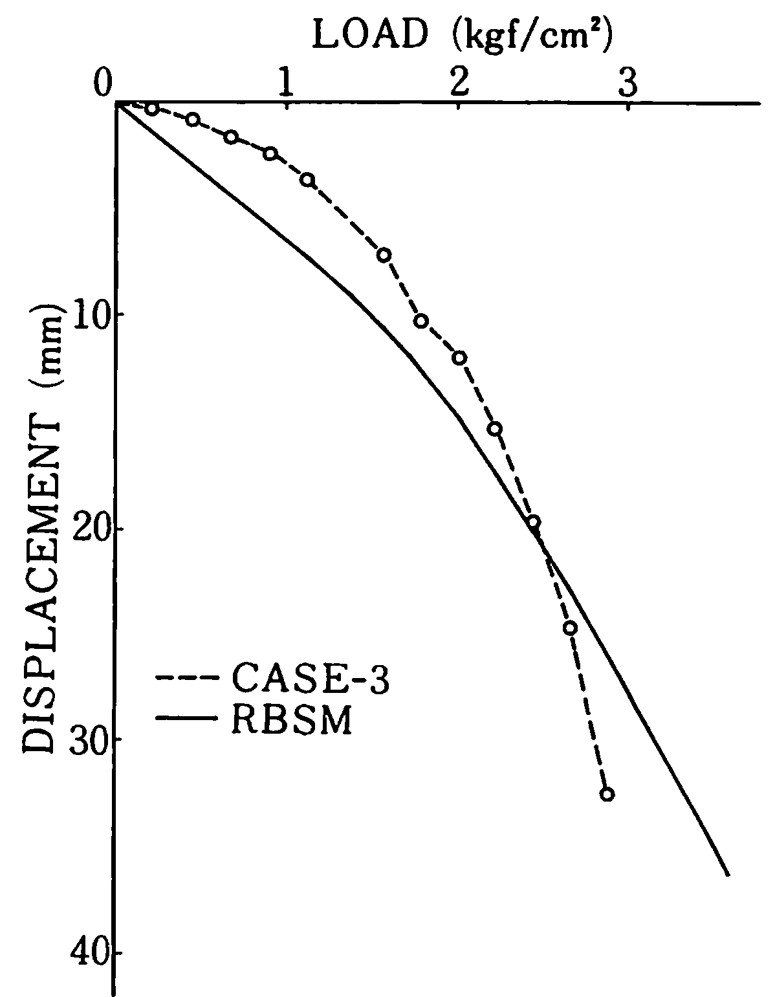
$\hspace{4em}$図4.29 荷重-沈下曲線
また、載荷重に対するN0.8点の土圧の変化状況を比較した結果が
図4.30に示されている。
図4.31 はNo.13に着目し、横軸に載荷重を、また、縦軸に垂直変位をとりプロットした結果である。荷重レベルに応じて垂直変位が増加する傾向かよく現れている。
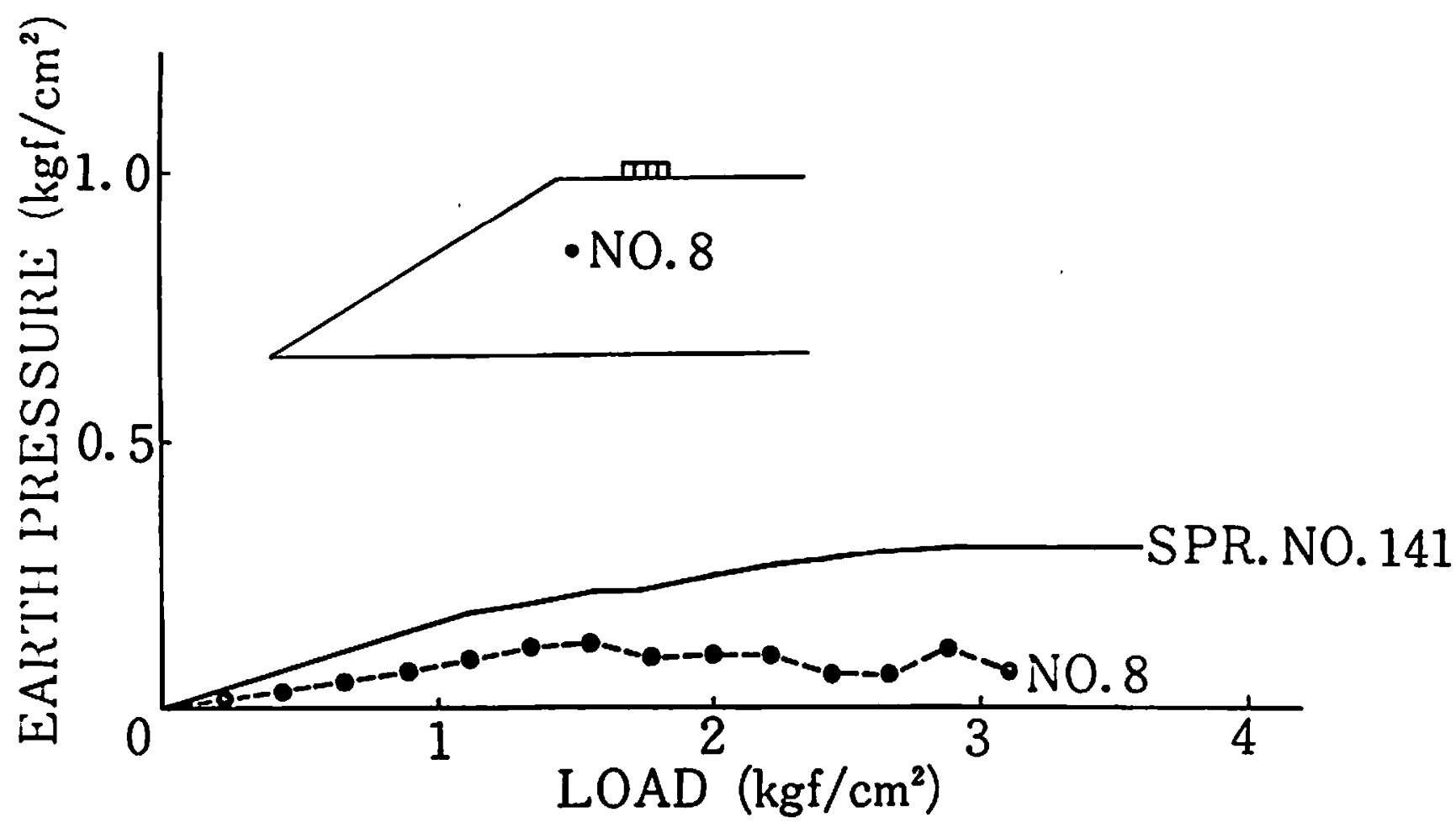
$\hspace{5em}$図4.30 斜面内部の土圧
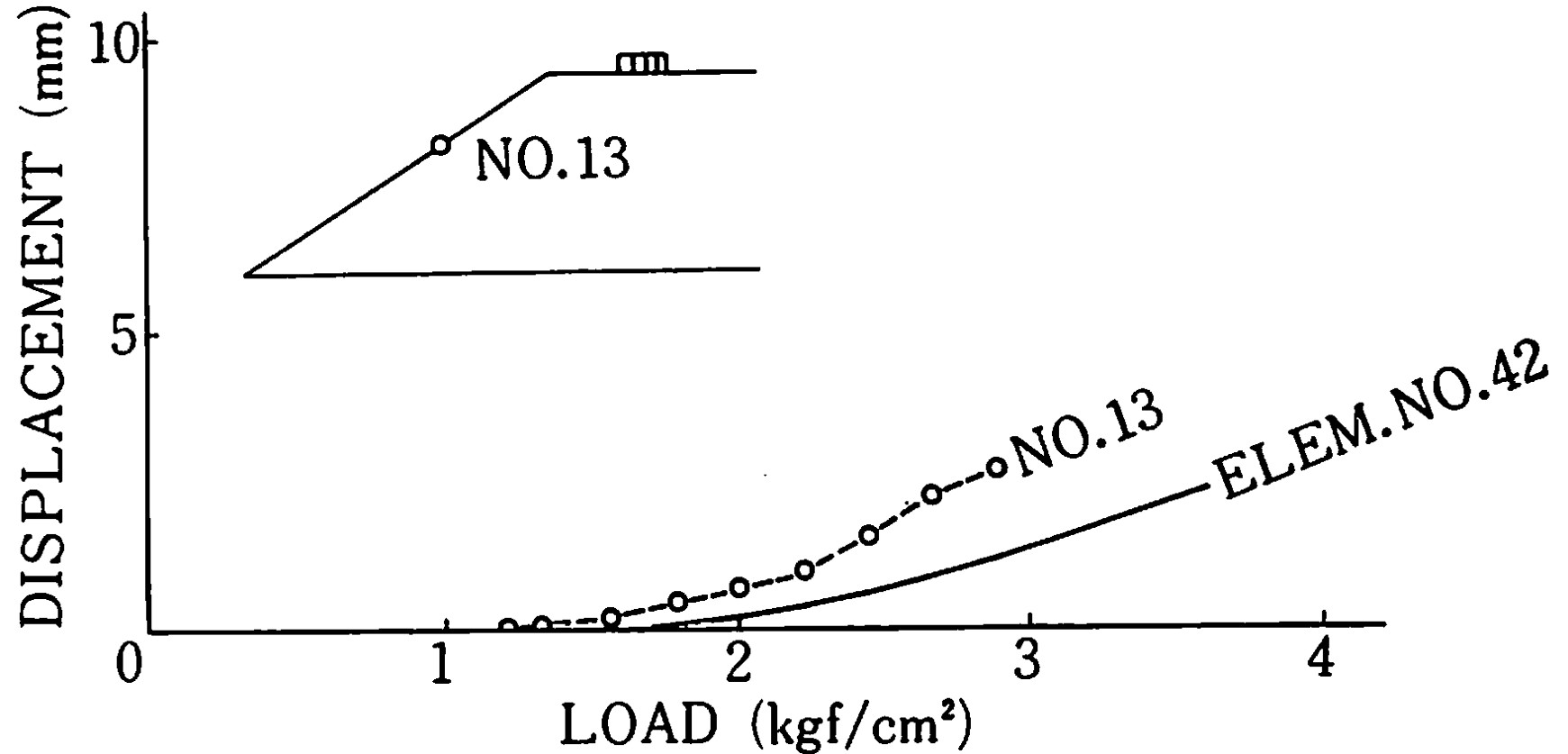
$\hspace{5em}$図4.31 斜面上の垂直変位































