斜面は自然に存在するもの以外に盛土や切土などによって人工的にも形成される。この斜面は、例えば、ダムであるとか河川の堤防、宅地造成地などのように重要な構造が多く、事故時の被害の大きさを考えると慎重に安定性を検討しておく必要がある。
斜面安定問題の解析には斜面の幾何学形状、土性状態などを考慮しながら斜面をスライスに分割し、分割細片での力の釣合を考える分割法が多く用いられており、安全率という概念を導入して斜面の危険度を判定している。この分割法は2次元解析が主体であったが、計算機の利用により、近年では3次元分割法も試みられるようになってきた。また、信頼性解析を取り入れた分割法も提案されている。
一方、有限要素法を利用した解析も数多く試みられ、一応の成果を上げている。Araiらは下解定理を利用した有限要素法による極限解析を提案している。ただし、これらの方法では明確なすべり線を得るのが難しく、また、要素分割などのデータ作成に手間がかかるなどの問題点もあるため、設計に直接利用するには若千の問題があるようである。
本節では、川井モデルをこのような斜面安定問題に適用する方法について説明する。以下に解析上の注意事項について整理する。
(1)解析領域と境界条件
斜面安定解析を有限要素法や川井モデルなどのような領域型解析法を用いて行う場合、最も注意を要する点の1つとして解析領域の決定がある。支持力問題の場合、基礎周辺を中心にし、前章で示した考え方により領域を決定すれば比較的良好な解を得ることができるが、斜面安定解析の場合は明確な領域決定法はない。自然に存在するような斜面の場合、解析領域としてかなり広い範囲を設定しなければ良い解が得られないことも度々ある。このような場合、過去の計算結果を参考にするのも一つの方法である。
図5.1は川井モデルを用いた離散化極限解析を行う場合の左右の境界設定例である。
図(a)では斜面の法面傾斜が最もきつい箇所と左端の境界が交差している。このような場合、境界からすべり面が発生する可能性が高いため、あまり好ましい領域設定とはいえない。また、右端も傾斜の途中で法面と境界が交差しているため、すべり面が境界に達する可能性かある。傾斜角度や地質状況を検討し、すべりが発生する可能性がある場合には、このような境界の設定も避けるべきであろう。できるだけ、
図(b)のように領域を設定した方が良い解を得ることができる。
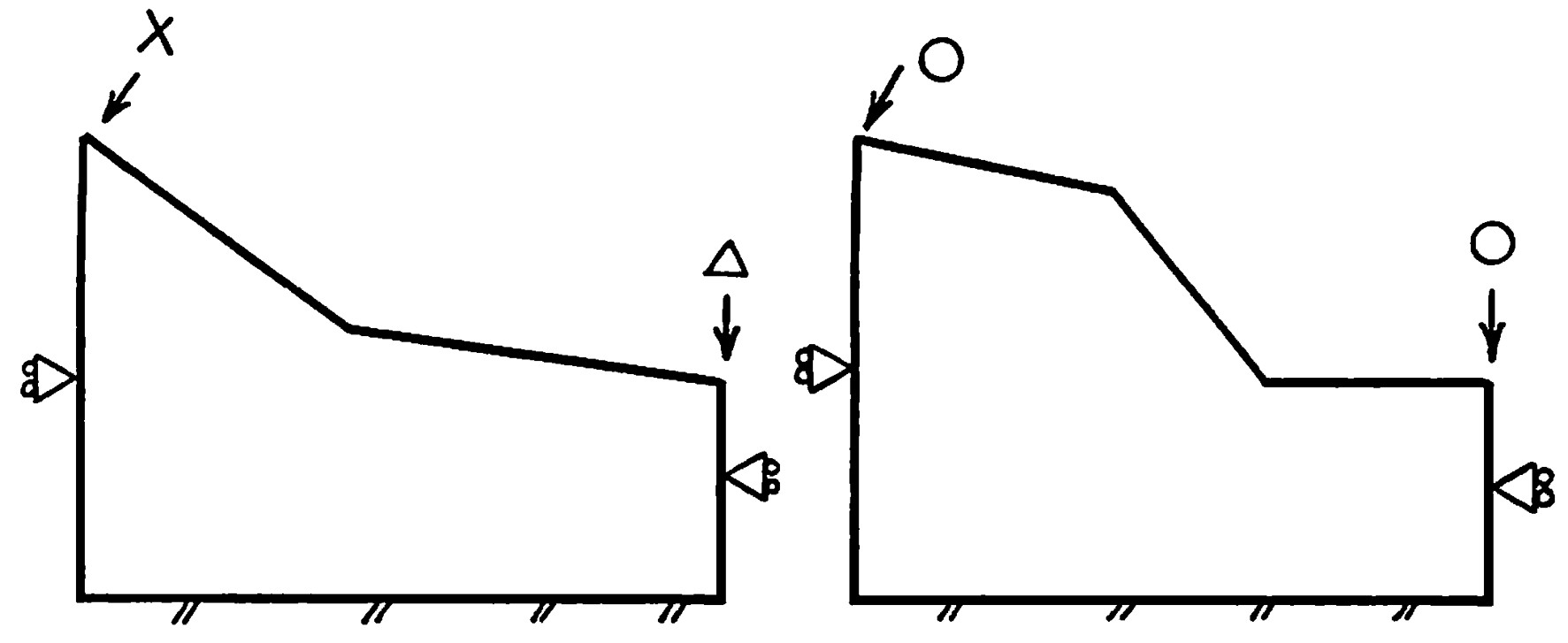
$\hspace{3em}$(a)悪い領域
$\hspace{6em}$(b)良い領域
$\hspace{8em}$図5.1 左右の境界
一方、底部の境界については、比較的ゆるい土質の場合、支持層と見なせる程度の十分な強度を持つ深さまで考慮する必要がある。また、岩盤斜面などの場合には強度の高い新鮮岩の位置まで領域に取り込んだ方がよい。
図5.2は新鮮岩の上に風化岩がある場合で、このような場合には図右のように解析領域を考える方法の他、簡便的に図左のように風化岩の部分を取り出して解析することもよく行う。安定解析に着目するなら、このような方法も要素分割が少なくてすみ有効である。ただし、解析を行った結果、重要なすぺり面が境界に達するようであれば、再度領域を見直す必要がある。
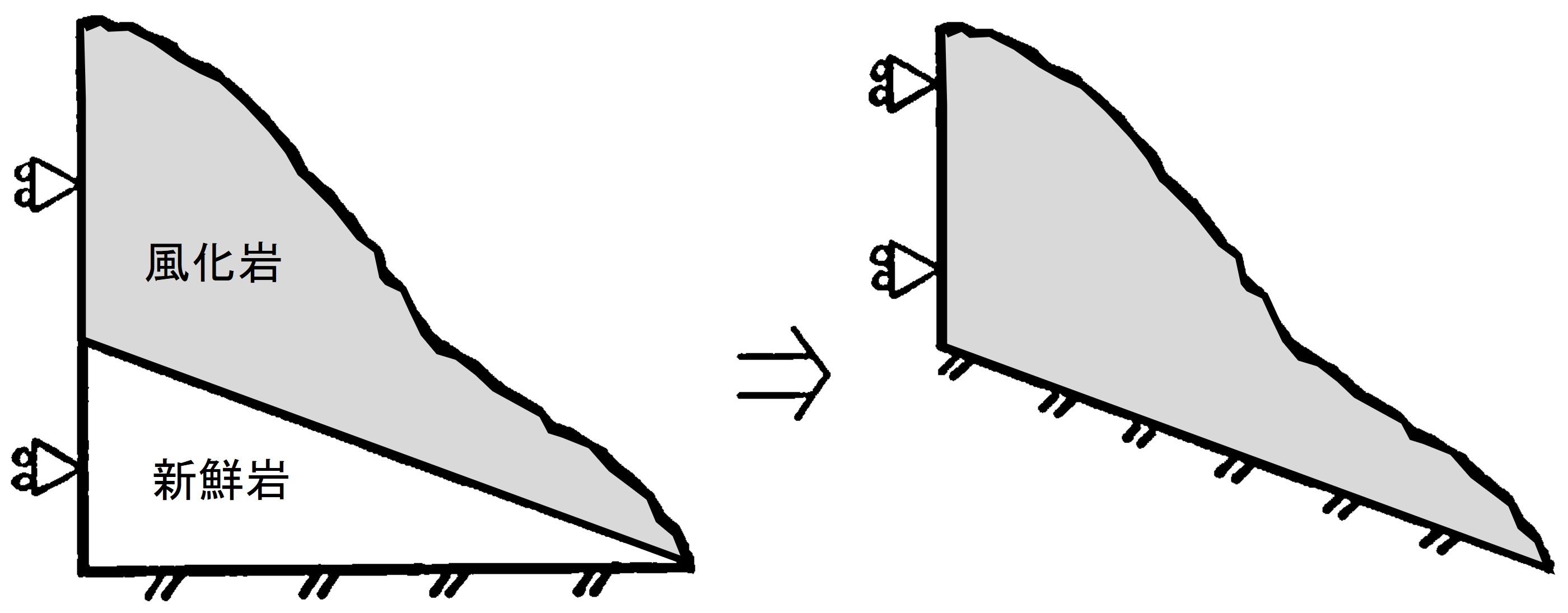
$\hspace{5em}$図5.2 岩盤斜面の解析領域
境界条件については、有限要素法と同様、左右の境界をスライド、底面を固定とすることがよく行われている。
(2)要素分割
要素分割に対する基本的な考え方は有限要素法と同様、極端に偏平な形状にならないこと、また、隣接する要素の大きさが極端に異ならないよう注意を払う必要がある。
要素分割に取り込むべき想定すべり面の考え方は前章の支持力問題とは異なる。一般的に、自然に存在する斜面の場合、内部の地層状況や法面形状、初期地圧などが複雑であるため、理論的にすべり面を決定することは難しい。
地盤が均質で、あまり節理、層理が含まれないような斜面、例えば、盛土斜面のような場合には対数ら線を利用する方法も考えられるが、
図5.3(a)に示すよう、簡便的に円弧すべり面を幾つか考え、それらを含むような形式で要素分割を行うとよい。
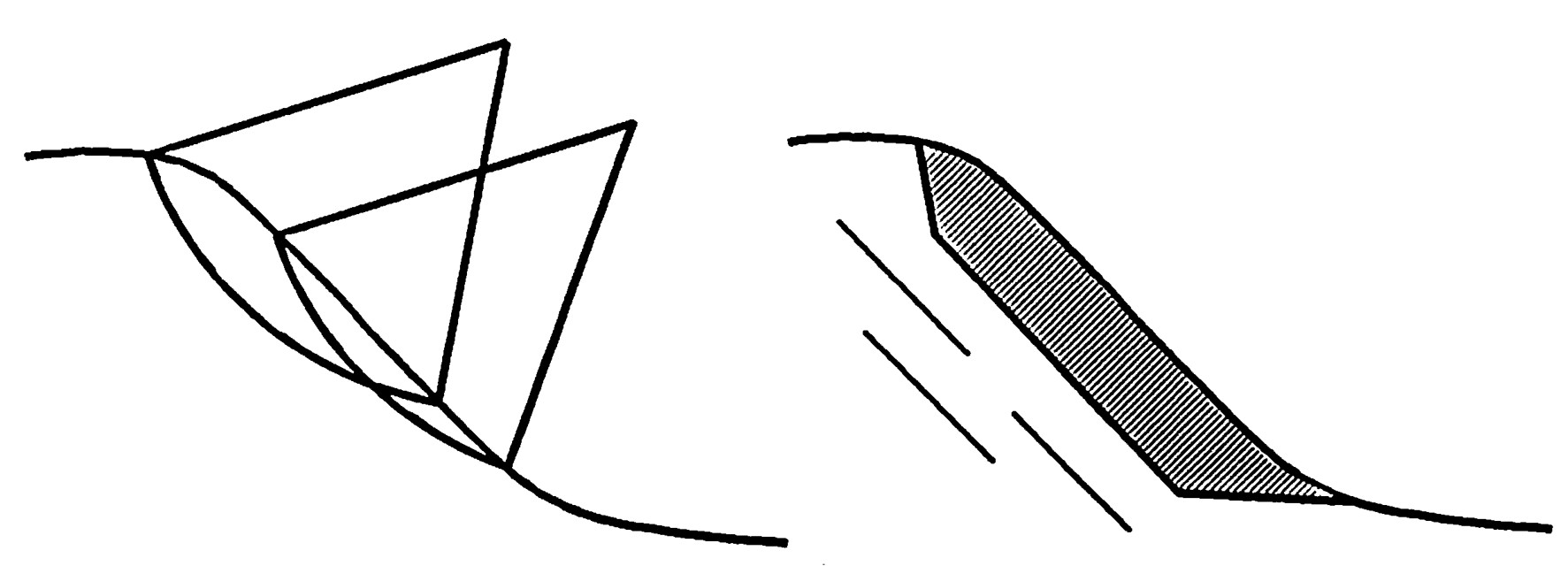
$\hspace{4em}$(a)円弧すべり面$\hspace{4em}$(b)層すべり面
$\hspace{8em}$図5.3 想定すべり面
一方、岩盤斜面などのように節理や層理を多数含む場合は、
図(b)に示すよう、節理、層理に沿って要素分割を行えば、構造的な異方性を解析に考慮することができる。また、岩盤斜面の場合、風化の度合いが少ないほど要素分割を大きくすることにより、より現実的な解が得られる場合が多い。
図5.4は要素分割例を示したもので、
図(a)が比較的粗めの分割、
図(b)が細かめの分割を行った場合を示したものである。
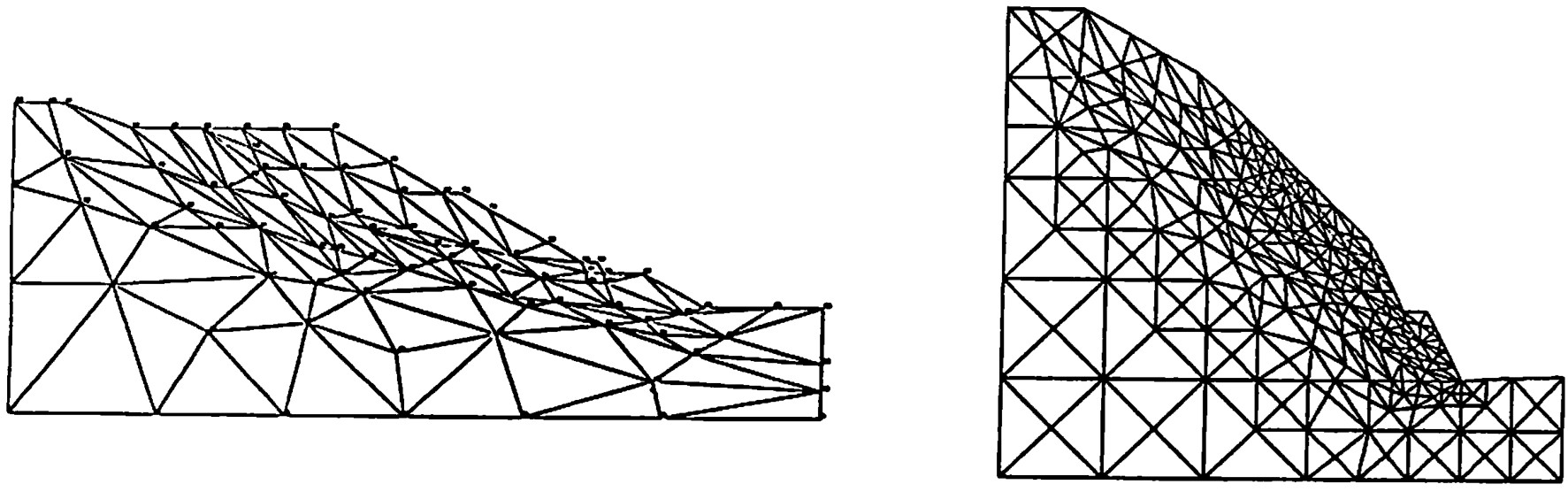
$\hspace{6em}$(a)粗めの分割
$\hspace{9em}$(b)細かめの分割
$\hspace{15em}$図5.4 要素分割例
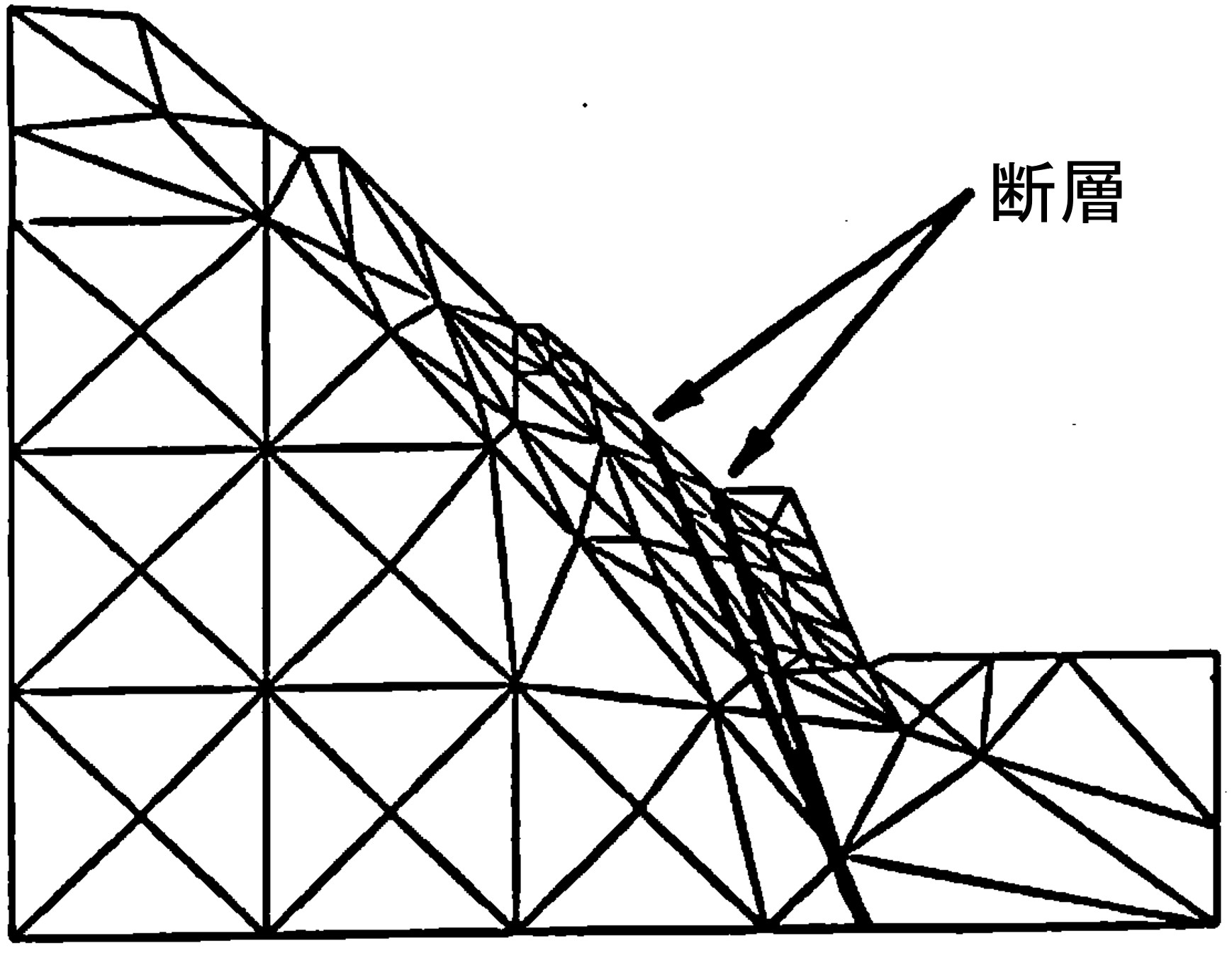
斜面内に断層などが含まれる場合には
図5.5に示すように要素分割へ考慮することで、有限要素法においてよく利用されているジョイント要素などの特別な要素を挿入せずにすむ。ただし、断層部分に該等する要素境界上のばねについては
図5.6に示すよう、断層の材料定数を指定する必要がある。
$\hspace{0em}$図5.5 断層を含む斜面の要素分割例
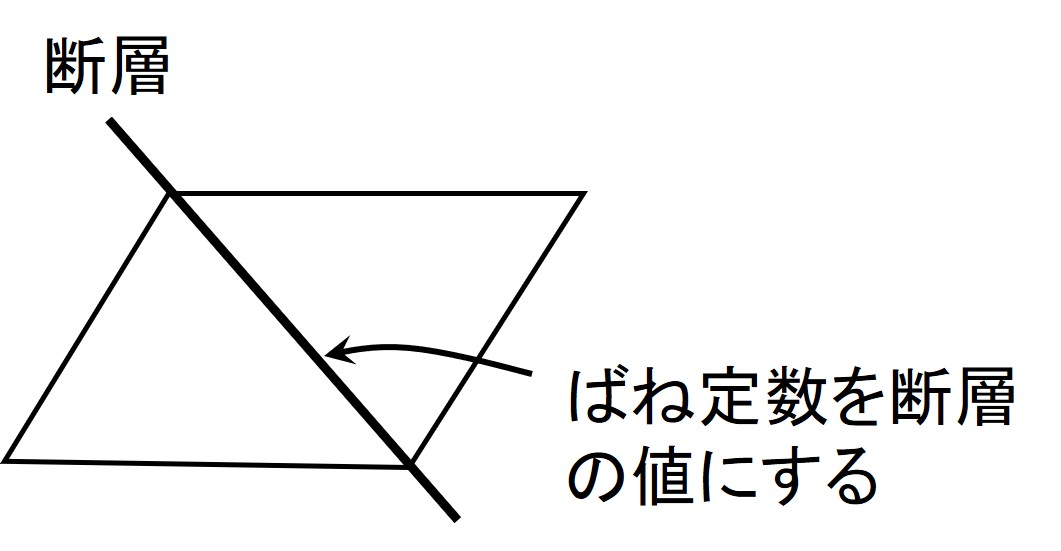
$\hspace{4em}$図5.6 断層のばね
(3)解析ステップ
初期地圧の決定は解析結果を左右するほど重要な課題であるにもかかわらず、特別な方法はない。便宜上、自重により計算から求める場合、計算結果のうち、応力のみを採用し、変位は無視することがよく行われている。盛土計算の場合、
図5.7に示すよう予め自重による初期地圧を計算し、変位をクアした後、盛土材の自重を載荷重として計算する。
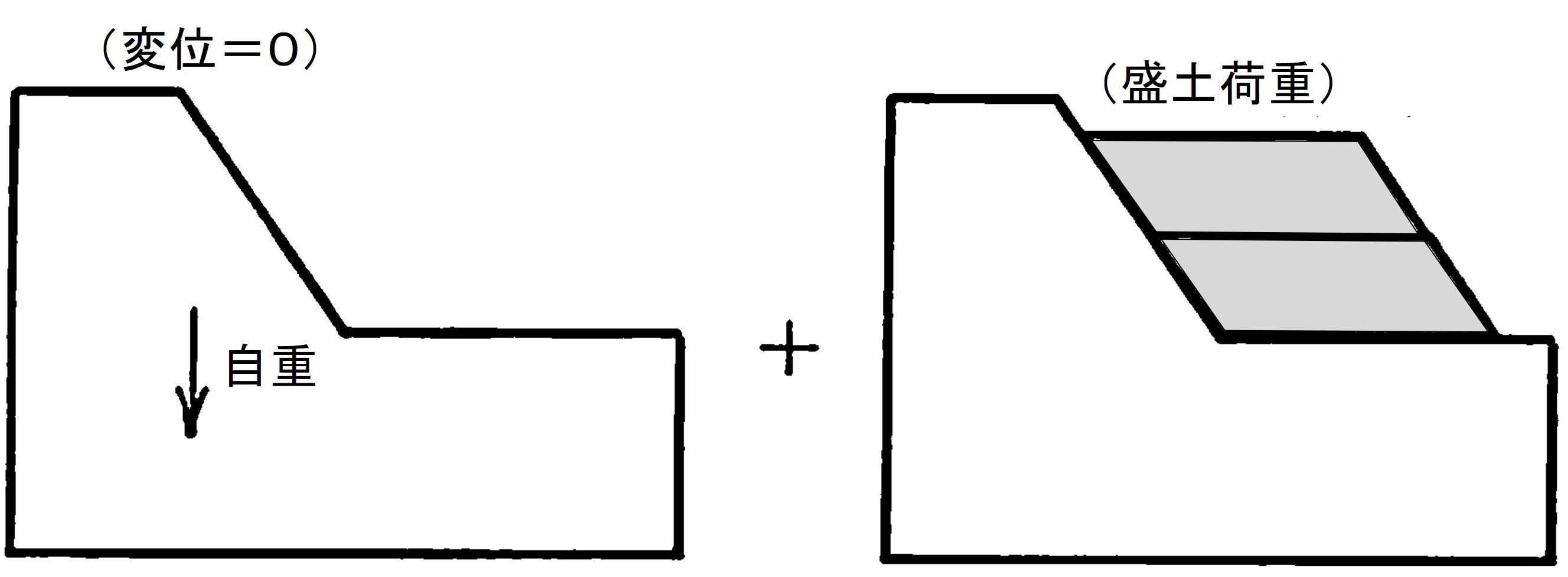
$\hspace{2em}$(a)初期地圧計算$\hspace{8em}$(b)盛土
$\hspace{9em}$図5.7 盛土計算
切士の場合は
図5.8に示すよう、掘削相当外力により計算を行う。しかし、簡便的に切土後の斜面形状をもとに自重による安定解析を行う方法がよく行われている。なお、掘削相当外力の求め方については次章において説明する。
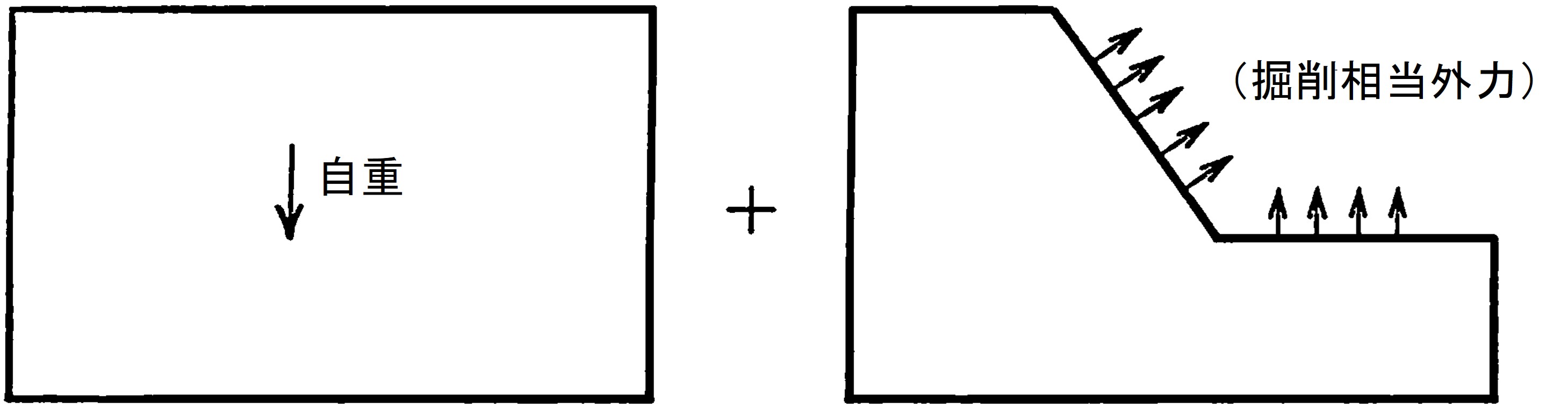
$\hspace{2em}$(a)初期地圧計算$\hspace{6em}$(b)切土
$\hspace{8em}$図5.8 切土計算
(4)安全率
地盤の安定性を評価する場合、安全率という概念が一般的によく利用されている。この安全率を破壊プロセスに応じて定義すると以下のように分類できる。
現在の土質力学では、これらのうち、強度安全率が広く用いられている。斜面安定問題においても極限平衡法を基礎とする解析法がよく利用され、円弧を代表とする仮定すべり面上のせん断強度に対する安全率が議論されている。
これと同様な考え方を有限要素解析やRBSMによる離散化極限解析を行った結果に適用する場合、想定すべり面上の安全率を以下のように求めることができる。
\[{\rm (5.1)}
F_s = \frac{\sum ( C + \tan \phi) \cdot l}{\sum \tau \cdot l}
\]
このようにして求めた斜面全体の安全率は、極限平衡法により求めた値より、一般的に高めの値を示す傾向にある。
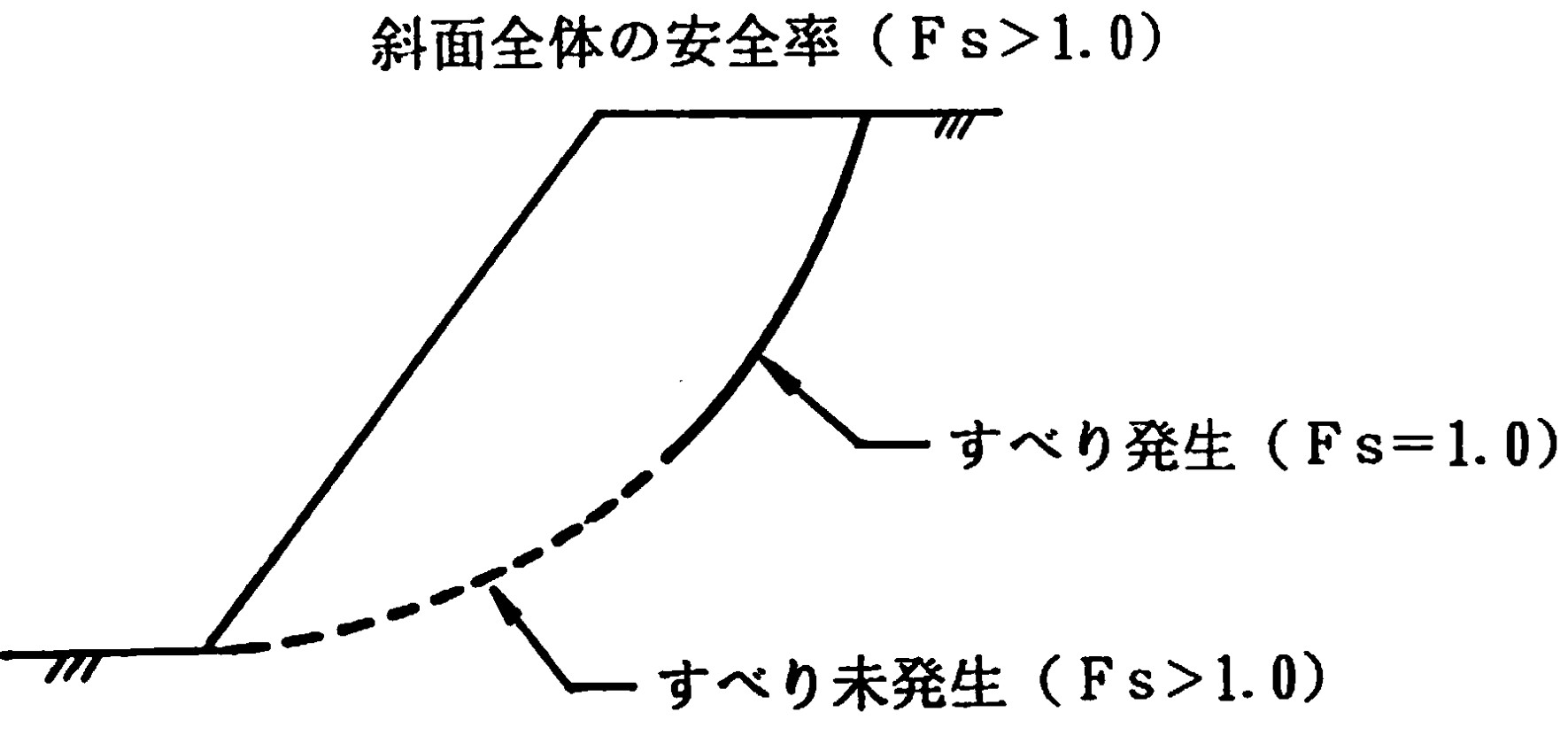
図5.9は川井モデルによる想定すべり面上の安全率を示したもので、すべりが発生している箇所では安全率 $F_s=1.0$ となり、未発生の部分では必ず1.0より大きくなる。
$\hspace{4em}$図5.9 想定すべり面上の安全率
この関係は斜面全体の安全率が1.0より大きい場合、すなわち、斜面が崩壊しない場合のもので、もし、斜面が崩壊する場合には
式(5.1)の関係を利用して安全率を求めてもすべり面上では $F_s=1.0$ となり意味がない。このような場合には、荷重増分法における山田の方法を用いて自重戟荷率(荷重増分率)という意味の重量安全率を考えるとよい。これは、単位体積重董の何%が作用し時点で斜面が崩壊するかという考え方であり、斜面が崩壊する場合の安全率は $F_s=r_{\rm min}(荷重増分率)\lt 1.0$ なる関係となる。
(5)非線形解析法
斜面の初期地圧を計算により求めるような場合には反復法を利用することができるが、安定解析が中心となる場合には、山田の方法による荷重増分法が適している。この理由としては、斜面崩壊が発生するような湯合、反復法では解が収束しないこと、崩壊状況が把握できないことなどがある。急斜面などで引っI張りクラックが発生する恐れがある場合には、すべり破壊のみを対象とする安定解析ではなく、
3.5節で説明した引っ張り破壊を考慮した山田の方法を用いた方がよい。
始めに、川井モデルの特性を理解するため、底部破壊をすると思われる簡単な均一斜面を取り上げ安定解析を行う。一般に、内部摩擦角を $0^{\circ}$ とした場合、斜面の傾度と深さから破壊形式を知る図表がTaylorによって与えられている。ここでは、これを参考にして
図5.10に示すような斜面を考え、半径 $R$ を変えることにより、安全率がどのように変化するか調べてみる。半径 $R$ は図に示すよう、$16、20、25、30 \; {\rm (m)}$ の4通りとした。要素分割ならびに境界条件については図に示す通りである。
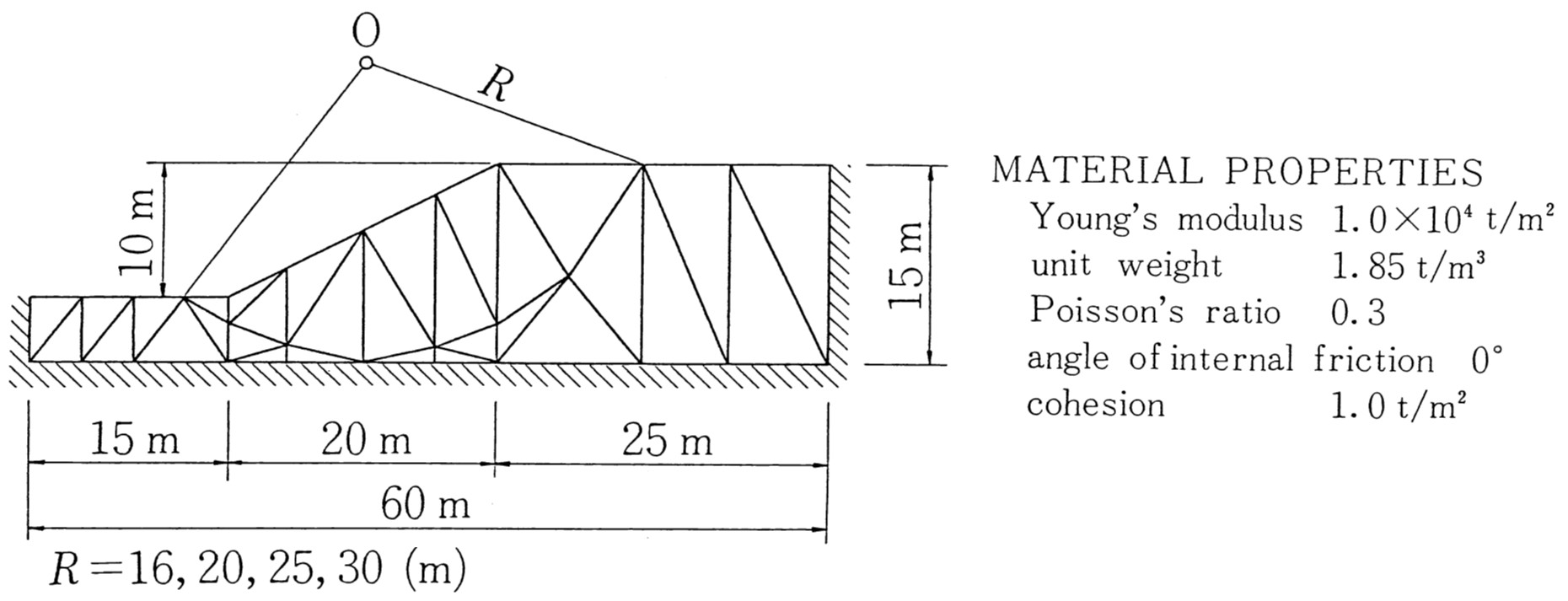
$\hspace{10em}$図5.10 均一有限斜面のモデル
図5.11には $R$ を変えて離散化極限解析を行った結果が示されている。すべり線についてはどのケースについても同じ傾向が見られる。計算によれば、仮定した円弧面にすべりが発生したとき、斜面は破壊機構を形成し崩壊する。ただし、境界条件として底面を固定しているため、斜面先端部の底面にもすべり線が発生している。
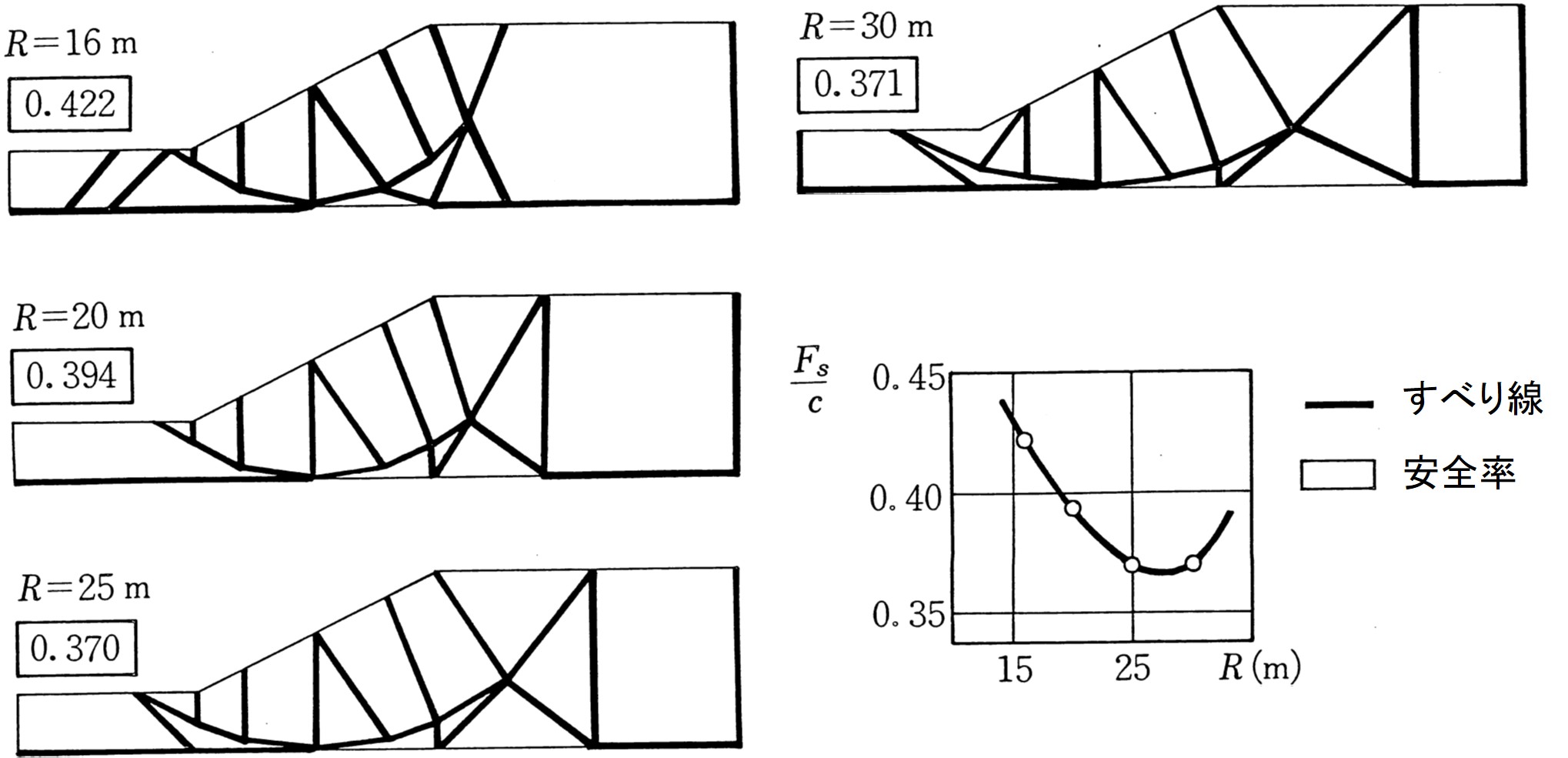
$\hspace{8em}$図5.11 $R$ の変化によるすべり線と安全率
次ぎに、安全率について考えてみよう。ここでは、
5.1節で述べたように安全率を自重載荷率より求めている。すなわち、斜面が崩壊したときの単位体積重量 $(\gamma')$ と本来の土の単位体積重蓋 $(\gamma)$ の比 $(\gamma' / \gamma)$ を重量安全率として考えている。図は各半径を横軸にとり、安全率を縦軸にとっている。この図より、約 $27.5{\rm m}$前後で最も安全率が低くなることが予想される。
そこで、
図5.12に示されるように、半径が $20、27.5、35 \; {\rm m}$ の円弧が含まれる極端な要素分割を行い、どのすべり線が卓越するか解析した。すべり線の状況は $27.5 {\rm m}$ の円弧より小さい円弧では斜面前方が破壊しやすく、逆に大きな半径の円弧では後方がすべりやすいという結果となっている。最も危険であると予想された $27.5 {\rm m}$ の円弧では全面にわたりすべり線が発生し、このすべり線によって斜面は崩壊する。このときの安全率は、先の安全率からも推測できるように0.366という値であった。
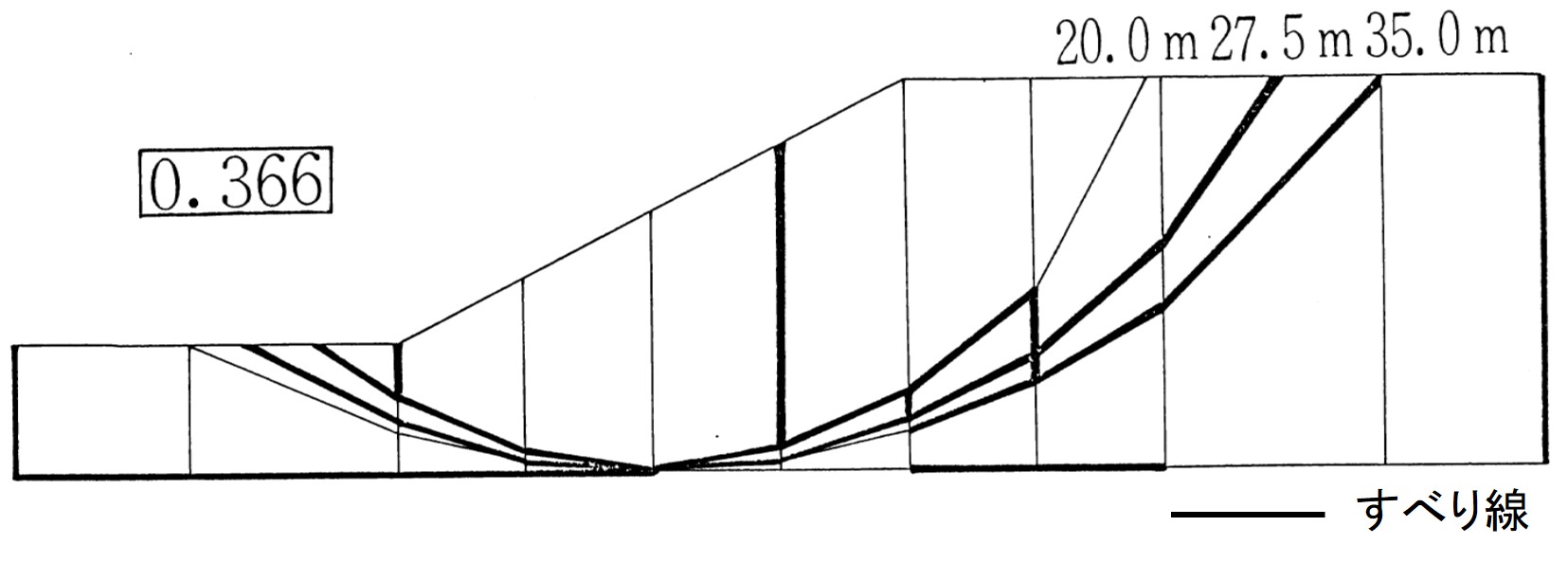
$\hspace{4em}$図5.12 様々の $R$ を含む計算結果
このように、川井モデルによる離散化極限解析では与えられた要素分割の中から最良のすべり線パターンを自動的に計算する。この考え方を利用し、さらに簡略化した斜面安定解析法については
5.5節において説明する。
ここでは斜面安定問題の応用例として地すべり問題の解析例を示す。本例は長野県信州新町で発生した奈良尾地すべりをモデル化したものである。地すべりは比較的ゆるやかな勾配の斜面で発生し、その破壊形態は単純な円弧で表現することができず、複雑な複合すべり面を形成することが多い。したがって、通常の円弧すべり解析では明確なすべり線を限定することができず、最も危険なすべり面を探すのには不適切な場合が多い。
地すべりの発生において間隙水圧の影響は多大なものであると考えられるが、実際の地下水の分布状況を知ることは困難なことであり、特に降雨後の一時的な非定常の状態を解析的に求めることは極めて難しい。また、仮に地下水の分布状況が把握できたとしてもすべり面に作用する水圧を地下水位から換算する方法は必ずしも正しい間隙水圧を示すとは限らない。
地盤の応力解析において利用される強度定数は土質系地盤の場合、三軸試験結果を利用することが多い。完全に飽和した粘性土の場合、この試験法のうち非圧密非排水試験結果を利用し、$\phi=0$ 法により解析することがよく行われている。斜面内部に発生する間隙水圧を正しく評価できない限り有効応力表示を用いてもあまり意味がないため、ここでは、便宜上、ある一定の地盤が地下水により飽和状態になったと仮定し、その地層の内部摩擦角が働かなくなったとして解析を試みた。
図5.13に解析に用いたモデル図と材料定数か示されている。材料定数表の中に計算を行ったケース番号が記載されている。ケース1は実際に地すべりが発生した付近の地層が地下水により飽和状態になったと仮定し、その部分の内部摩擦角を0とした例である。ケース2はさらに飽和領域が地表面近くまで増えたと仮定したもので,ケース3は完全に地表面まで飽和したと例である。
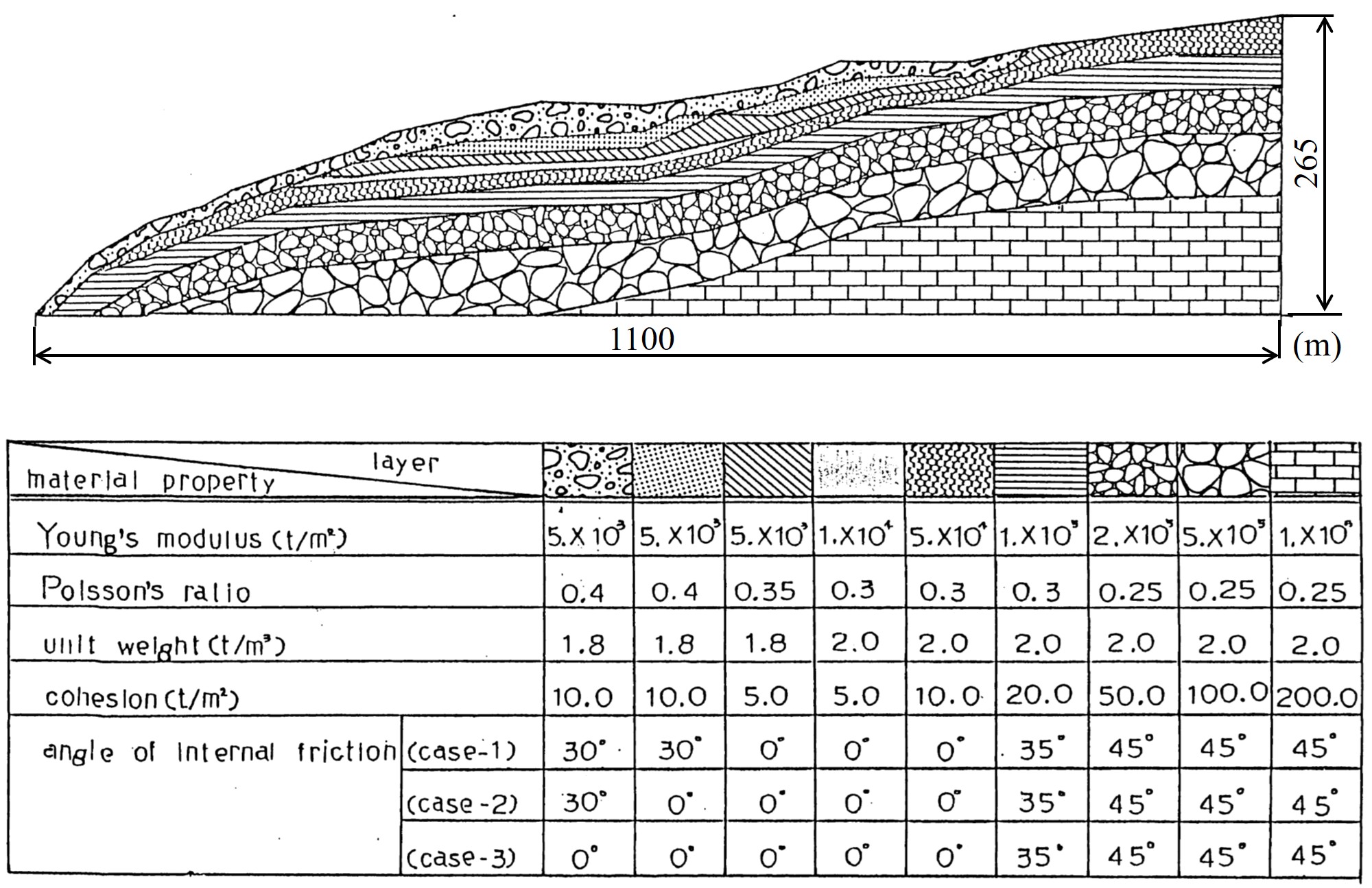
$\hspace{10em}$図5.13 解析に用いたモデルを材料定数
図5.14は計算に用いた要素分割が示されている。境界条件は底辺を固定、側辺を上下方向自由とした。また、非線形解析法については自重を荷重とする山田の方法を用いている。
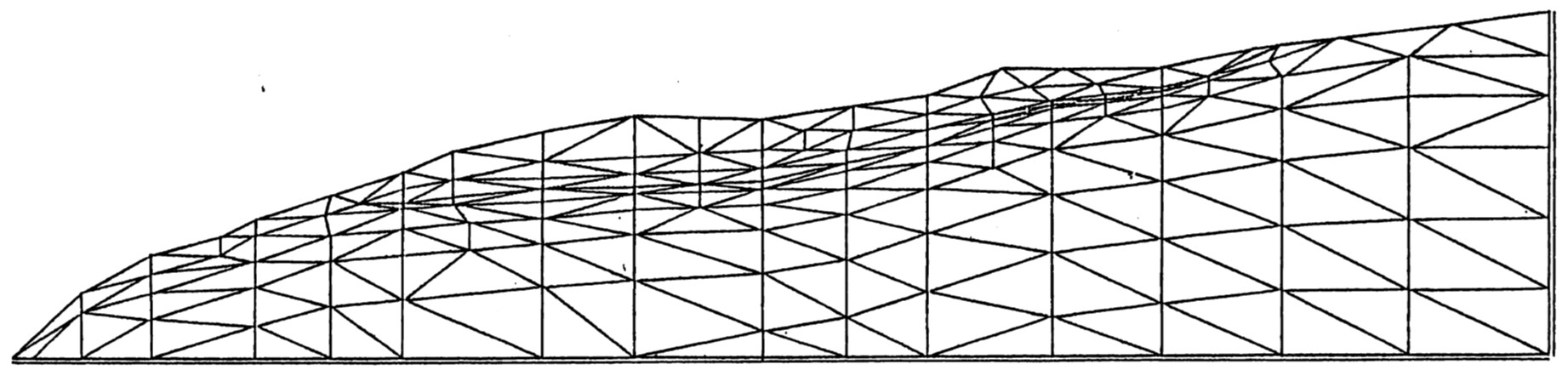
$\hspace{10em}$図5.14 要素分割図
図5.15は計算によるすべり線発生状況を示した図である。黒塗りの部分が地下水により飽和状態になったと仮定した部分で、実線がRBSMにより得られたすべり線、破線が現実に発生した地すべり面を表している。ただし、表現の都合上、縦軸のスケールを半分にしている。それぞれの計算ケースを眺めてみると、飽和領域の仮定の相違にもかかわらず、一定のすべり面によって斜面が崩壊している。このことからただちに結論を出すことはできないが、地山の形状や地層構造に間隙水圧によって影響を受けやすい箇所があり、それが何らかの間隙水圧の上昇に伴い地すべりが発生したものと思われる。
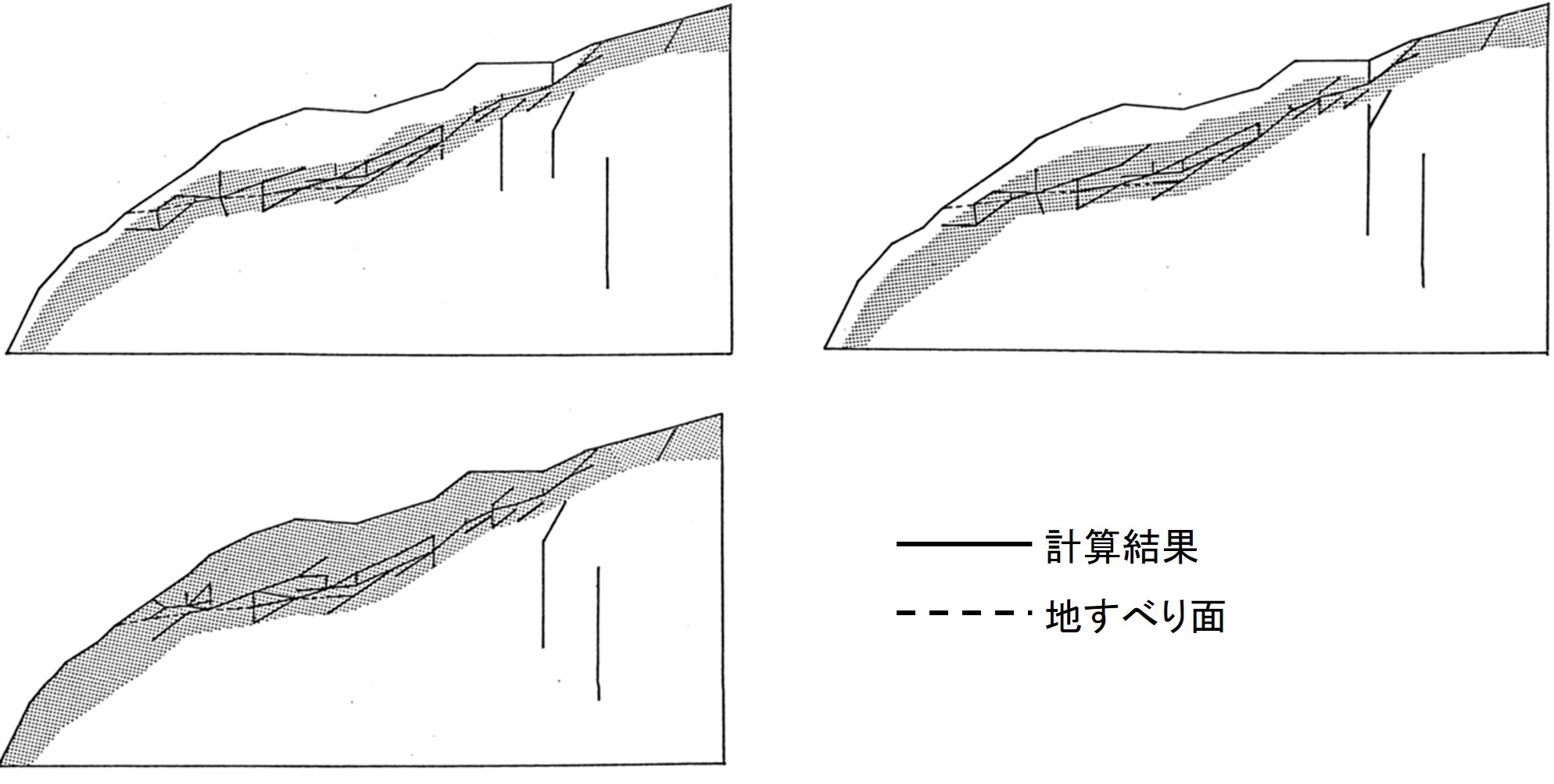
$\hspace{10em}$図5.15 地すべり面と計算結果
ここで示した例とは異なるが、もし、斜面が完全に水没しているような場合には、簡便的に浮力を考慮して解析する方法も考えられる。しかし、本質的に浸透流解析による結果との連成を考慮することも必要であろう。
斜面の安全性を確保するため、施工現場では各種の法面保護工法が採用されている。
図5.16は代表的な工法を示した図である。
図(a)の切土工は、切土法面を1:1~2程度の緩勾配に再カットすることで安全性を確保する工法である。また、
図(b)のアンカーエはアンカーボルトにより斜面を押さえ付ける工法で、
図(c)のロックボルトエは短いロックボルトを多数打ち込み、斜面構造をブロック化することで強度を上げる工法である。ここでは、このような法面保護工法のうち、アンカーエとロックボルト工を取り上げ説明する。
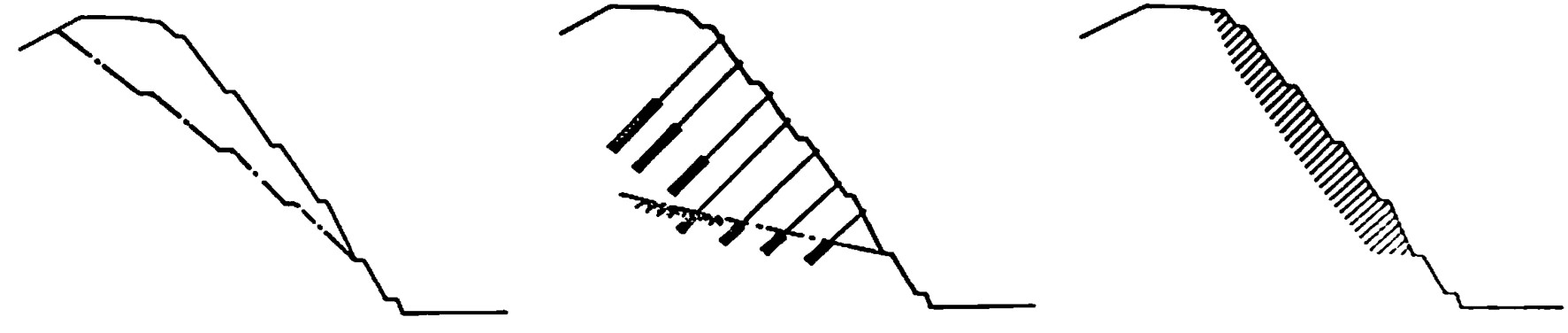
$\hspace{2em}$(a) 切土工
$\hspace{5em}$(b) アンカー工
$\hspace{3em}$(c) ロックボルト工
$\hspace{11em}$図5.16 各種の法面対策工
図5.17はアンカーエに対する数値解析上のモデル化の方法を簡単に示した図である。
図(a)はアンカーとして梁要素を用いる方法で、有限要素法による解析でもよく利用されている。

$\hspace{4em}$(a) 梁要素
$\hspace{6em}$(b) 荷重
$\hspace{5em}$図5.17 アンカー工のモデル化
川井モデルにより離散化極限解析を行う場合においても、
- (1)梁要素は軸力のみ作用するトラス要素とし、曲げモーメントは受けない
- (2)アンカーの定着部以外は地盤に関する平面要素と結合しない
などの注意事項は有限要素法解析の場合と同じである。このように、アンカーを梁要素に置換し、平面ひずみ状態で解析する場合、アンカーに緊張力を与えると定着部の挙動が実際の挙動と異なることも多いため、取り扱いは慎重にしなければならない。
一方、
図(b)はアンカーの緊張力を等価な外力に換算し、簡便的に解析を行う方法である。この方法は要素分割に際しアンカー位置をあまり気にせずに済み、概略検討に多用されている。ここでは、
図(b)の方法を用いた場合の解析例を示す。
図5.18に解析に用いたモデル図を示す。破線の部分がもとの地形で、実線が掘削後の地形である。解析は平面ひずみ状態を仮定し、破壊規準としてモール・クーロンの直線包絡線を用いている。また、非線形解析法としていは荷重増分法における山田の方法を採用した。一般に、アンカーカが設計上決まっていて、そのアンカーカで斜面が安定であるか検討する場合は反復法による解析も有効である。
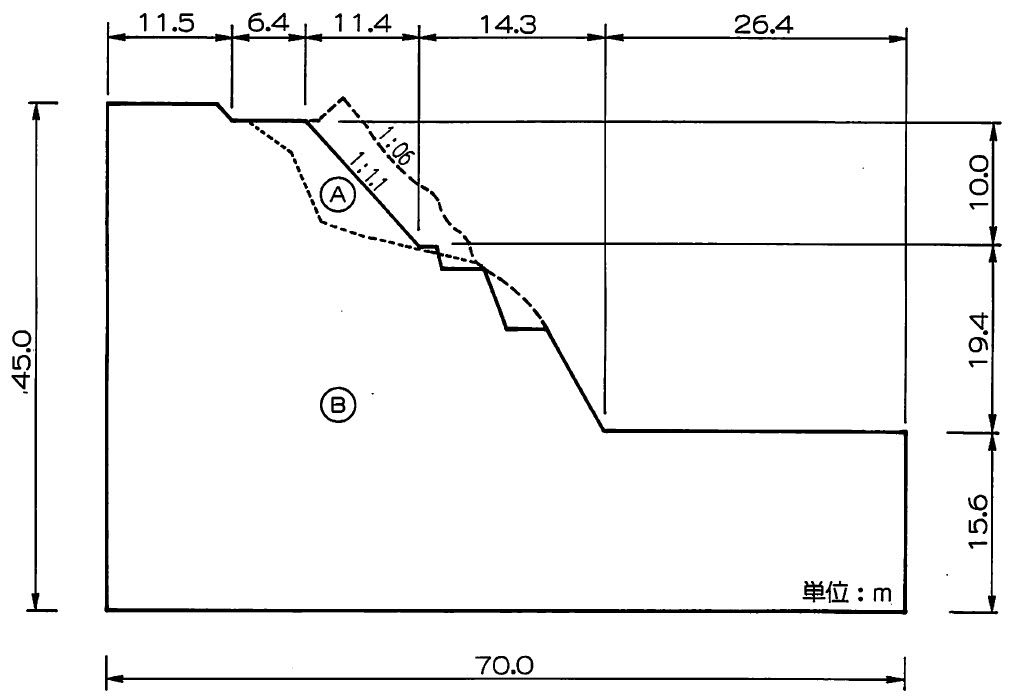
$\hspace{10em}$図5.18 岩盤斜面のモデル
表5.1は計算に使用した物性値が示されている。この物性値の決定はボーリング・データーより行うのが最も一般的であるが、解析上、地盤を構造体としてとらえたときのマクロ的な物性値については、円弧すべり法などを利用して逆算し、見かけの物性値として採用することも度々ある。この点については次ぎの例題において説明する。
表5.1 計算に用いた材料定数
| 材料定数 |
単位 |
A |
B |
| 弾性係数 |
${\rm P_a}$ |
$4.9 \times 10^7$ |
$4.9 \times 10^7$ |
| ポアソン比 |
- |
$0.3$ |
$0.2$ |
| 単位体積重量 |
${\rm kN/m^3}$ |
$17.7$ |
$25.5$ |
| せん断強さ |
${\rm P_a}$ |
$7.85 \times 10^3$ |
$7.85 \times 10^5$ |
| 内部摩擦角 |
${\rm DEG}$ |
$36$ |
$45$ |
斜面切り取り時の計算結果を
図5.19に示す。この図を眺めると、斜面を切り取ったときの計算によるすべり線はメカニズムを形成しており、実際の斜面が崩壊する危険性は極めて高いと考えられる。また、円弧すべり法による計算結果も川井モデルによる計算結果と類似しており、安全率も0.99で崩壊の可能性を示している。
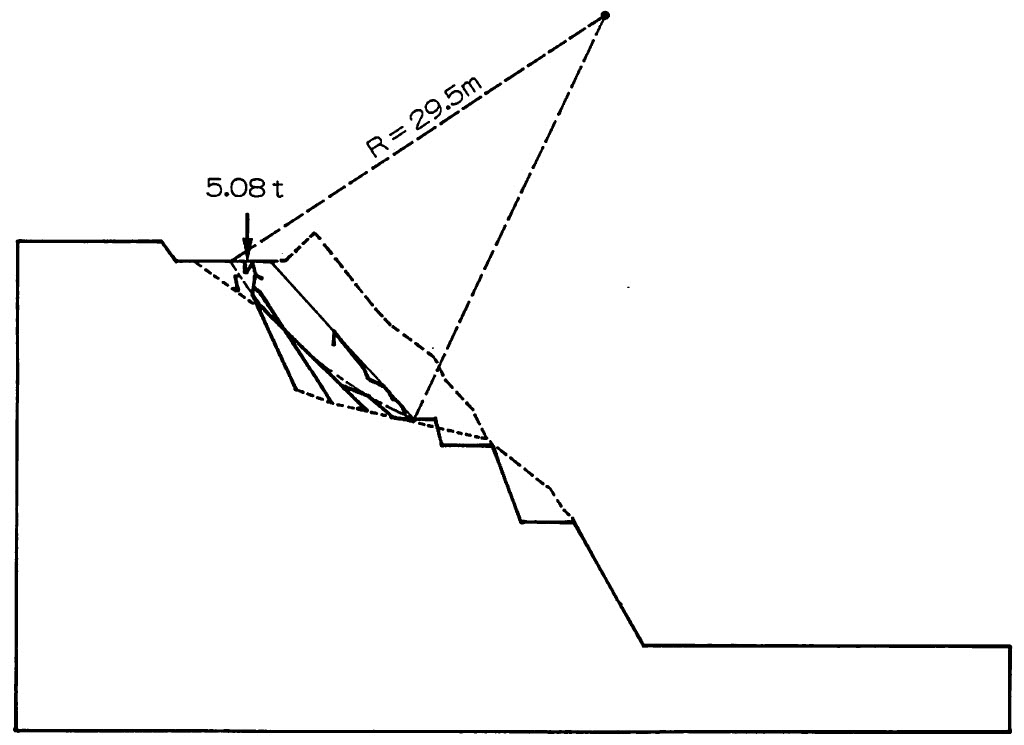
$\hspace{4em}$図5.19 斜面切り取り時の解析結果
次に、斜面安定の補助工法として、アースアンカーを考慮した場合の計算結果を
図5.20に示す。アース・アンカーカは図に示すよう、等分布荷重として考慮した。図の結果はアンカーカが $15 {\rm t}$ の場合である。アンカーカが増せば、すべり線は地山の奥に移動し、また、発生箇所も減少する。図からも理解できるように、アンカーカが $15 {\rm t}$ の場合、斜面は比較的安全であると考えられる。
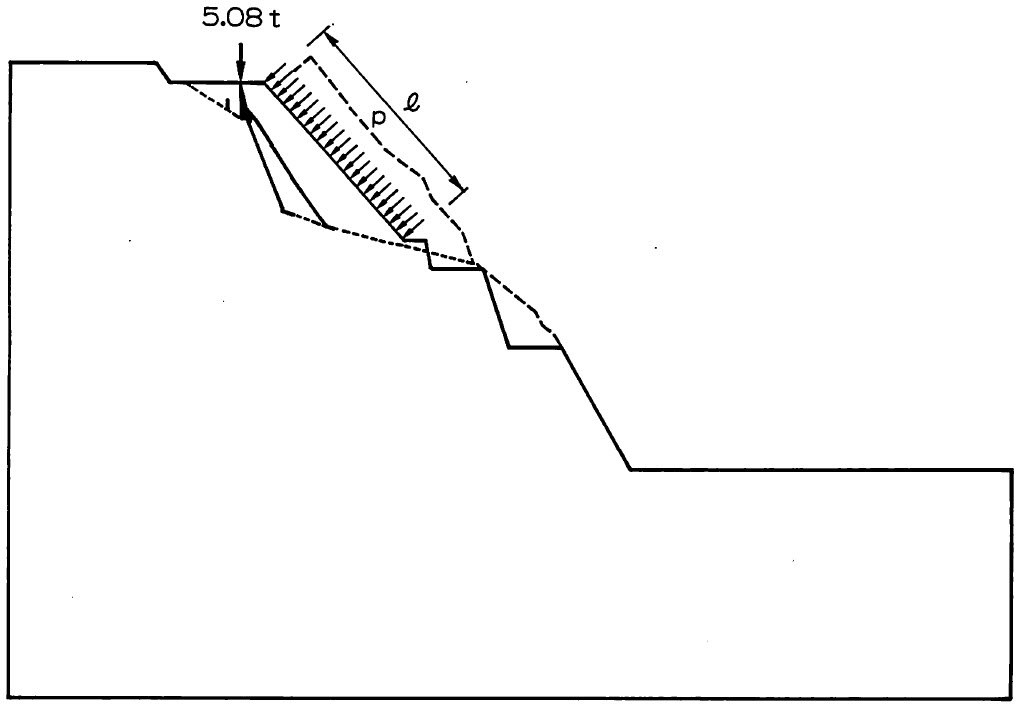
$\hspace{4em}$図5.20 アンカー力を考慮した解析結果
斜面が永久構造物であるための安全率 $F_s$ を1.2とし、この安全率を得るために必要なアンカーカ $P$ を土質工学会「アースアンカー設計施工基準」にしたかって計算してみる。計算に当たり、円弧すべり計算により求めたすべり線をモデル化し、安全率 $F_s$ を以下の式により求める。
\[{\rm (5.2)}
F_{S} = \frac{MR+(P \cos \beta + P \sin \mu )R}{MO}
\]
これより、奥行き1m当たりのアンカーカ $P$ は、$\cos \beta$ を安全側として無視することで
\[{\rm (5.3)}
P = \frac{MO \cdot F_{S} - MR}{R \sin \beta \cdot \mu}
= 14.57t
\]
となり、先の川井モデルによる結果と比較すると、妥当な値であろう。
次ぎにロックボルトエ法の例を取り上げてみよう。
図5.21は節理系の地盤をモデル化したものである。風化の進んだ堆積岩では図のような層理、節理が発達し、層理面に沿ってプロック状に割れる場合が多い。このような地盤では切土に伴い法面が乾湿の繰り返しで風化が進み、節理・クラックなどの脆弱部のせん断強度が低下し滑落が生じている場合も多々ある。また、滑落した層理面は鏡状を呈することもあり、この場合はせん断抵抗がほとんど得られないこともある。
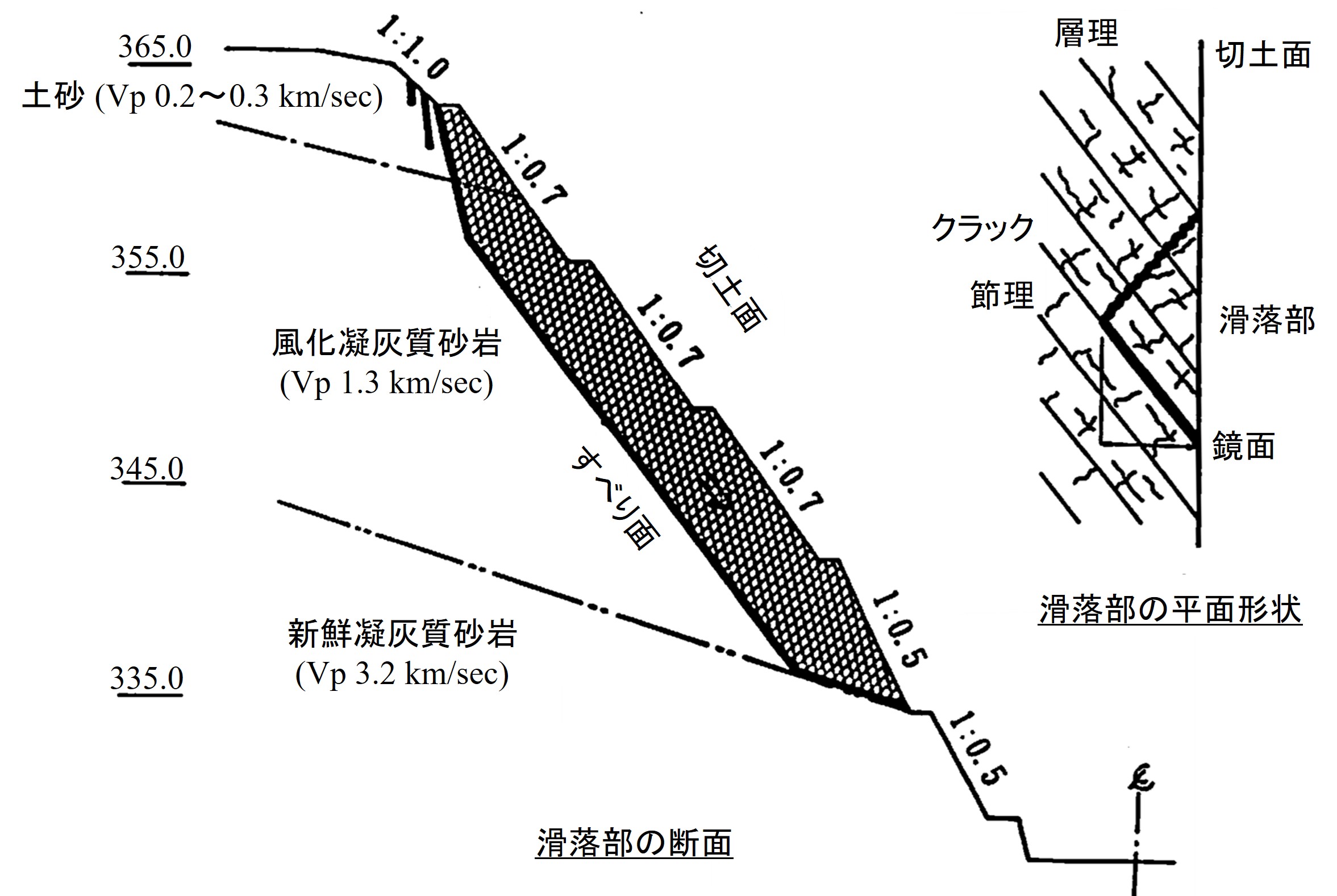
$\hspace{6em}$図5.21 層理・節理系斜面のモデル
解析にあたり、材料定数が詳細に得られていなかったり、節理系の地盤で見かけの強度が予想以上に弱い場合は試し計算を最低でも数回行っておく必要がある。特に、事故時の施工対策などに離散化極限解析を利用するのであれば、滑落の形状を予め調査し、逆解析を行い見かけの材料定数を推定するのもよい。しかし、現在のところ離散化極限解析における数理的な逆解析の方法は確立されておらず、試行錯誤的に行わざるをえない。
ここでは、
図5.22下段に示すよう、材料定数を3ケース仮定した。図上段には滑落前における斜面の離散化極限解析結果が示されている。ケース1ではすべり線が深部に発生し、2段目の法面部が上部荷重によって滑り出す結果になり、調査した滑落の状況と整合しない。ケース2はすべり線が4段目の法面まで達し、斜面は崩壊する。このすべりの深さは実際の滑落状況を再現するもので、仮定した材料定数が比較的合致しているものと思われる。ケース3は地盤内部に不連続なすべり線が発生するものの、地表面までは至らず、滑落は発生しない。このような試し計算から判断して地盤の見かけの強度をケース2の状態に設定する。ここで、注意しなければならないことは、見かけの強度が節理・層理などの影響により弱めの値となる場合が多いことである。解析結果を判断する場合、モデル化による影響が現れているのか、あるいは節理・層理地盤の強度を平均化したためであるかを十分吟味しておかなくてはならない。

$\hspace{10em}$図5.22 掘削前の安定解析結果
以上の準備のもと、
図5.23に示すようにロックボルト工法を用いて斜面を補強した場合の解析結果を次ぎに示す。ロックボルトをモデル化する場合、アンカーの場合と同様、梁要素に置換する方法と、せん断強度を増加させる方法の2通りが考えられる。砂地盤のような場合には、ひずみの効果が影響するため、前者の方法が適しているが、ロックボルトに合わせて要素分割を行わなければならず、本数が多い場合には事実上困難である。ここでは、簡便的に後者の方法により解析した結果を示す。
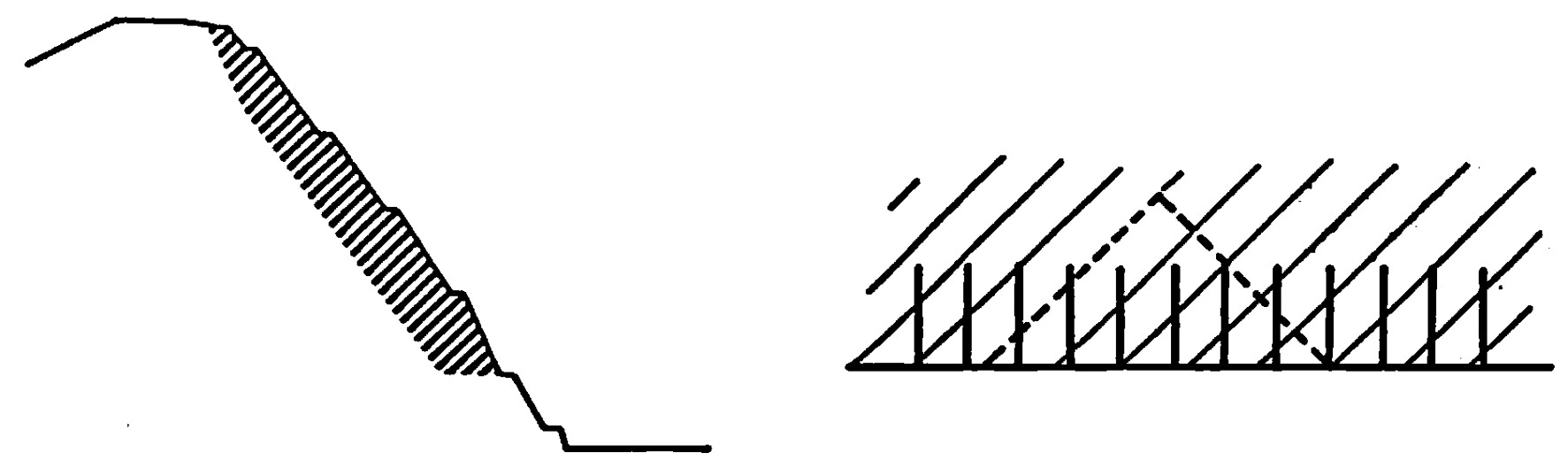
$\hspace{6em}$図5.23 ロックボルト工
図5.24はロックボルトの本数や長さを変えて計算した結果が示されている。上段は長めのロックボルトを少なめに入れた場合の結果で、図右に打設状況、左にすべり線が示されている。この場合、斜面底部に法面を横切るすべりが発生しており斜面崩壊の危険性は高い。中段は短めのロックボルトを数多く打設した場合で、すべりは斜面深部にのみ発生するため、崩壊の危険性を回避することができる。下段は同一長さのロックボルトを斜面位置に応じて本数を変え打設した場合の結果である。中段の結果とほぼ同じであり、経済性の高い打設方法であるといえる。
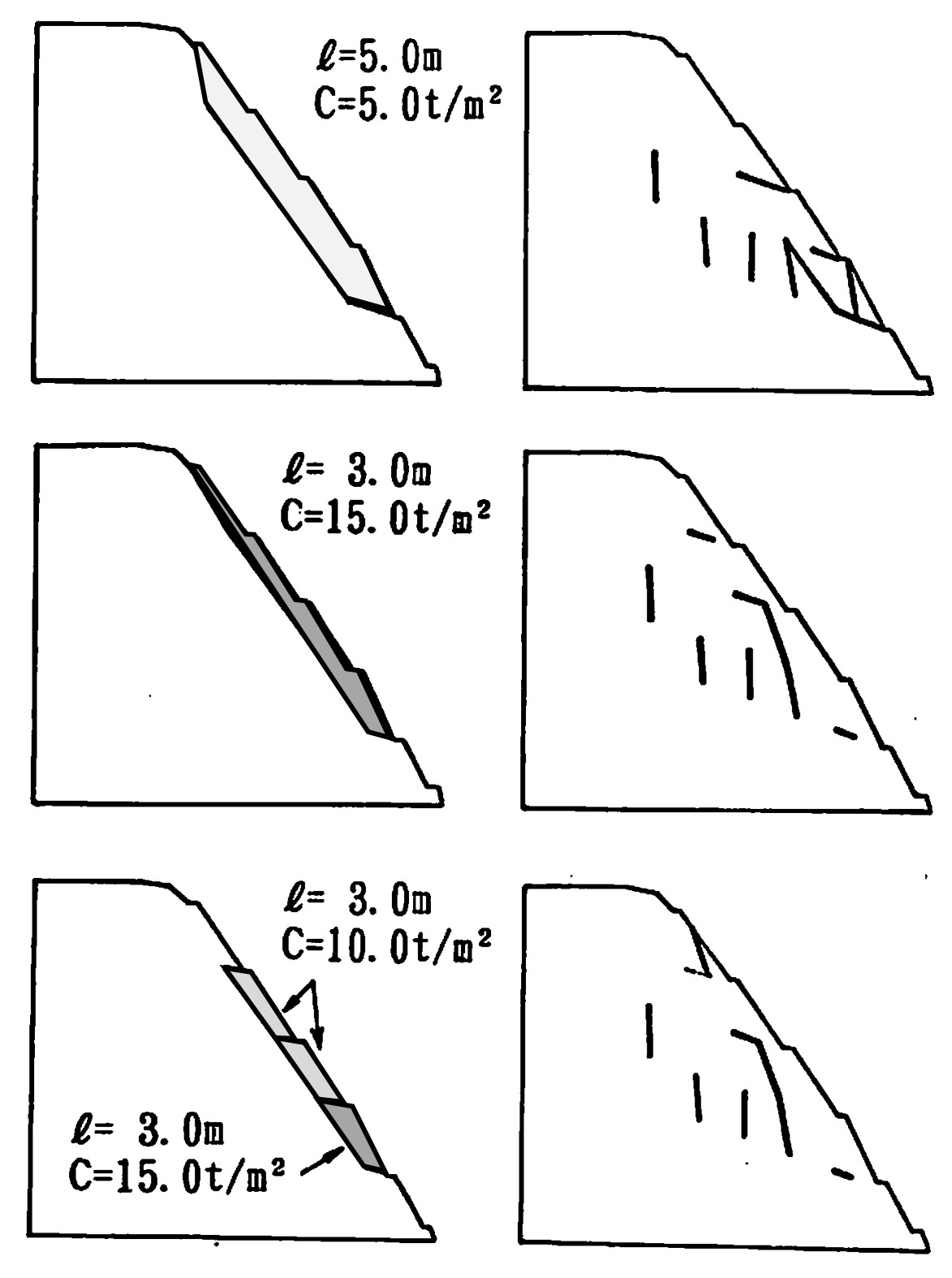
$\hspace{1em}$図5.24 法面保護後の安定解析結果
以上示したように、山田の方法を利用した離散化極限解析では、荷重レベルに応じてすべり線を求めることができるため、各種の施工対策に対して有効に利用できるものと思われる。
斜面安定問題の解析法として分割法がよく利用されている。最も一般的な分割法としては
Sweden法(Felleniuse法)が上げられる。しかし、この方法では 細片分割間の不静定力が無視されているため、
Bishop法や
Spencer法あるいは
Janbu法などのように部分的に不静定力を取り扱う方法が提案されていおり、また、これらをより経済的に解析するための修正法も提案されている。Janbu法と同様、非円弧すべりを取り扱う方法として対数ら線を利用する方法もある。これらの解析法は
極限平衡法を基礎としているため、それぞれの分割細片における局所的な安全率を求め、その値を基に平均化された斜面全体の安全率を算出している。したがって、安全率が1を下回った箇所、すなわち、すべりの発生するであろう箇所においても再配分されるべき力を保持しており、そのような意味では弾性解析的な要素を持った解析法であると考えることができる。
一方、川井モデルはこれまでにも説明してきたように、一般化された極限解析用のモデルであり、与えられた要素分割に対して最良の上界値を与える。このことは要素分割によって上界値が影響を受けることを示しており、要素分割を行う際、十分な注意が必要となる。しかし、常にこのような注意を払いながら計算を行うことは多大な労力を要し、また、計算時間もかかるため、実際の設計においては、従来の方法が若干有利である。
そこで、ここでは川井モデルのこのような性質を逆に利用し、円弧または非円弧をすべり面と仮定した極端なモデル化を行い、すべり面上の塑性仕事だけを評価することで簡便的な川井モデルによる離散化極限解析を行う方法について説明する。この方法では要素分割が一切不要であり、従来の簡便法による解析と同じデーターで解析が可能である。
まず初めに、
図5.25に示すよう、すべり面を円弧に限定した最も簡単な解析法について説明しよう。以下に計算の手順を示す。
- ① 斜面の形状や地層線のデーターを与え、領域内を細片に分割し、これをもとに円弧で囲まれた各々の細片における地盤の重量を計算する。この過程は従来の簡便法と同じである。
- ② 図5.25 に示すよう、円弧の中心と円弧で囲まれた扇型の領域を川井モデルにおける1つの要素と考え、●印間を積分区間、○印を積分点に設定する。すなわち、本解析法では要素は1つということになる。この作業はプログラム内で行うことができ、特別な入カデーターは必要としない。
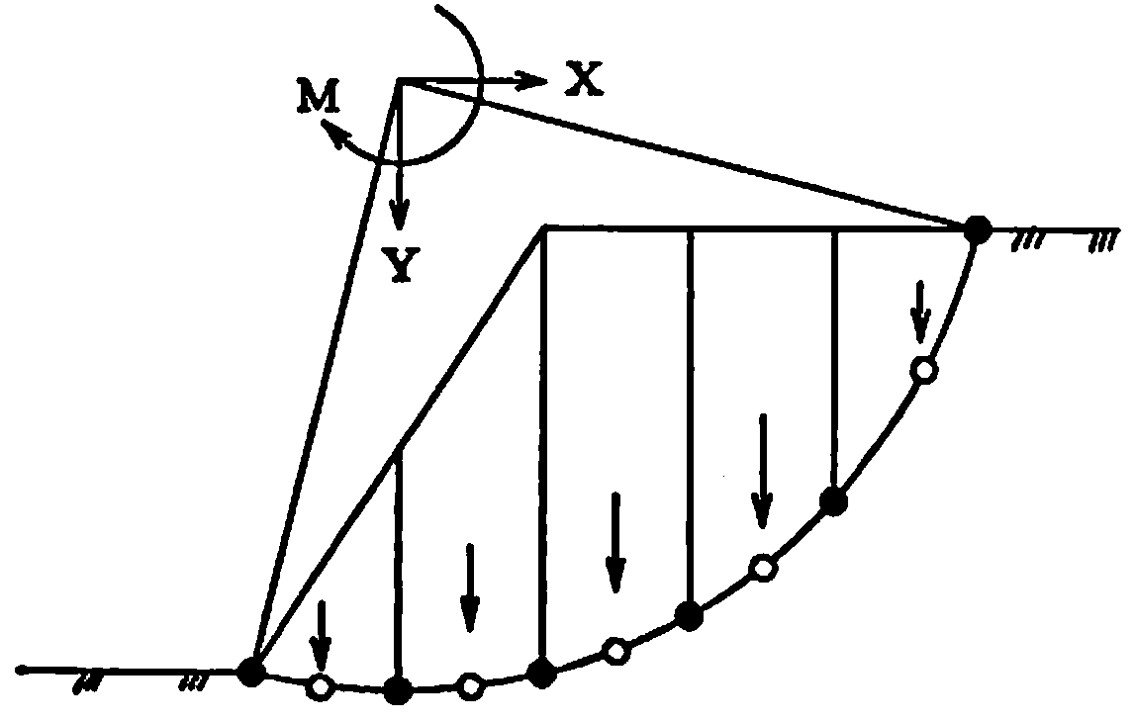
$\hspace{1em}$図5.25 1要素タイプの円弧すべり面と積分点
- ③ 川井モデルの自由度設定位置を円弧の中心にとり、平行変位 $(u, v)$ と剛体回転角 $(\theta)$ の3自由度を設ける。地盤は剛塑性体と仮定し、剛性を無視する。ただし、解析に当たり剛性行列を作る必要があるため、実際には高い剛性をプログラム内部で設定しておく必要がある。
- ④ ①で求めた重量を基に円弧中心における $x、y$ 方向の外力 $(X,Y)$ を計算し、円弧中心と各細片の重量作用位置の距離と重量より円弧中心に作用するモーメント $(M)$ を計算する。
- ⑤ ④で求めた円弧中心の力を外力として川井モデルによる離散化極限解析を行い、各積分点における単位面積当たりの表面力を計算する。
- ⑥ ⑤で得られた表面力から各積分点での安全率を計算し、斜面全体の安全率を以下のように求める。
\[\hspace{2em}{\rm (5.4)}
F_{S} = \frac{\sum ( C + \sigma \tan \phi ) \cdot l}{\sum \tau \cdot l}
\]
このように、本解析法は系全体の自由度が3であるため、3元連立1次方程式を解くことで簡便的な極限解析を行うことができる。なお、安全率が1を下回った積分点については
3.3節で説明した荷重増分法における山田の方法あるいは
3.4節で説明した反復法により塑性計算を行う。破壊条件がモール・クーロンの場合、これら両者の関係は
図5.26に示すようになる。図のように、ここでの反復法では、せん断応力のみを解放力として扱っており、山田の方法と比較すると若干誤差が含まれるものと思われるが、すべり面における間隙水圧や引っ張りクラックなどを容易に取り込むことが可能である。
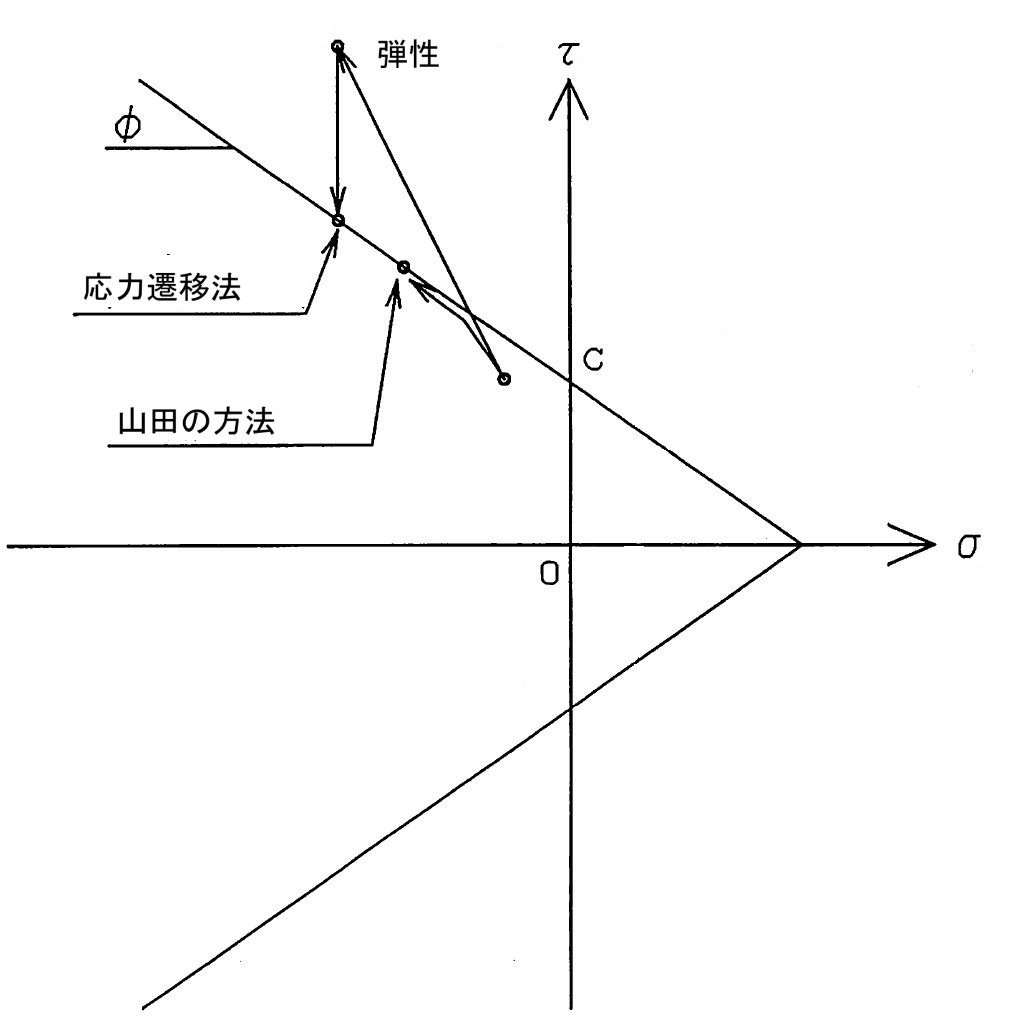
$\hspace{10em}$図5.26 応力経路の概念図
図5.27はモデル斜面において、弾性計算、山田の方法および反復法による計算を行い、各々の方法の最小安全率を与える位置と最小安全率の値を示したものである。なお、地盤は均ーで、材料定数は図中に示す通りである。また、本計算では間隙水圧を考慮していない。反復法と山田の方法による最小安全率を与える円弧中心位置は法先を原点として $(-0.5{\rm m}、12.0{\rm m})$ の位置にあり、最小安全率も $F_s = 1.45$ と全く同じである。一方、弾性計算の最小安全率の位置は図に示すよう、塑性計算の場合と異なり、また最小安全率についても約6%小さい値となっている。
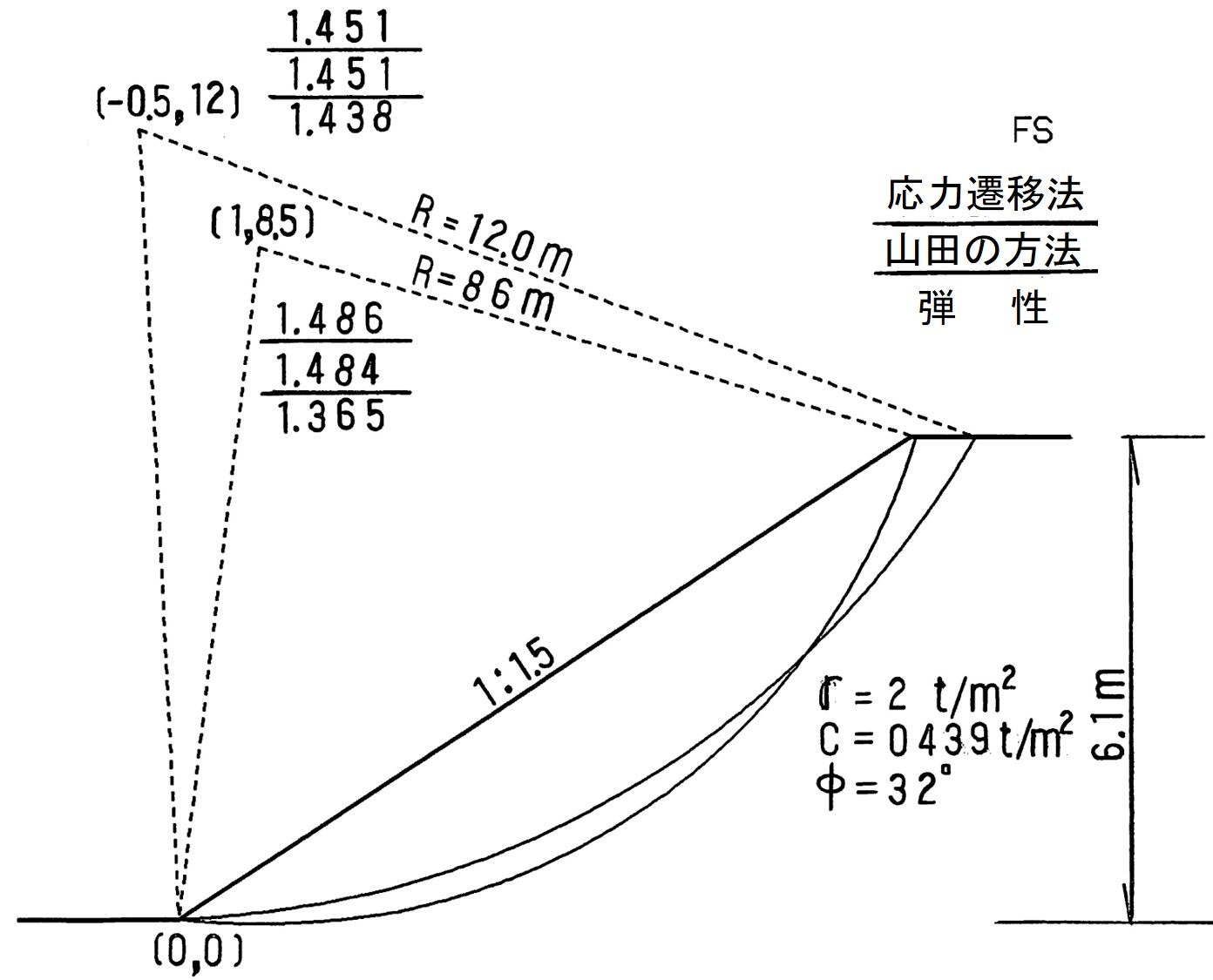
$\hspace{6em}$図5.27 最小安全率を与える円弧
図5.28に塑性計算で得られた最小安全率を与える円弧すべり線上の局所安全率の分布状況を示す。塑性計算では円弧すべり線の安全率は平均化されており、法先付近では $F_s=2.5$、法肩付近では塑性化しているため $F_s=1.O$ となっている。また、反復法と山田の方法では円弧上のすべり線に若干の差異か見られるが、安全率はほとんど同じ値となっている。
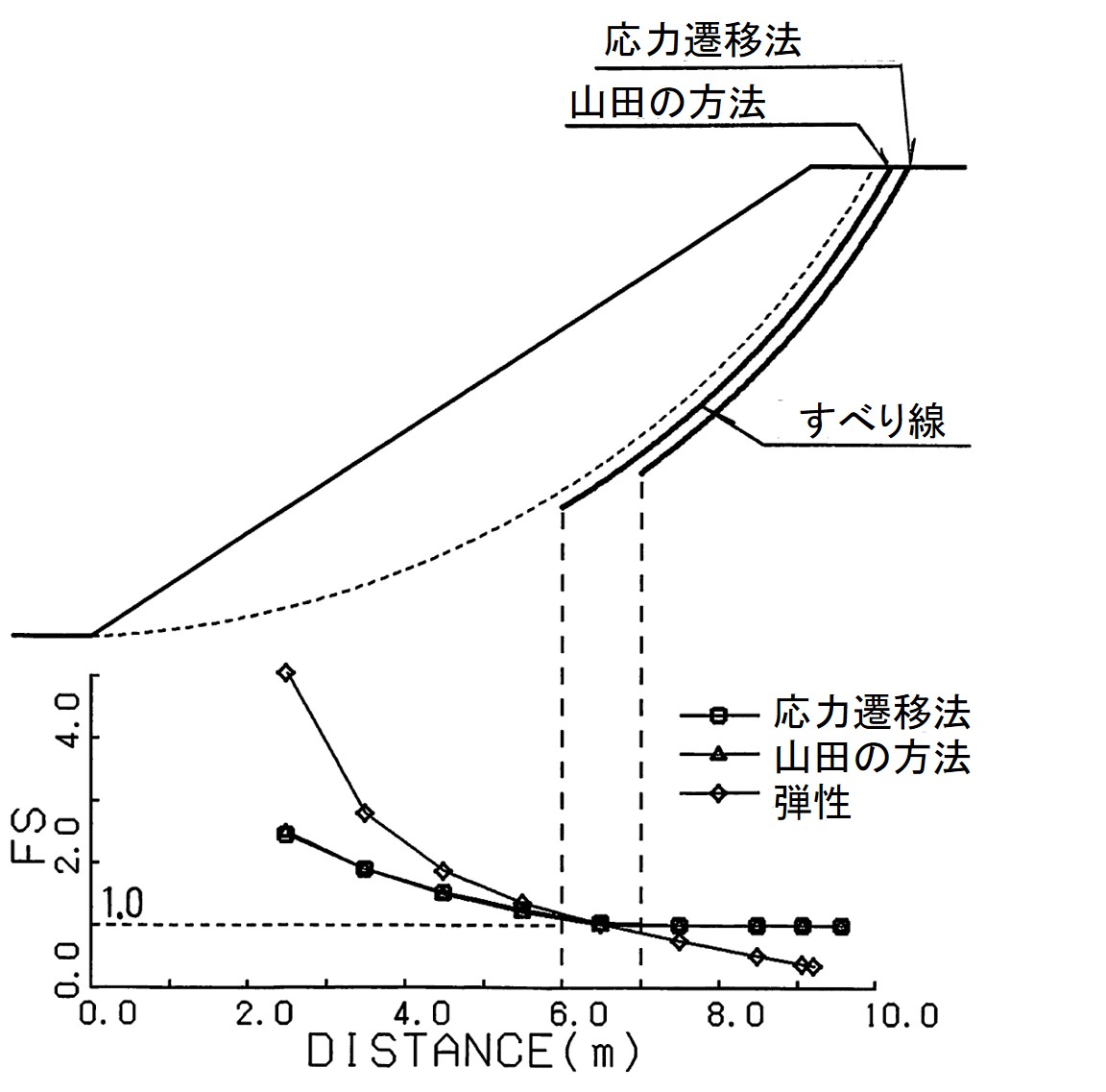
$\hspace{4em}$図5.28 局所安全率の分布状況
次に反復法による結果とFelleniuse法、Bishop法による結果を比較してみよう。
図5.29は各々の方法により最小安全率を与える位置を求め、比較した図である。Bisbhop法とRBSMを比較すると円弧の中心は川井モデルが $(1.3{\rm m}、83.O{\rm m})$、Bishop法が $(4.1{\rm m}、75.9{\rm m})$ と比較的近い位置にあり、安全率も川井モデルが $F_s=1.160$、Bishop法が $F_s=1.155$ と同様な値を示す。一方、簡便法 (Fe! leniuse法)による最小安全率を与える円弧中心位置は両者と大きく異なり、安全率の値も小さくなっている
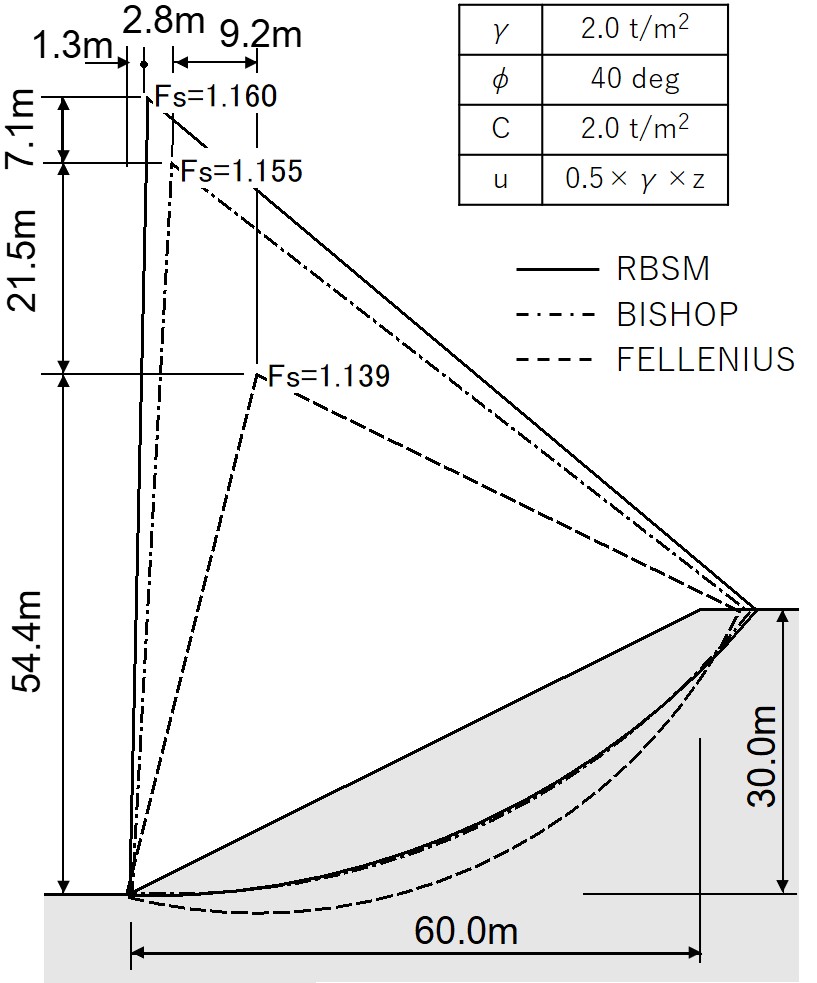
$\hspace{6em}$図5.29 従来法との比較
図5.30は各方法における安全率の位置的変化を調ぺたものである。横軸が円弧中心の $x$ 座標、縦軸は $y$ 座標である。この図より、川井モデルによる安全率はBishop法よりやや高めの値を示しているが、円弧の中心が法面に近づくにしたがって安全率が増化する傾向は同じであることが理解できる。簡便法は法面に近づくにしたがい、これらと逆に安全率が滅少する傾向にある。
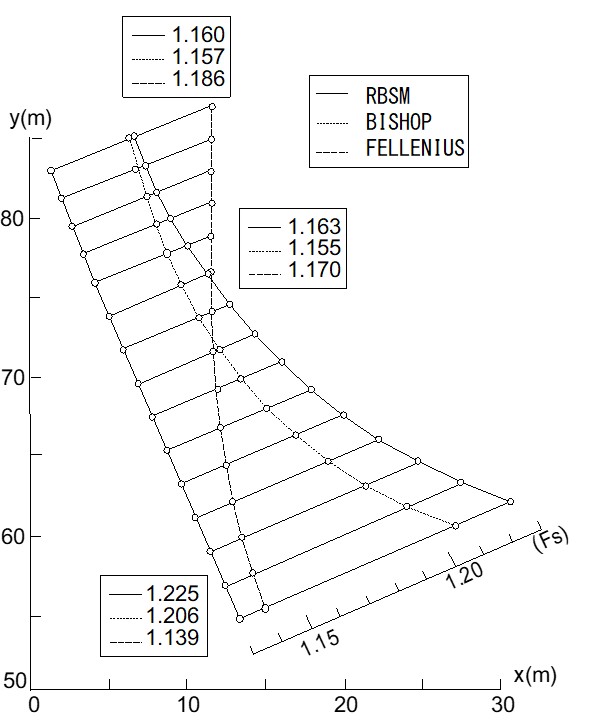
$\hspace{3em}$図5.30 安全率の位置的変化
以上の方法は円弧を1要素で考えているため、細片分割間に生ずる不静定カを扱うことができない。一般的には、法肩に引っ張り破壊が生ずることも多く、細片間に生ずる表面力を評価する必要がある。そこで、先の方法をさらに発展させ細片間の不静定力を評価できる方法について説明する。先の方法と同様、基本的な計算手順から説明しよう。
- ① 斜面の形状や地層線のデーターを与え、領域内を細片に分割し、これを基に円弧で囲まれた各々の細片における地盤の重童を計算する。この過程は先の方法と同じである。
- ② 図5.31(a)に示すよう、各細片を川井モデルにおける1つの要素と考え、●印間を積分区間、○印を積分点に設定する。この作業も先の方法と同様、プログラム内で行うことができ特別な入カデーターは必要としない。
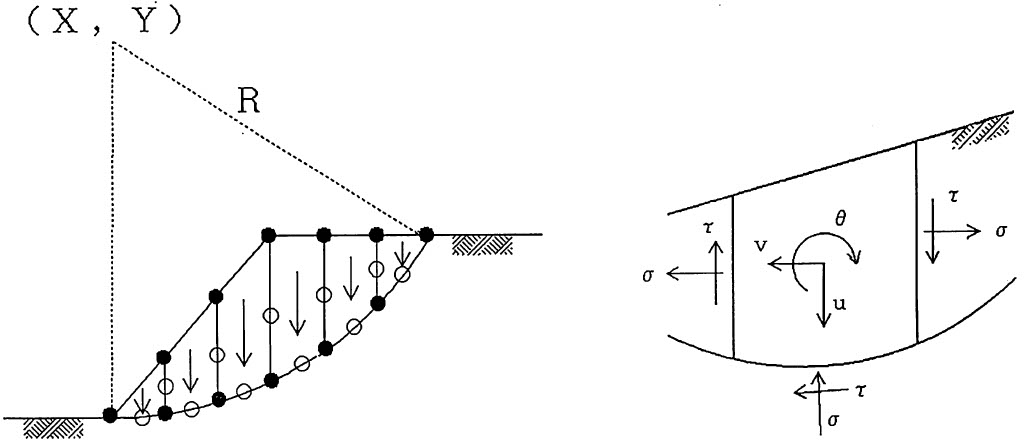
$\hspace{7em}$(a)
$\hspace{12em}$(b)
$\hspace{7em}$図5.31 細片分割と自由度設定位置
- ③ 図5.31(b)に示すよう、川井モデルの自由度設定位置を各細片の重心にとり、平行変位 $(u, v)$ と剛体回転角 $(\theta)$ の3自由度をそれぞれの細片に設ける。各細片毎に剛性行列を作成し、全体系に重ね合わせる。地盤の剛性の考え方は先の場合と同じである。
- ④ ①で求めた重量により各細片に対応する外力項を作成する。
- ⑤ 川井モデルによる離散化極限解析を行い、図5.31に示すよう、各積分点における単位面積当たりの表面力を計算する。
- ⑥ ⑤で得られた表面力から各積分点での安全率を計算し、斜面全体の安全率を先の場合と同様に求める。
このように各細片間に積分点を設けているため、この点の不静定力が自動的に求められる。なお、塑性計算については、先の場合と全く同じに考える。
図5.32には計算に用いた均一斜面と反復法、山田の方法による塑性解析ならびに弾性解析による細片間の不静定力を比較した図が示されている。弾性解析では水平方向の力 $E$ が法肩に近づくに従ってかなりの領域で引っ張り力が発生しているが、塑性解析を行いすべりを発生させると、応力再配分によりこの領域が極端に少なくなる。山田の方法では、まったくなくなっている。また鉛直方向の力Tに対しても、弾性解析では極端なせん断力の変化が認められるが、すべりの発生により変化の度合いが緩和されている。これは、他の簡便法による結果と類似した傾向である。
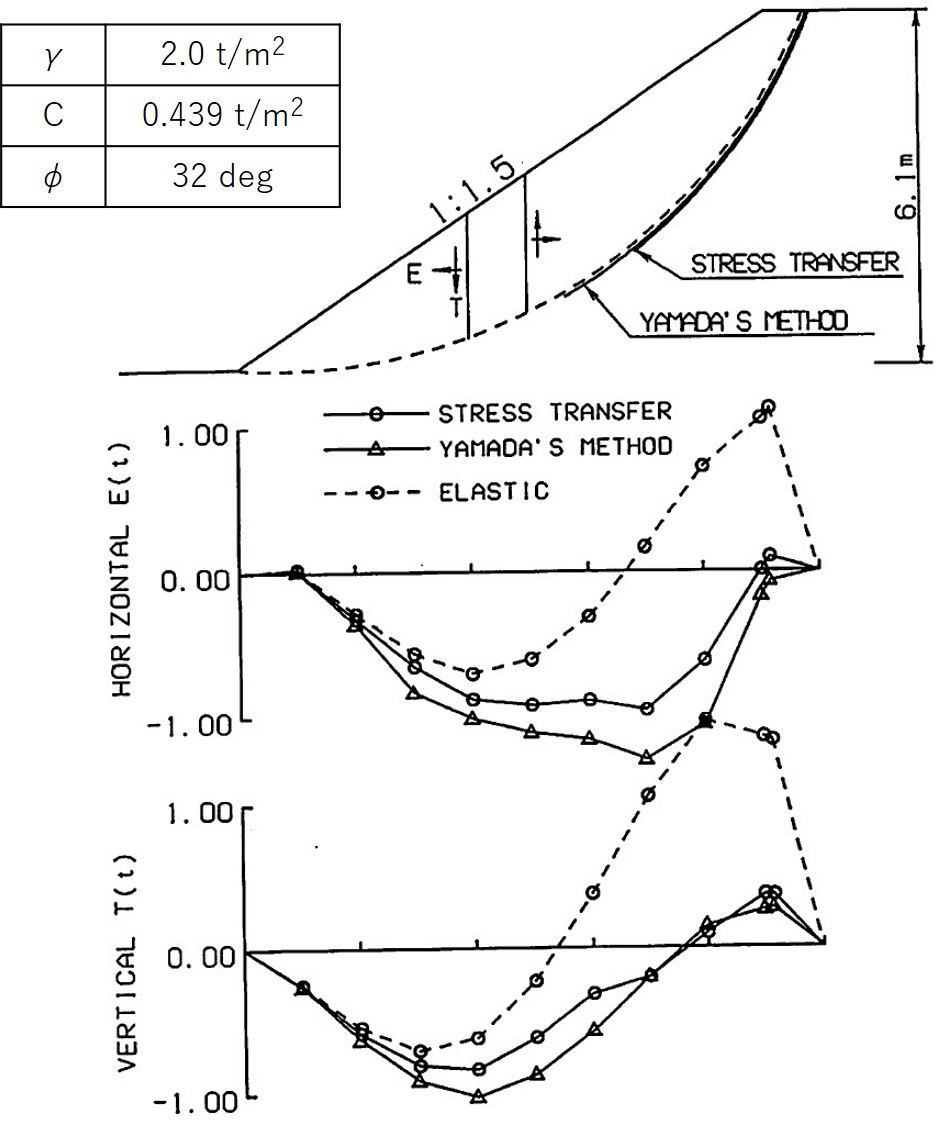
$\hspace{6em}$図5.32 不静定力の分布
図5.33は反復法において引っ張り破壊を考慮した場合の引っ張りクラック発生位置の妥当性を検討した結果が示されている。高さ $H$、傾斜角度が $30^{\circ}$ の斜面において、地盤の内部摩擦角が $20^{\circ}$ で非排水状態にある場合、限界破壊円の中心は法先を原点として $(0.2H、1.85H)$ にあり、限界引張亀裂の位置は法肩より $0.1H$ の位置にある。図は、H=lOmとした場合の結果であり、引張破壊の位置は法肩より $0.68{\rm m}(0.07H)$ の位置にあり、引張破壊を起こした1箇所の底部よりすべり線が発生している。
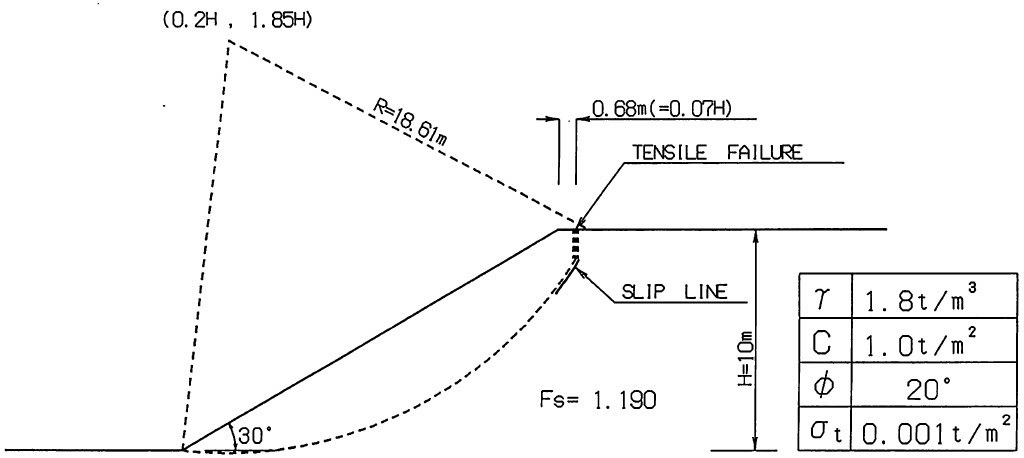
$\hspace{8em}$図5.33 引っ張り破壊の発生位置
表5.2は各解析法による安全率をまとめたものである。ただし、簡便法の安全率は望月らが行った値である。川井モデルによる安全率と他の方法による安全率の関係は、先の1要素タイプの場合と同様な傾向を示している。
表5.2 各解析法における安全率
| 解 析 法 |
安 全 率 |
| FELLENIUS法 |
1.43 |
| BISHOP法 |
1.54 |
| JANBU法 |
1.63 |
| 弾性解析 |
1.408 |
| 弾塑性解析(山田の方法) |
1.456 |
| 弾塑性解析(反復法) |
1.451 |
| 弾塑性解析(反復法:引張破壊考慮) |
1.453 |
このように、従来の分割法におけるデーターを共有し、特別なデーターを入力せずに安定解析が行えるため、試行計算には便利に利用できる。また、複雑な要素分割を必要としないため、簡便的な3次元斜面安定解析も容易に行うことができる。
































