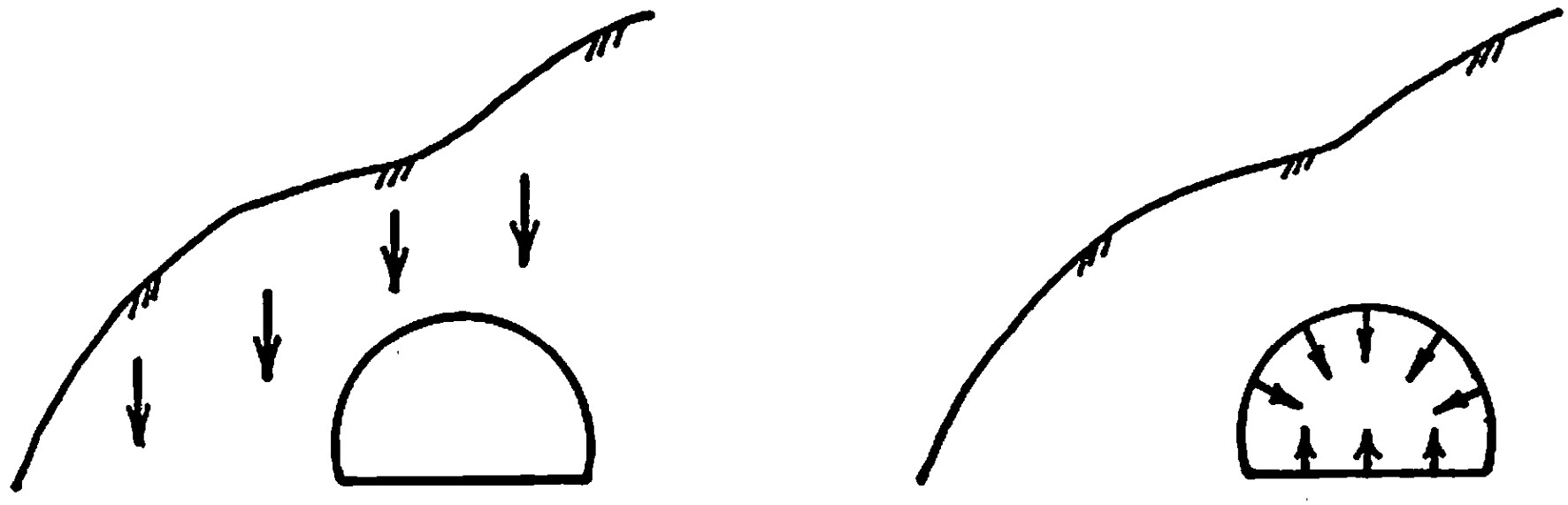擁壁や矢板、トンネルなどを設計する際、最も重要な外力として土圧をあげることができる。土圧は地盤工学における重要課題の1つとして古くから研究されてきた。しかし、土圧の性質は地山の構成状態やその材料学的な性質に支配されるばかりでなく、地下水の変動や地中構造物の剛性によって大きく異なるため、信頼性の高い土圧計算法を確率するのは極めて難しい。現在、設計で用いられている土圧は塑性状態の力の釣合から得られたものが中心となっている。
構造物を設計する場合、簡便的に土圧を外力として取り扱い、構造物のみに着目し解析することがよく行われている。しかし、近年では有限要素法のような数値解析法の発達とともに構造物と地盤を連成させ、同時に解析することが行われるようになってきた。この場合、問題となるのが地盤と構造物が接触する面の取り扱いや構造物そのもののモデル化である。
有限要素法では構造物と地盤の接触面にジョイント要素などの特別な要素を取り込み、解析が行われている。一方、川井モデルでは、もともと要素境界辺上に設けたばねを用いてエネルギーを評価しているため、このばねに接触特性を与えれば、2重節点とするような特別の要素を持ち込まなくてもよい。このような接触面を含む連成問題の非線形解析法としては
3.5節において説明した引張破壊を考慮したアルゴリズムが利用できる。
一方、2次元問題における地中構造物のモデル化の方法として平面要素を用いる方法と梁要素を用いる方法の2通りがある。以下にそれらのモデル化の方法について説明しよう。
(1)平面要素によるモデル化
例えば、擁壁やトンネルの覆工、大口径の杭などでは、解析領域の大きさにも依存するが、一般的に無視できない程度の厚さがあることも多い。このような場合には平面要素を用いて要素分割に取り込み解析する必要がある。
図6.1はトンネル覆工の要素分割例で、覆工を三角形要素により分割している。構造物の変形をある程度評価するためには、この例のように三角形要素などを用いて分割するのがよい。これは、川井モデルの場合、要素自身は剛体であると仮定しているため、四角形要素などを用いて少ない要素により構造物を表現すると剛体挙動が卓越し、詳細な変形が求められないからである。
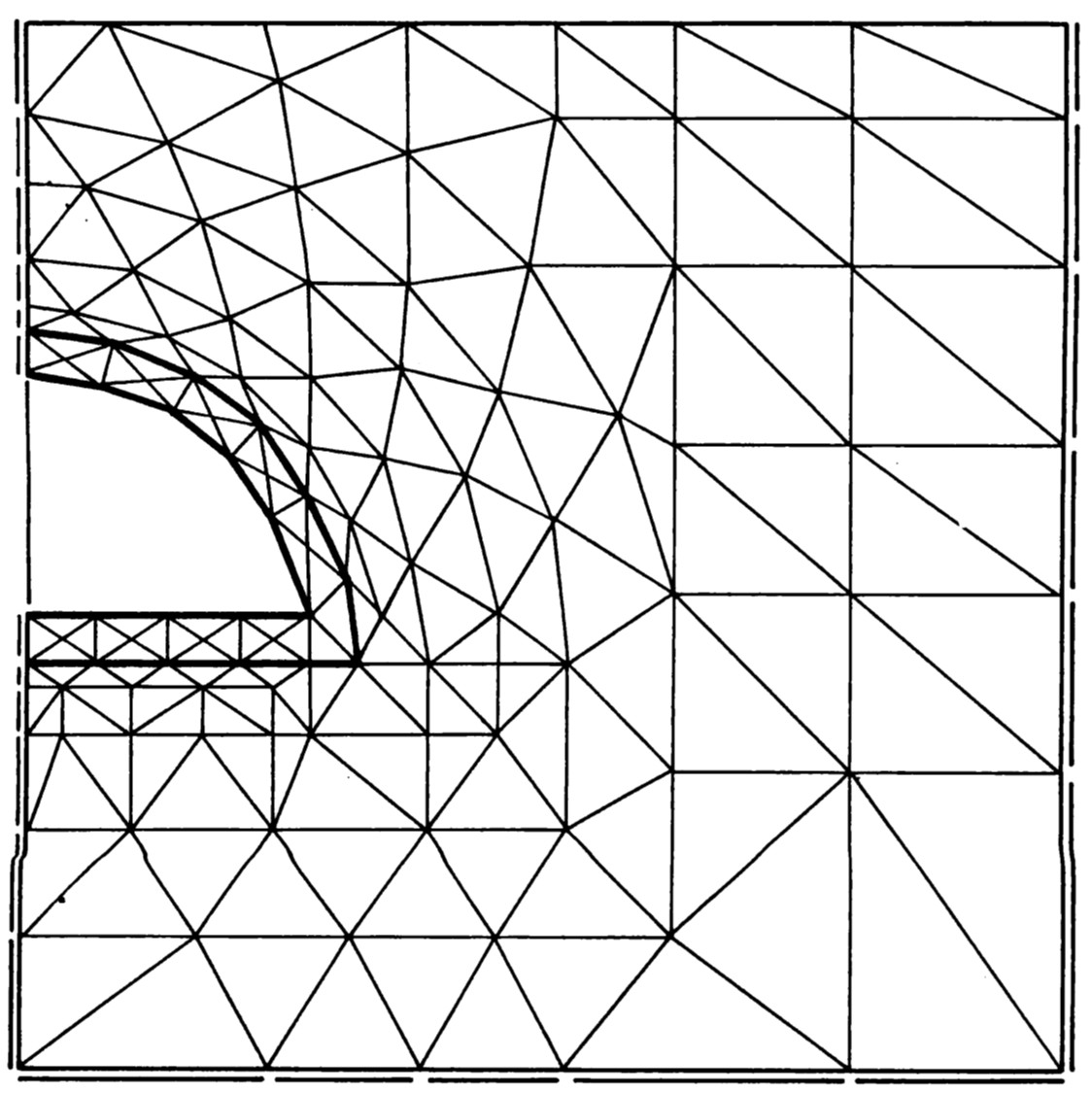
$\hspace{0em}$図6.1 平面要素を用いたトンネル覆工の要素分割
一方、斜面内にある擁壁のように、厚さはあるものの、構造としての変形ではなく、剛体としての挙動を掴みたい場合などでは、
図6.2(a)のように構造物を1つないしは数個の要素により表現することも可能である。しかし、擁壁のたて壁に生ずる曲げモーメントを知りたいなど、それほど構造物の変形量については問題としないが、内部の断面力を知りたいという場合には
図6.2(b)に示すよう四角形要素を用いた粗い要素分割を利用するとよい。

$\hspace{4em}$(a) 一要素
$\hspace{5em}$(b) 粗い要素
$\hspace{5em}$図6.2 構造物の粗い要素分割
川井モデルの平面要素は要素形状に関係なく、要素重心に $(u, v, \theta)$ の3つの自由度を持ち、各要素境界辺上に
図6.3左に示すよう、垂直、せん断に抵抗するばねが設定されている。これを要素境界辺に沿って積分すると
図6.3右のように垂直、せん断、回転に抵抗する3つのばねにより表現することができる。
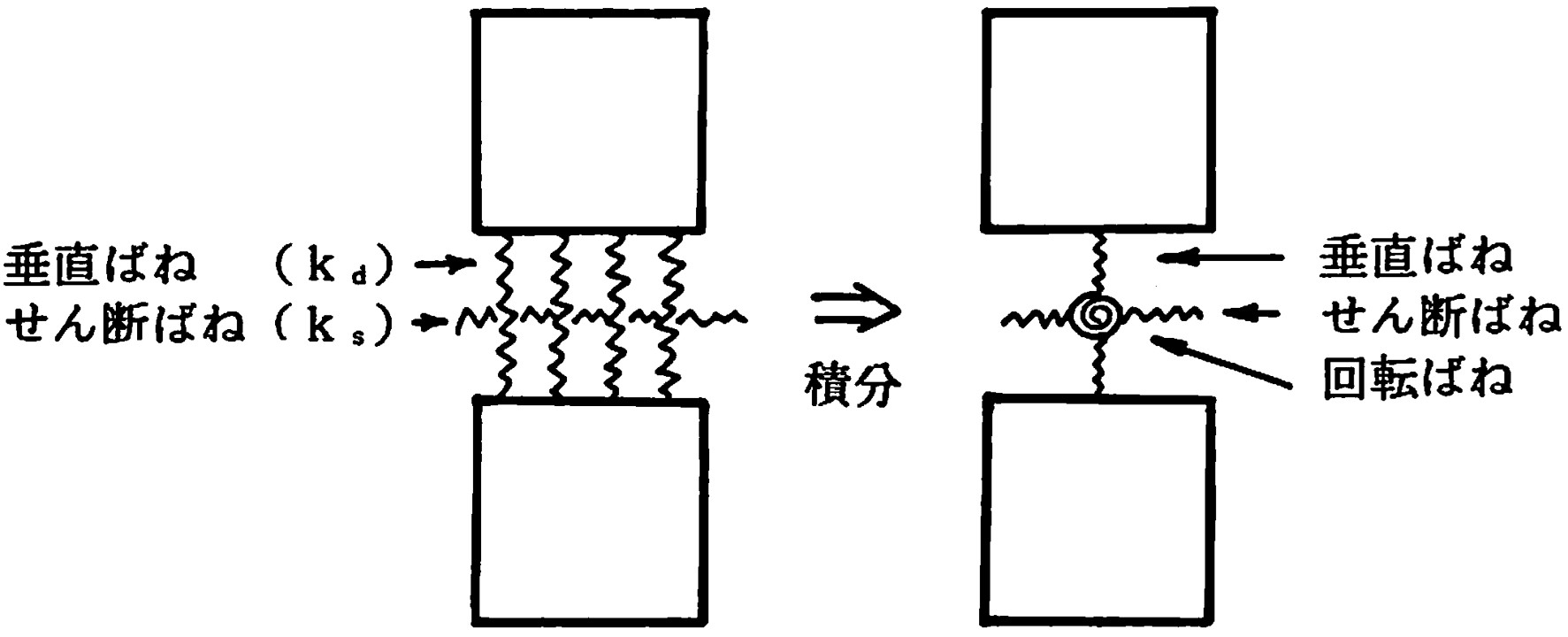
$\hspace{5em}$図6.3 ブロック境界面のばね
このばねと2要素間の相対変位ならびに相対回転角を用いれば、容易に2つのブロック間に発生する軸力、せん断力、曲げモーメントを求めることができる。
\[{\rm (6.1)}
\left.
\begin{array}{rcl}
N & = & \displaystyle \int_{ - \frac{L}{2} }^{ \frac{L}{2} }
( k_{n} \cdot \delta \overline{v} ) ds
= k_{n} \cdot \delta \overline{v} \cdot L \\[0.5em]
S & = & \displaystyle \int_{ - \frac{L}{2} }^{ \frac{L}{2} }
( k_{s} \cdot \delta \overline{u} ) ds
= k_{s} \cdot \delta \overline{u} \cdot L \nonumber \\[0.5em]
M & = & \displaystyle \int_{ - \frac{L}{2} }^{ \frac{L}{2} }
( k_{n} \cdot S \cdot \delta \overline{ \theta } ) Sds
= \frac{k_{n}L^{2}}{12} \cdot \delta \overline{ \theta } \cdot L \nonumber
\end{array}
\right\}
\]
\[\hspace{6em}
k_{n} = \frac{(1-\nu)E}{(1+\nu)(1-2\nu)h} \;, \;\;\;
k_{s} = \frac{E}{(1+\nu)h}
\]
ここで、$L$ は要素境界辺の長さを、$h=h_1+h_2$ は、それぞれの要素重心から要素境界辺に下した垂線の高さ,また,$\delta$ は相対的な変形を意味する。
この考え方は
図6.1に示したような三角形要素の場合にも適用できるが、局所座標系の相対変位を利用しているため、得られた断面力がどのような角度の切断面に対するものかに注意を払わなければならない。
(2)梁要素によるモデル化
矢板やトンネル支保工、ロックボルト、アンカーあるいは口径の小さい杭などは梁要素によりモデル化することがよく行われている。
川井モデルの場合、骨組要素から3次元要素までどの要素を組み合わせても自由度の変換を行わずに取り扱うことが可能である。簡単のため、2次元状態について説明しよう。
図6.4は川井モデルの平面要素と梁要素を示したものである。図のように川井モデルの2次元要素は平面要素、梁要素に関係なく、平行変位 $(u,v)$ と剛体回転角 $(\theta)$ の3つの自由度を重心に設定しており、隣接する2要素間に設けたばねによりエネルギーを評価する。すなわち、平面要素と梁要素の間に自由度の変換はまったくなく、要素間のばねの定義が異なるだけである。
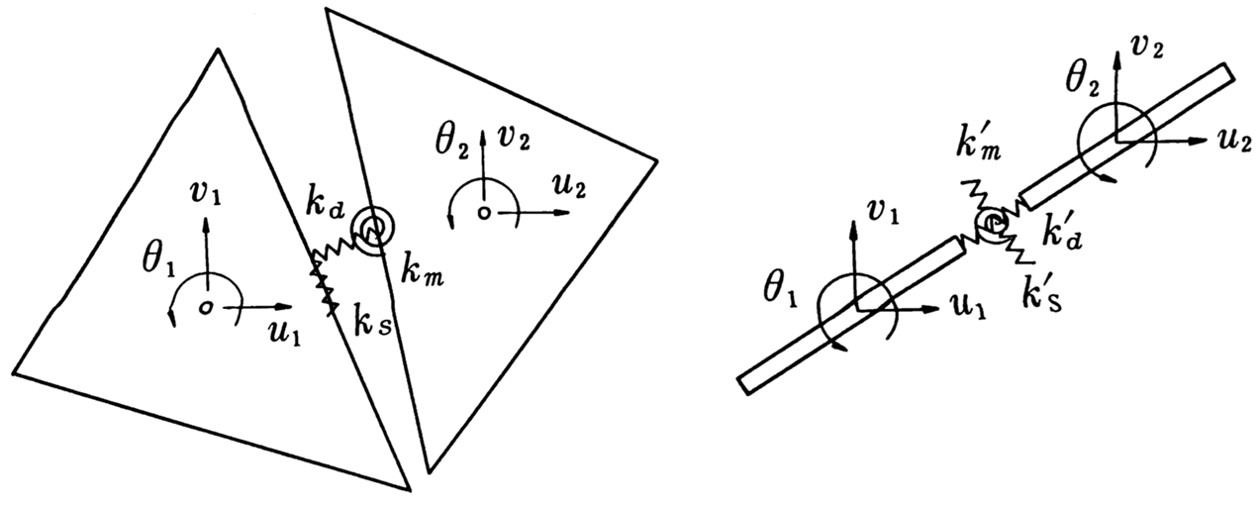
$\hspace{8em}$(a) 平面要素
$\hspace{10em}$(b) 梁要素
$\hspace{7em}$図6.4 川井モデルの2次元要素
したがって、種類の異なった2つの要素を組み合わせて解析する場合には
図6.5に示すよう、要素間のばね定数についてのみ配慮すればよい。図では、ダッシュの付いたばね $(k')$を梁要素のばね定数とし、ダッシュのないばねを平面要素のばね定数としている。図のように平面要素と平面要素、あるいは平面要素と梁要素の間のばねを平面要素のばね定数に、また、梁要素と梁要素の間のばねを梁要素のばね定数に設定すれば容易に梁要素と平面要素を組み合わせて解析することが可能である。
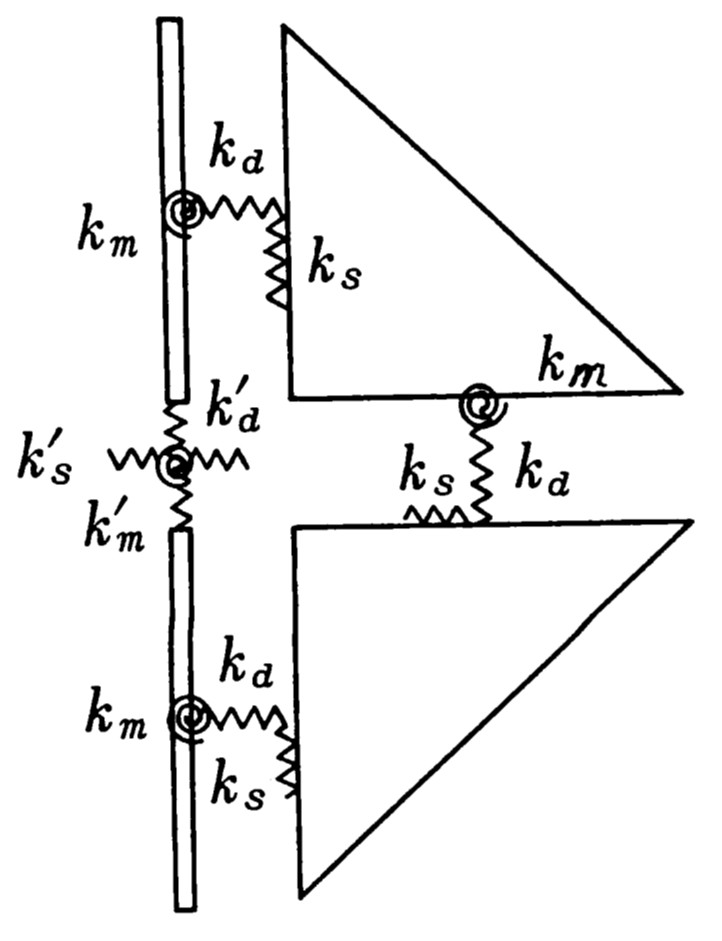
$\hspace{1em}$図6.5 平面要素と梁要素のばね
さて、同じ梁要素を用いてモデル化を行う場合においても、対象とする構造物によって要素間に設定するばねの発生方法が異なる。
図6.6は代表的なばね発生方法を示した図である。
図(a)は矢板や支保工、覆工などのように、構造物によって地盤が分断されているような状態を想定しており、この場合、平面要素と梁要素の間のばねは図のように(平面-梁-平面)間に設けられる。したがって、平面要素どうしはばねで結合されていないことになる。
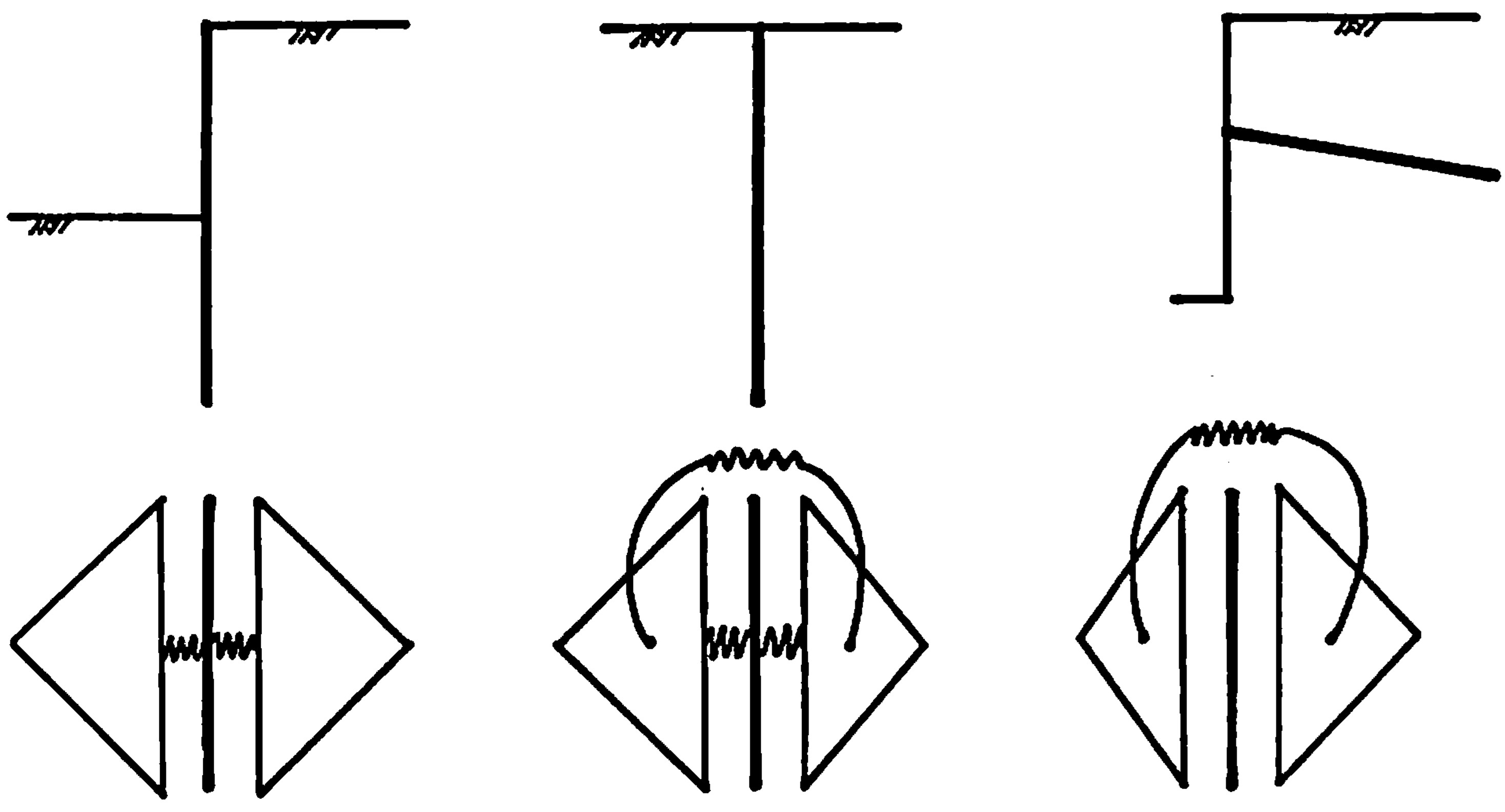
$\hspace{3em}$(a) 矢板
$\hspace{4em}$(b) 杭
$\hspace{4em}$(c) アンカー
$\hspace{3em}$図6.6 構造物の相違によるばねの発生方法
一方、杭やロックボルトのように奥行き方向の地盤に対して、一部に梁要素がある場合には
図(a)の状態に加え、平面要素と平面要素を結合するばねを発生させる必要がある。この関係を示した図が
図(b)である。この場合、地盤と構造物がばねにより接合されているため、接触問題としての取り扱いが可能であるが、逆に、アンカーなどのように接触効果が期待できない場合には
図(c)のように梁要素と平面要素間のばねを設定しなければよい。このように考えれば、梁要素と平面要素の節点が同一節点とならないよう要素分割を行う従来の方法に比べ簡単に要素分割が行えるようになる。
以上モデル化に関する注意事項について説明したが、次節以降に具体的な解析例を用い離散化極限解析に関する注意点を述べる。
一般に擁壁の安定性を確保するため、擁壁の転倒、すべり、基礎の支持力と沈下の3つの安定性について検討する。これらの安定計算は擁壁自身の局所的なものによるところが強いが、擁壁を含む斜面全体としての安定性が問題となる場合も度々生ずる。
実設計で多用されている簡易法的取り扱いでは各種の安全性を個々に検討しているが、複雑な地盤では、それぞれの要因が影響しあい複雑な挙動を示すこともまれではない。特に擁壁に作用する土圧分布は地盤の破壊形態と密接な関係があるものと思われる。本節ではこのような問題に川井モデルによる離散化極限解析を適用した例について説明する。
擁壁をモデル化する場合、前節において説明したように、平面要素がよく利用されている。ここでは、この擁壁を比較的粗い要素に分割した場合の例を示めす。
図6.7は解析に用いたモデルが示されている。境界条件は図に示すよう、周辺スライドとした。材料定数は図中に示す通りで、擁壁自身の破壊は無視している。また、擁壁と地盤の接触面における摩擦係数は地盤と同じ内部摩擦角 $\phi = 30^{\circ}$ より求めるものとしている。
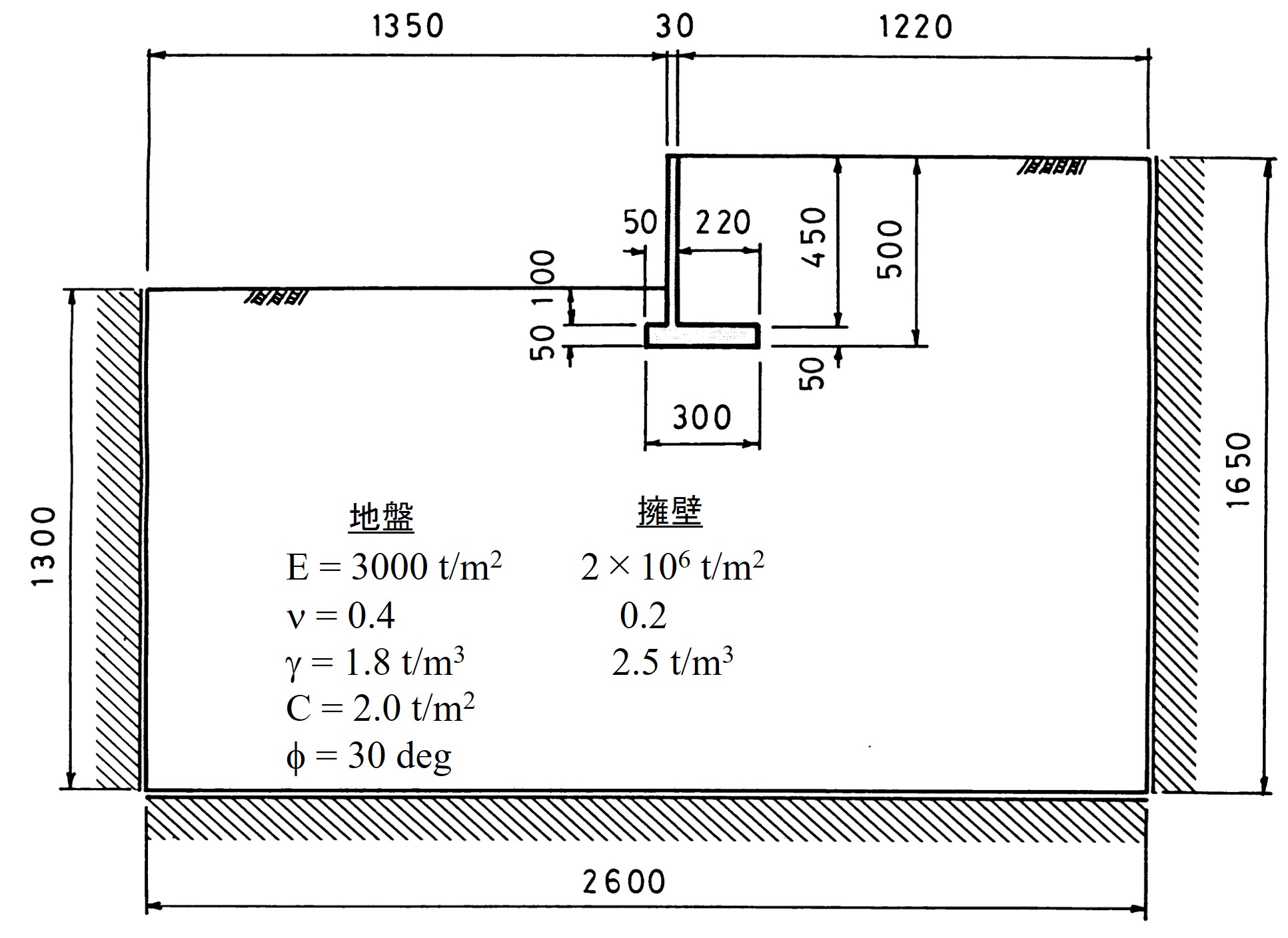
$\hspace{4em}$図6.7 擁壁の安定解析のためのモデル
図6.8に要素分割図を示す。前節の
図6.1(b)に示したように、擁壁については後で曲げモーメントを計算しやすくするため、四角形ブロックにより分割している。
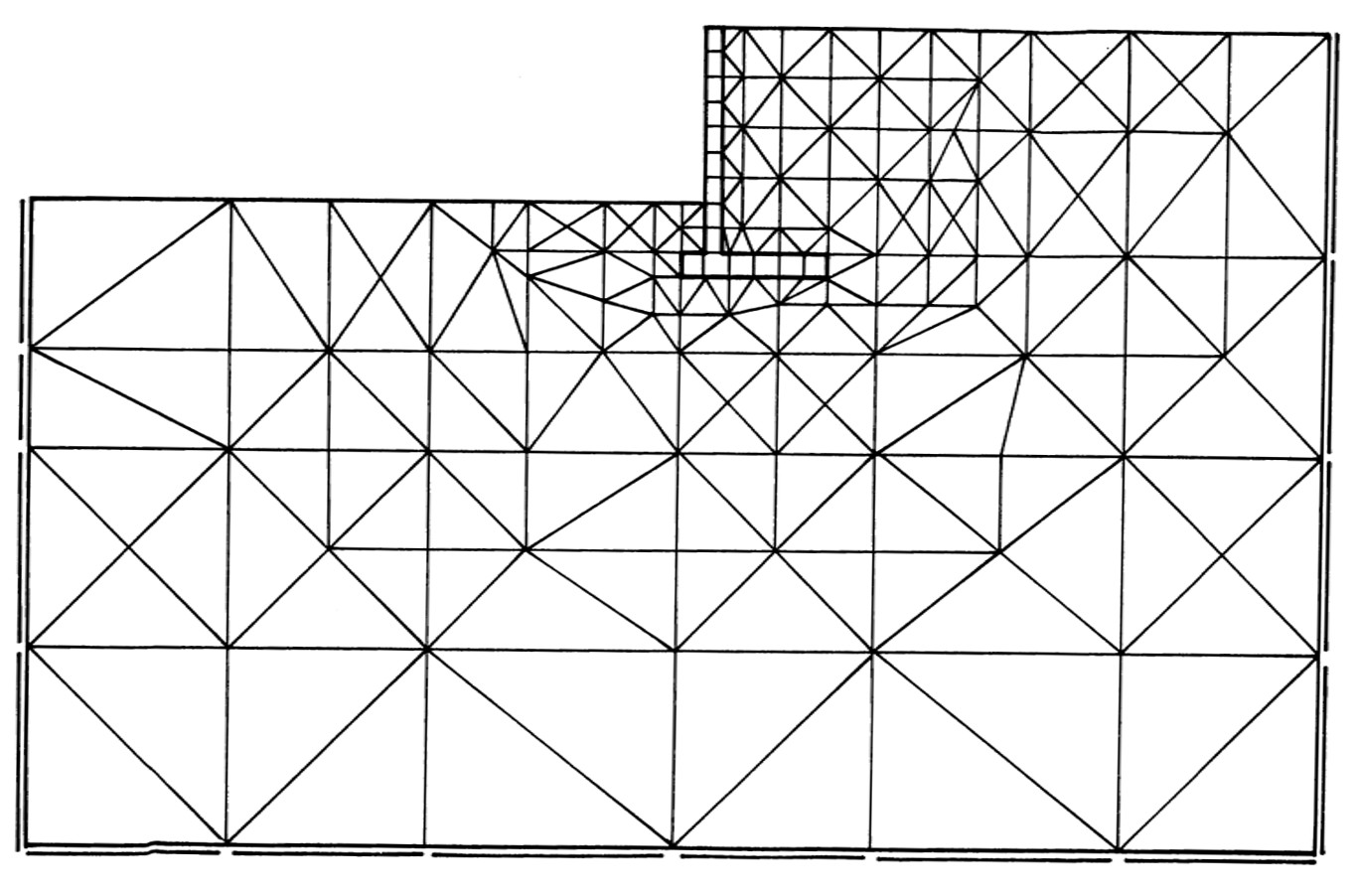
$\hspace{4em}$図6.8 擁壁を含む斜面の要素分割
図6.9は離散化極限解析によるすべり線が示されている。擁壁のつま先部分にすべり線が多く見られるが、擁壁背面にも多く発生し、一部は右の境界に達している。この例の場合、解析領域が若干小さすぎる傾向にある。全体的に眺めると、擁壁に近い地盤の浅い部分で円弧すべりによる破壊が進行する傾向がうかがえる。
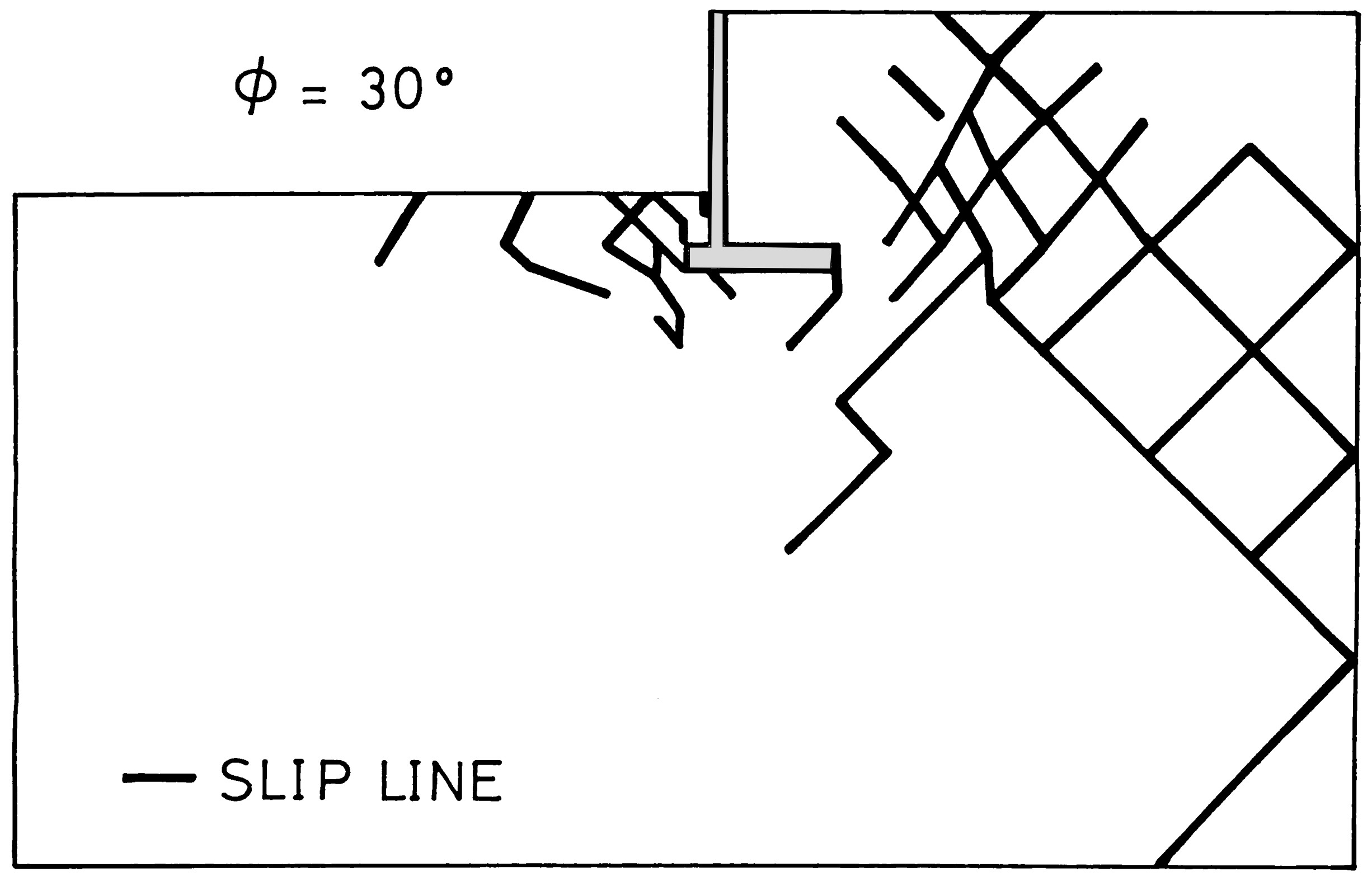
$\hspace{5em}$図6.9 すべり線発生状況
図6.10はこのときの変位モード、曲げモーメントならびに擁壁底部の地盤反力を示した図である。変位モードに関しても、すべり線から推定された地盤の浅い部分におけるせん断破壊の傾向が現れている。
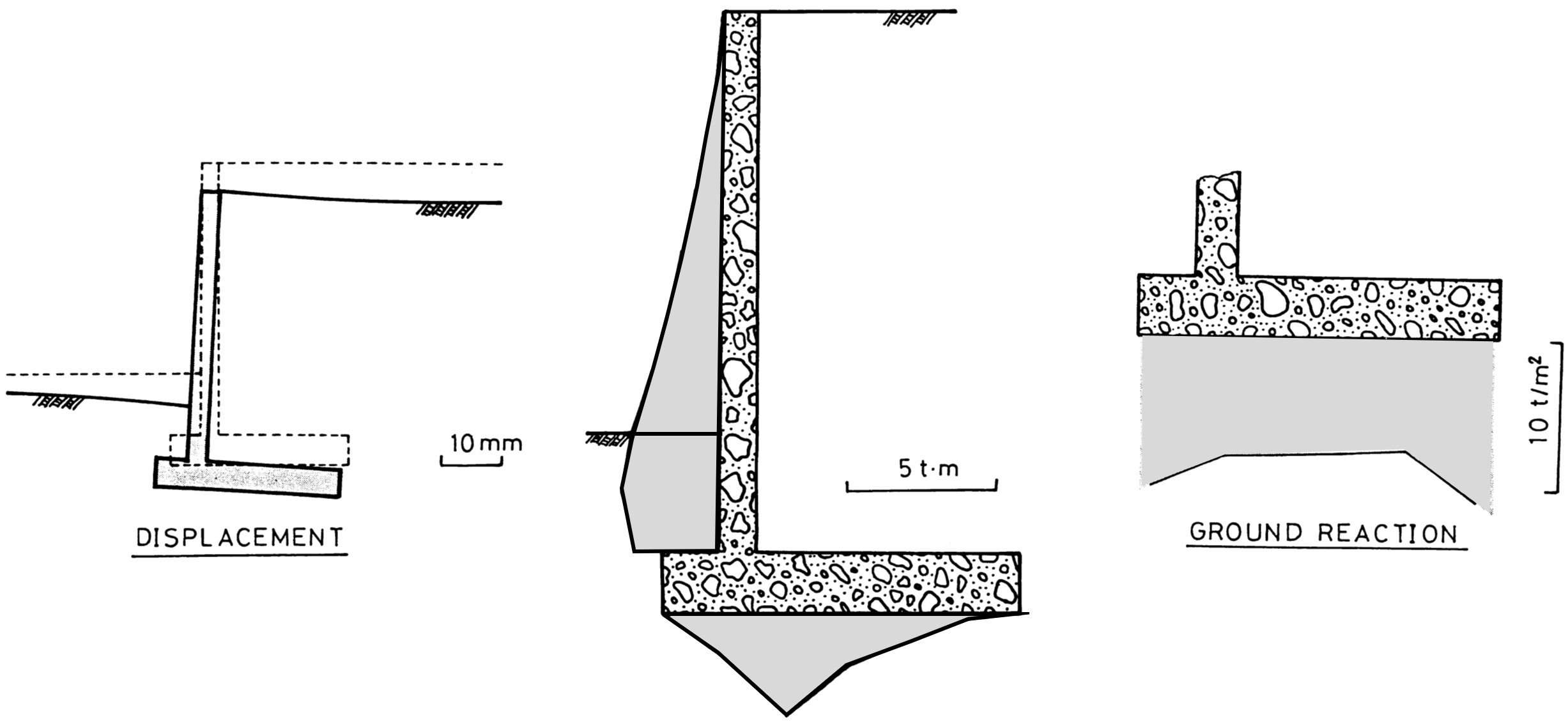
$\hspace{5em}$図6.10 擁壁の断面力と地盤の変形・反力
通常、たて壁の設計では、たて壁と底版との接合部を固定端とする片持ち梁とし、土圧の水平分力や水圧などによる分布荷重を作用させて計算する。この場合、曲げモーメントの最大値は接合部において生ずるが、本解析における曲げモーメント図を眺めると若干、接合部より上側で曲げモーメントの最大値が生じている。これは、1つにはつま先部分の上にある土砂の受働土圧に関係があるものと思われる。現在の設計は、そういった意味で安全側の設計方法となっているといえよう。
以上の例はモデル化された非常に簡単な例であるが、擁壁を含む斜面の安定解析と供に、擁壁自身の大まかな断面力が要素重心の剛体変位を利用することで可能となることが理解できたと思う。
開削工法により掘削を行うと、安定していた地盤が掘削による解放力によって破壊し、地盤構造物は不安定となる。したがって、掘削した空間を一時的に保持するための仮設構造物が必要となる。この仮設構造物は工事中の一時的なものであるが、港湾構造物などのように半永久的に利用されるものもある。
このような壁体には矢板や杭などが多く利用されるが、解析領域の広さから考えると極めて板厚が薄く、また、材料の性質も著しくことなるため、取り扱いが面倒になる。
この種の問題に対して、従来の簡便法では土圧分布を仮定し壁体のみの骨組構造解析を行ったり、また、地盤のみの安定解析を行うといった連成を考慮しない解析法が主流であった。しかし、地盤の地質構造が複雑で、特に重要な構造物や特殊な条件下における構造物ではさらに慎重な検討が必要であり、近年、連成問題としての解析が行われるようになってきた。
一般に、仮設構造物などをモデル化する場合、
6.1節で説明した梁要素を平面要素に組み合わせて利用する方法が用いられている。ここでは、2つの例を用いて、このことを説明する。解析にあたり初期地圧の設定が問題となるが、ここでは、簡単に
図6.11に示すような静止土圧係数により計算し、各要素境界辺に沿った局所座標系に変換した後、ばねに初期応力として与えた。
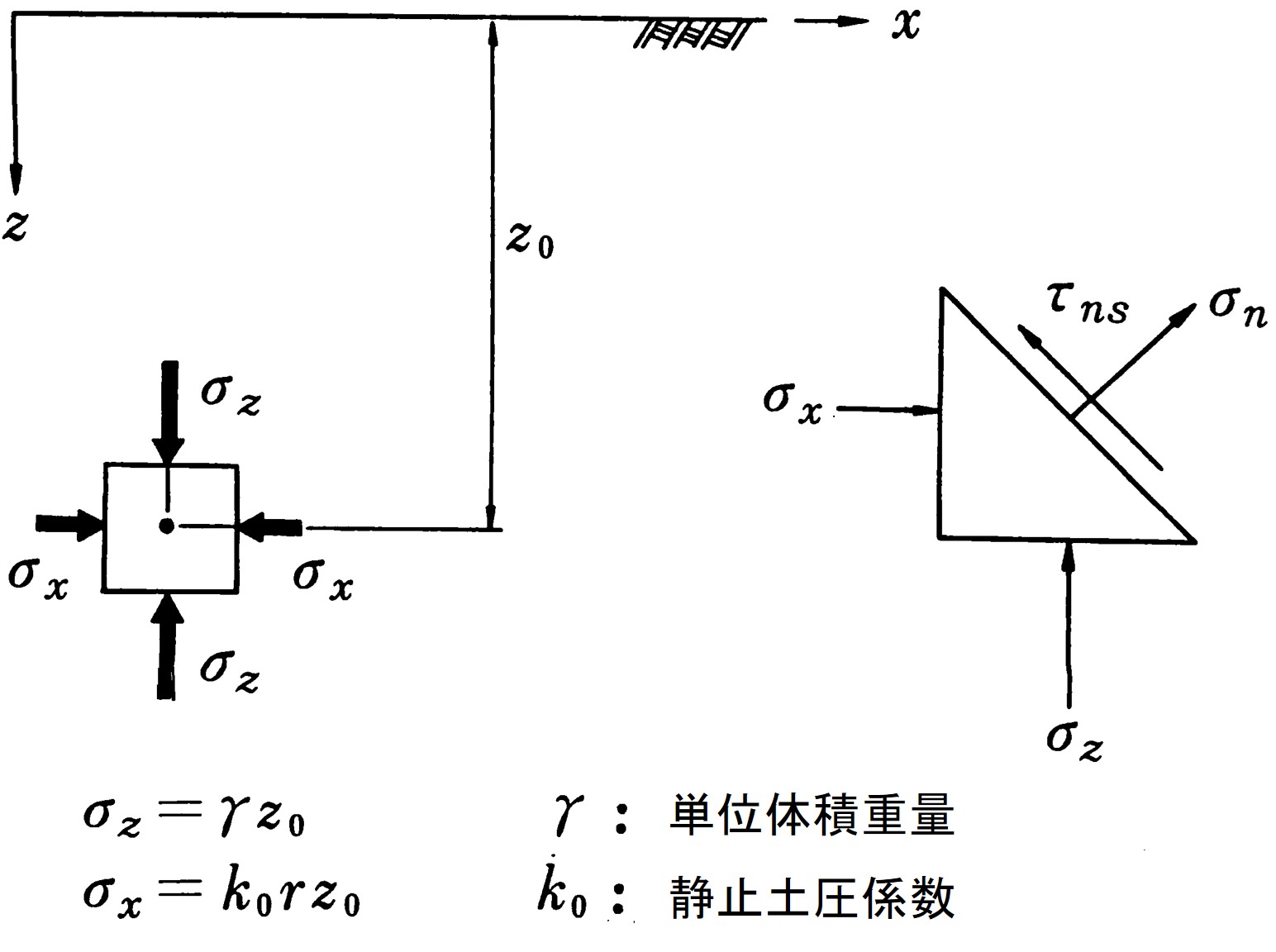
$\hspace{6em}$図6.11 初期地圧の仮定
一方、計算は掘削に伴い解放される力を外力として進める。この場合、掘削相当外力を求めなければならない。
2.4節において解放力の計算方法を示したが、掘削相当外力の計算もばねが所持していた表面力を解放するという意味で引っ張り破壊の場合と同じであり、
式(2.3)、式(2.5)を用いて計算することができる。
(1)自立式矢板の解析
初めに、簡単な例として自立式矢板の解析を示す。解析に用いたモデルが
図6.12に示されている。この例では、地盤の破壊条件としてモール・クーロンの条件を用い、矢板については弾性と仮定し、破壊しないものとした。解析に用いた材料定数は図に示す通りである。ただし、()で示された値は地盤と矢板の接触面上の値であることを表している。境界条件は周辺スライドとし、図中〇印で囲まれた番号の順に掘削し、その解放力を外力として計算を進める。
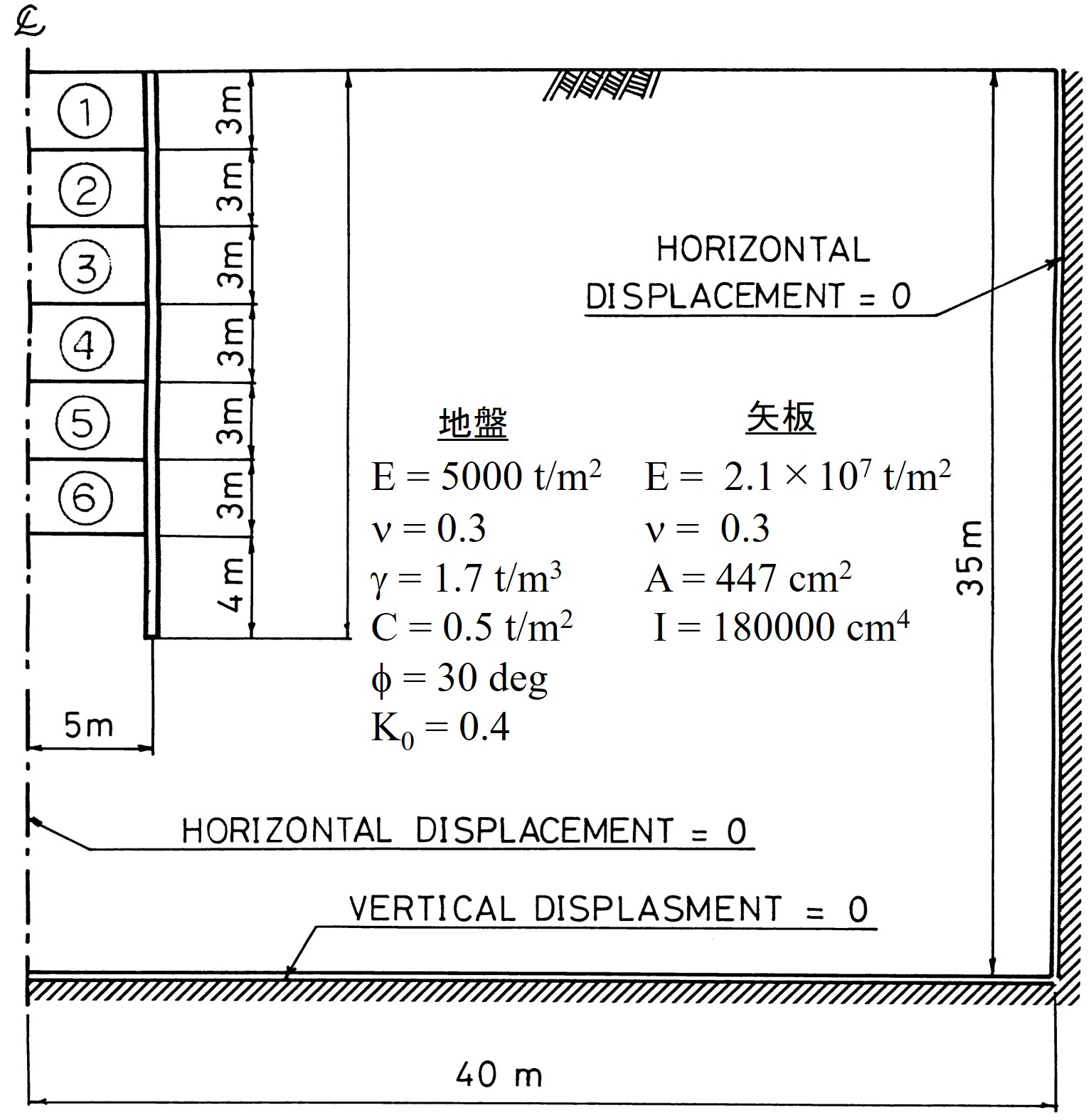
$\hspace{4em}$図6.12 自立式矢板の解析モデル
計算に用いた要素分割図が
図6.13に示されている。図中、矢板部分が四角形要素のように見えるが、これはこの部分に梁要素があるということを強調するために描いたもので、実際の要素分割では厚さはない。この要素分割で要素数311、総自由度933である。
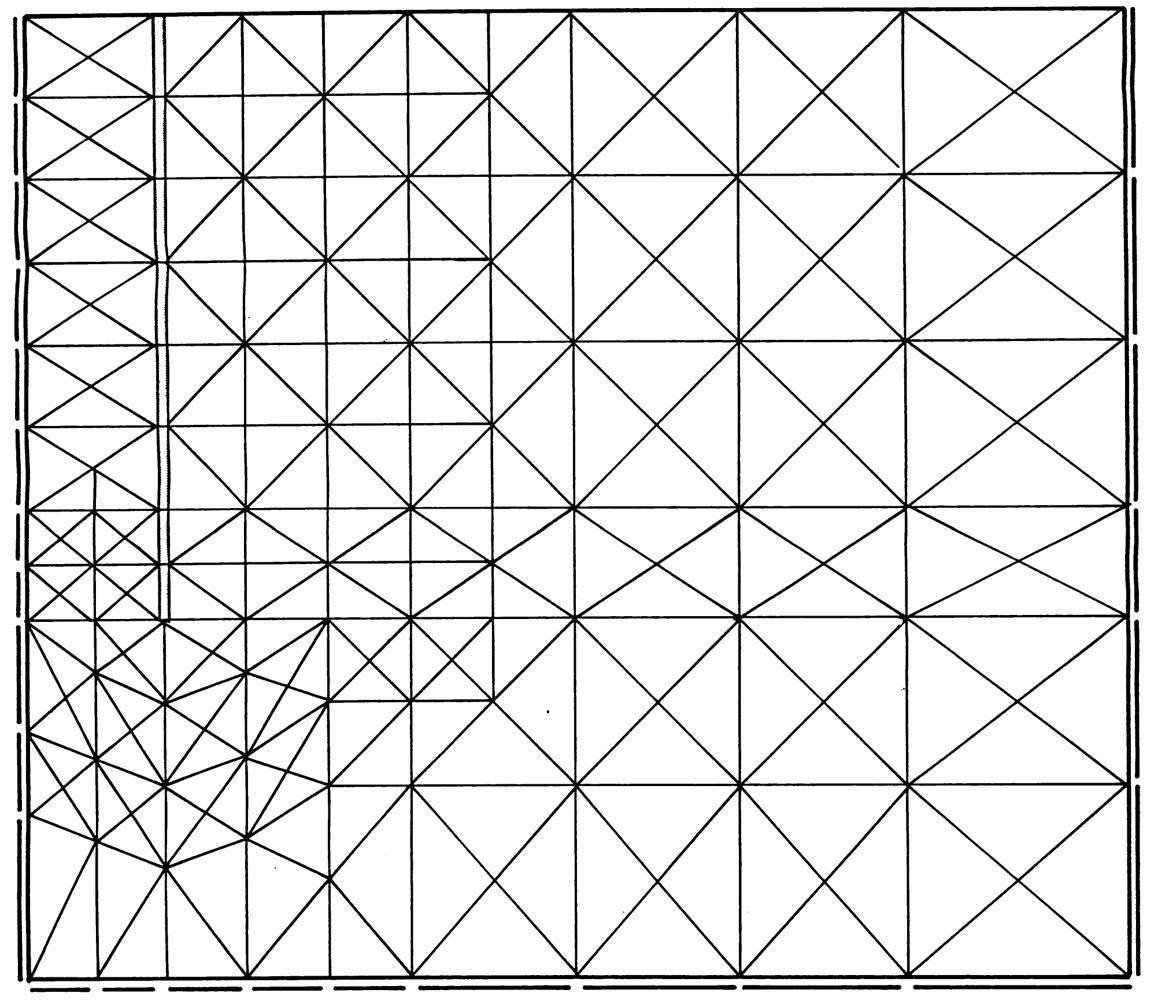
$\hspace{6em}$図6.13 自立式矢板の要素分割
図6.14は離散化極限解析によるすべり線パターンを各掘削ステージ毎に描いた図である。掘削が浅い段階では矢板と地盤の接触面近傍がすべる傾向が見られるが、掘削が進につれ矢板のたわみが大きくなり、矢板背面の地盤がRankinの仮定と同様なすべり線によりすべり出す。また、掘削底面の破壊も掘削の進行と供に著しい破壊を示し、矢板の自立を阻害する傾向が現れる。
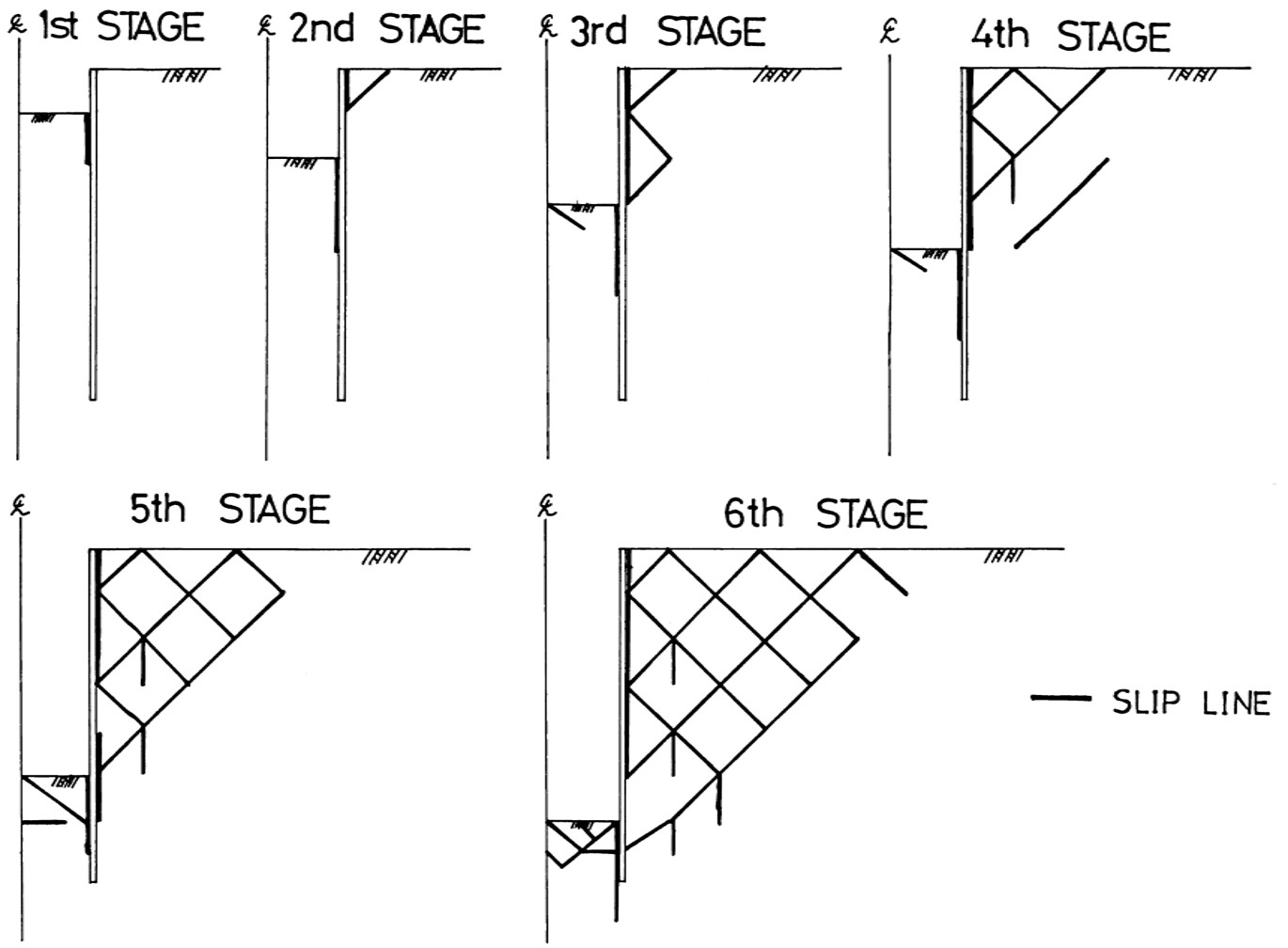
$\hspace{4em}$図6.14 自立式矢板のすべり線
図6.15はこのときの変位モードを示した図である。ただし、掘削ステージ毎に矢板のたわみ量に関するスケールが異なっているので注意してほしい。掘削当初は、矢板頭部がたわむ傾向にあり、ある程度掘削が進と、矢板が転倒する傾向が現れる。先程のすべり線と見比べてみると、根入れ部の破壊がこの傾向を増加させていることがわかる。同時に、掘削底面の変形もかなり大きくなっていく様子がよく現れている。
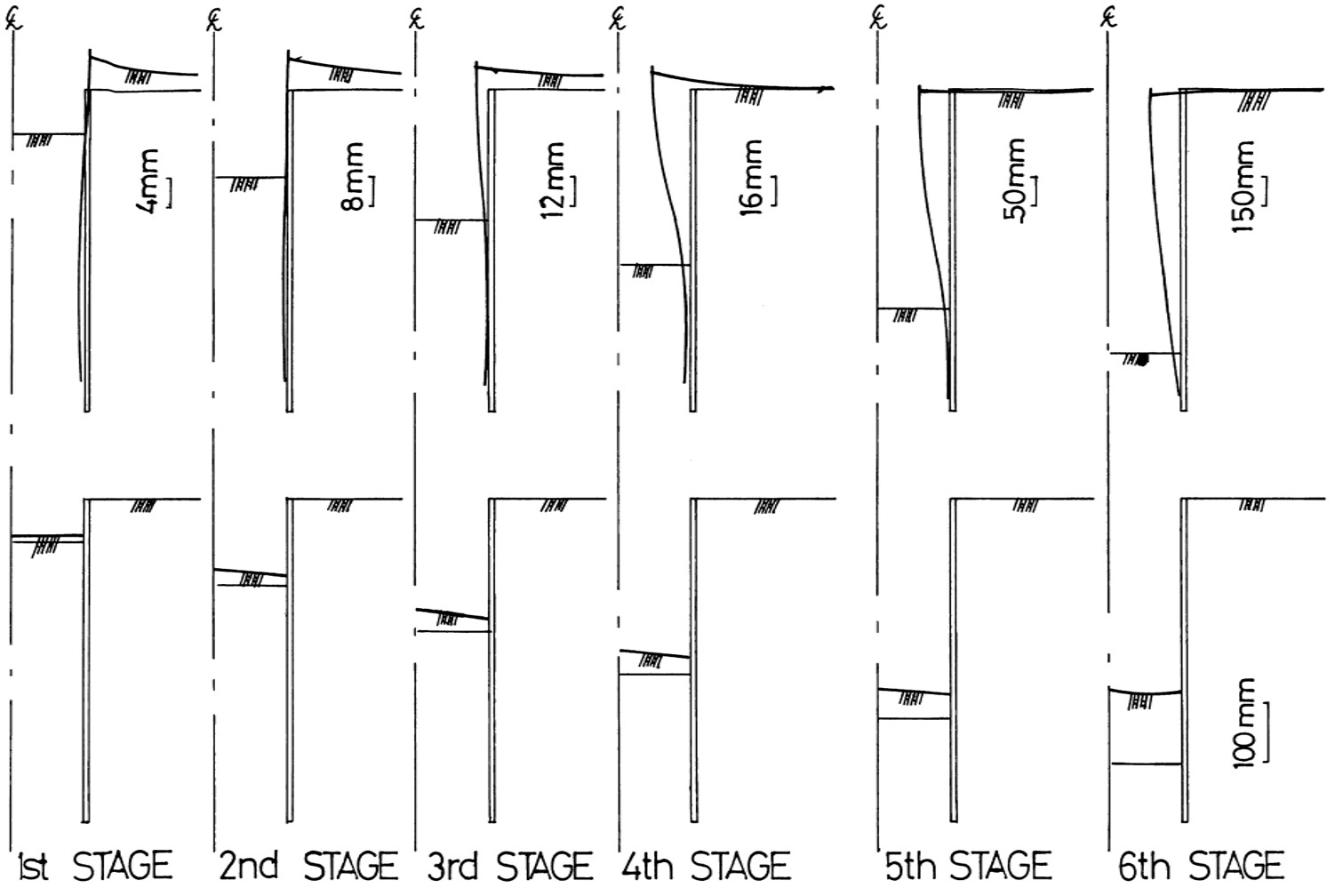
$\hspace{6em}$図6.15 自立式矢板のたわみと地盤の変形
図6.16は矢板の曲げモーメントを描いたものであり、掘削の進行とともに曲げモーメント分布も大きく変化している様子がうかがえる。弾性解析に比べるとこのモーメントは倍以上大きくなっており、塑性解析の必要性が理解できる。実際に、梁要素だけで解析する場合の土圧は塑性状態の力の釣合から求められたものが使われている。
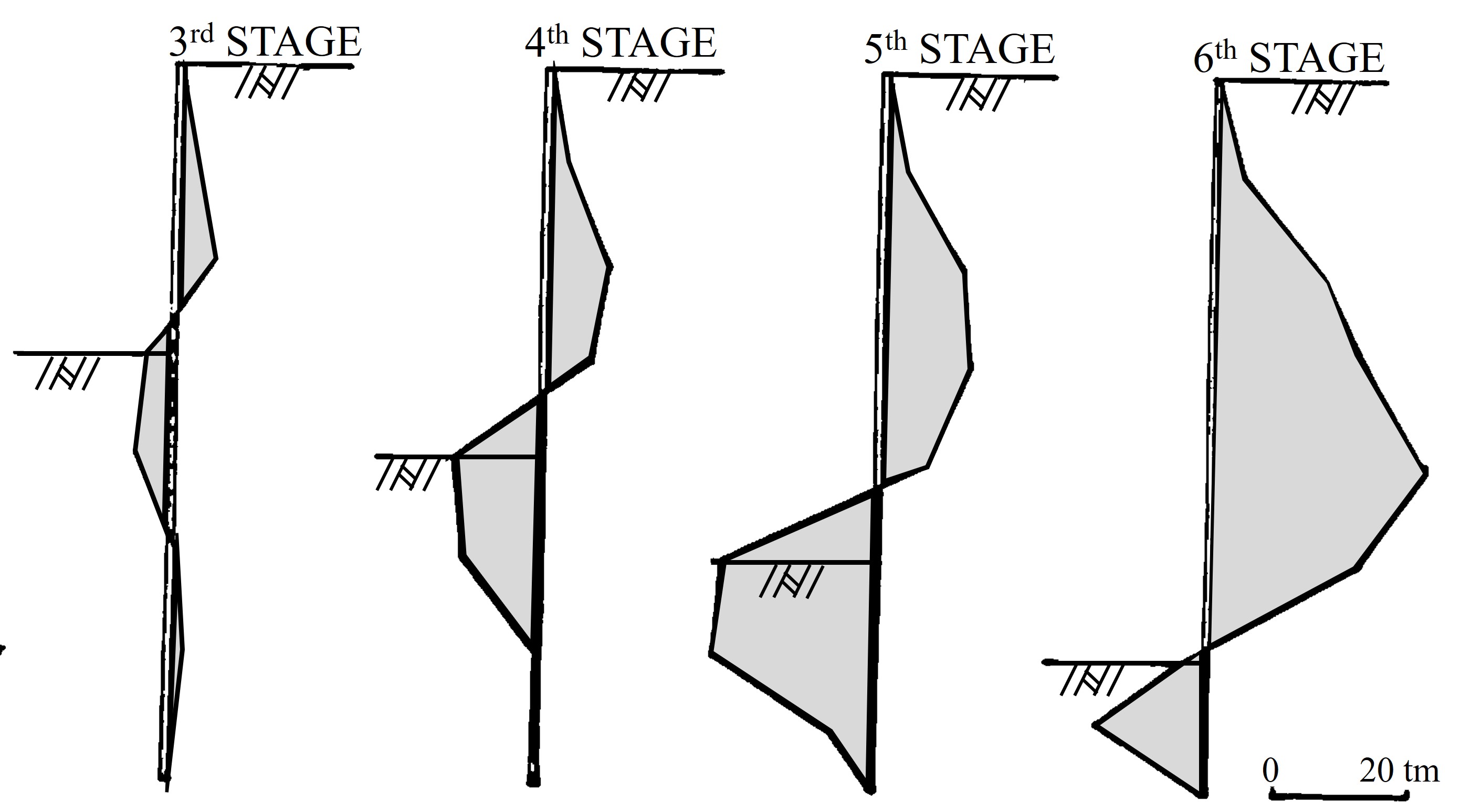
$\hspace{4em}$図6.16 自立式矢板の曲げモーメント
(2)切ばり式矢板の解析
次に切りばり式の土留め壁の解析例を示そう。切りばり式土留め壁の場合、掘削と切り梁の施工順序により得られる解が異なる。ここでの解析では時間による効果を無視しているため、厳密な意味での施工順序を考慮したことにはならない。しかし、各掘削段階で応力解放を行いながら切りばりを追加するため、掘削量に応じた解を得ることは可能であり、そのような意味で施工順序を考慮したことになる。
図6.17には本例題で行った解析手順が示されている。
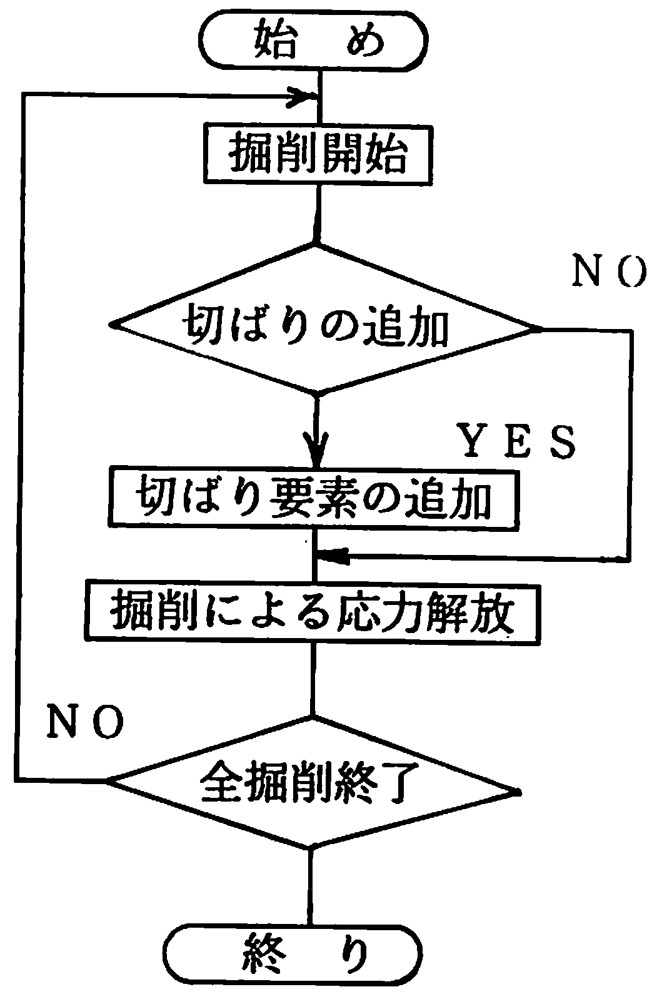
$\hspace{2em}$図6.17 解析手順
切りばりを表現する要素は矢板と同じ梁要素を用いる。ただし、軸力のみが作用し、曲げモーメントを受け持たない場合には回転ばねを0とする。また、切りばりは地盤の掘削後に追加するため、簡便的に
図6.18に示すよう、予め梁要素を地盤中に
図(a)ように取り込んでおき、掘削後、
図(b)のように梁要素どうしの結合部にばねを発生させる。このようにすると、掘削解放外力は矢板を通して切りばりに作用することになる。
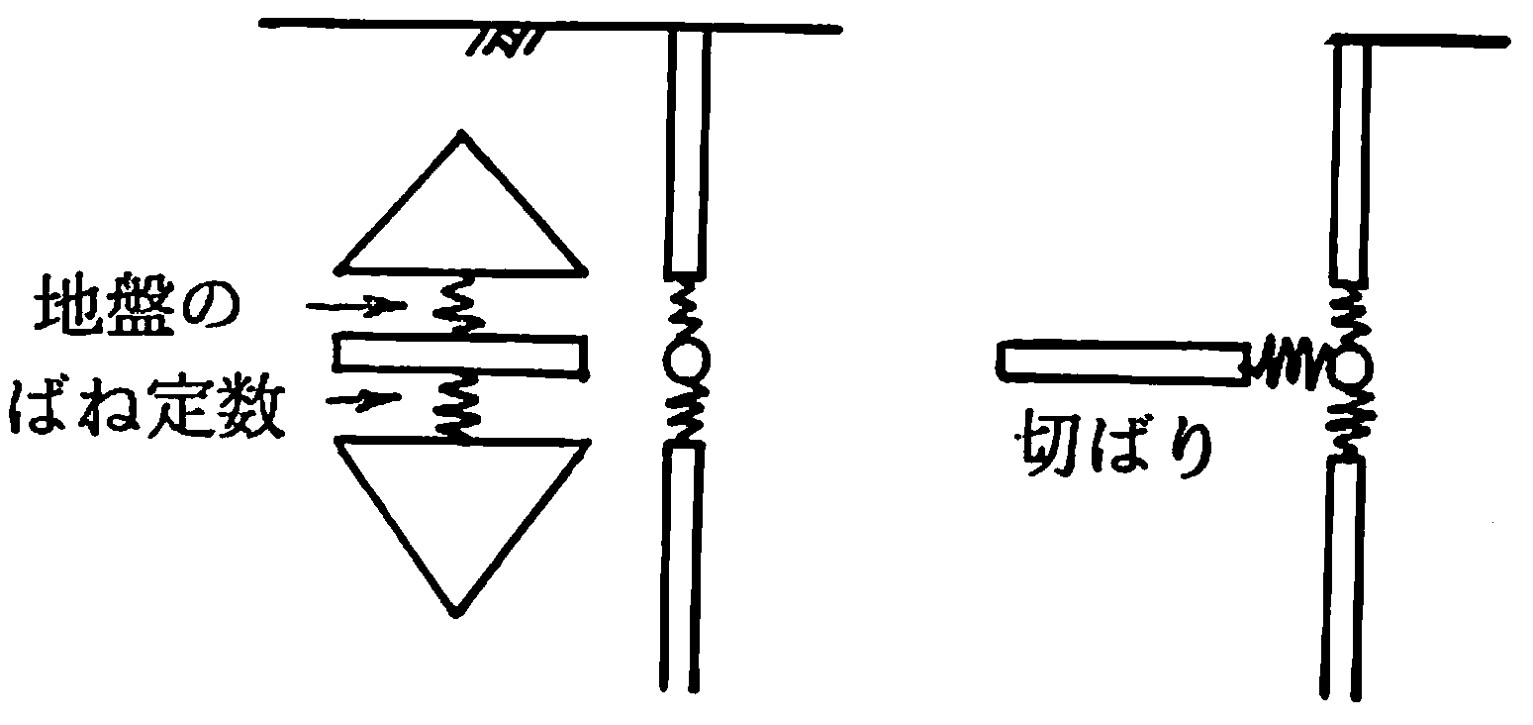
$\hspace{6em}$(a) 掘削前
$\hspace{4em}$(b) 掘削後
$\hspace{5em}$図6.18 切りばりのモデル化
以上のような解析手順により、
図6.19に示す簡単なモデルの解析を行てみよう。ここで、材料定数は図中に示す通りであり、矢板は弾性体と仮定する。また、境界条件は周辺スライドとする。
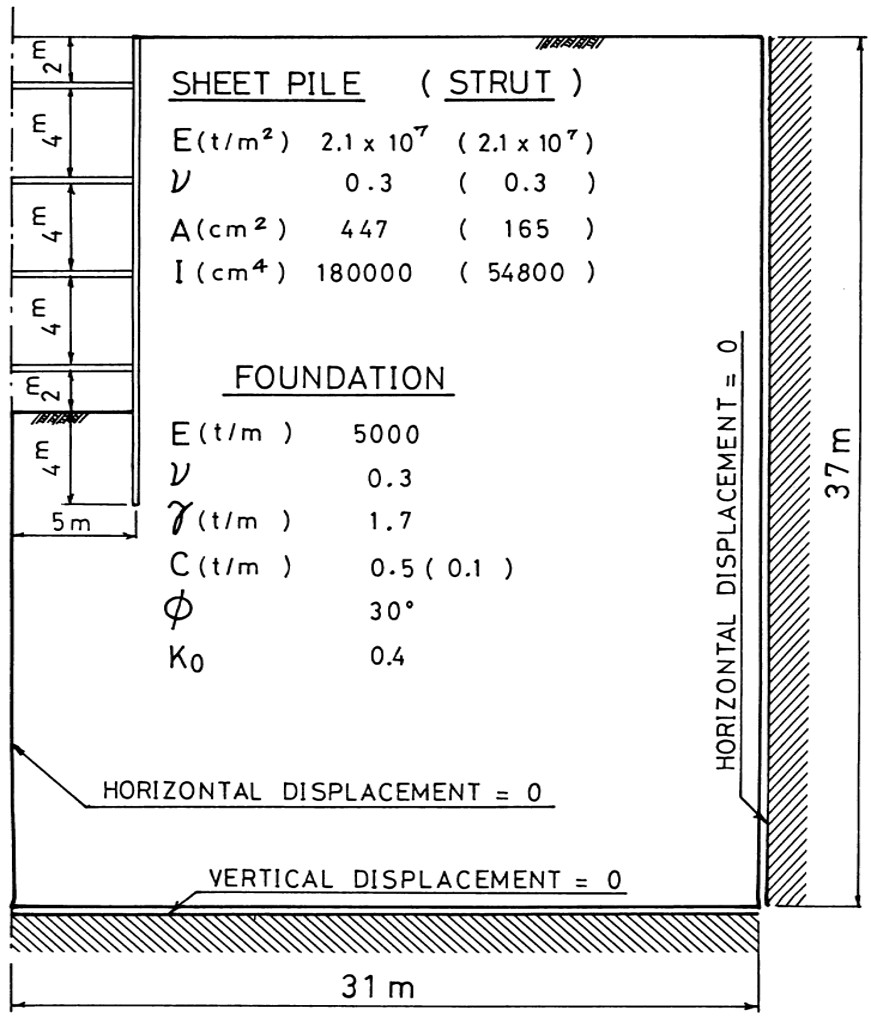
$\hspace{1em}$図6.19 切りばりの式矢板の解析モデル
図6.20は解析に用いた要素分割図が示されている。要素分割図ではよくわからないが、モデル図に描いてあったように矢板部分には梁要素が挿入されており、施工段階に従って切りばりを表現する梁要素が追加される。
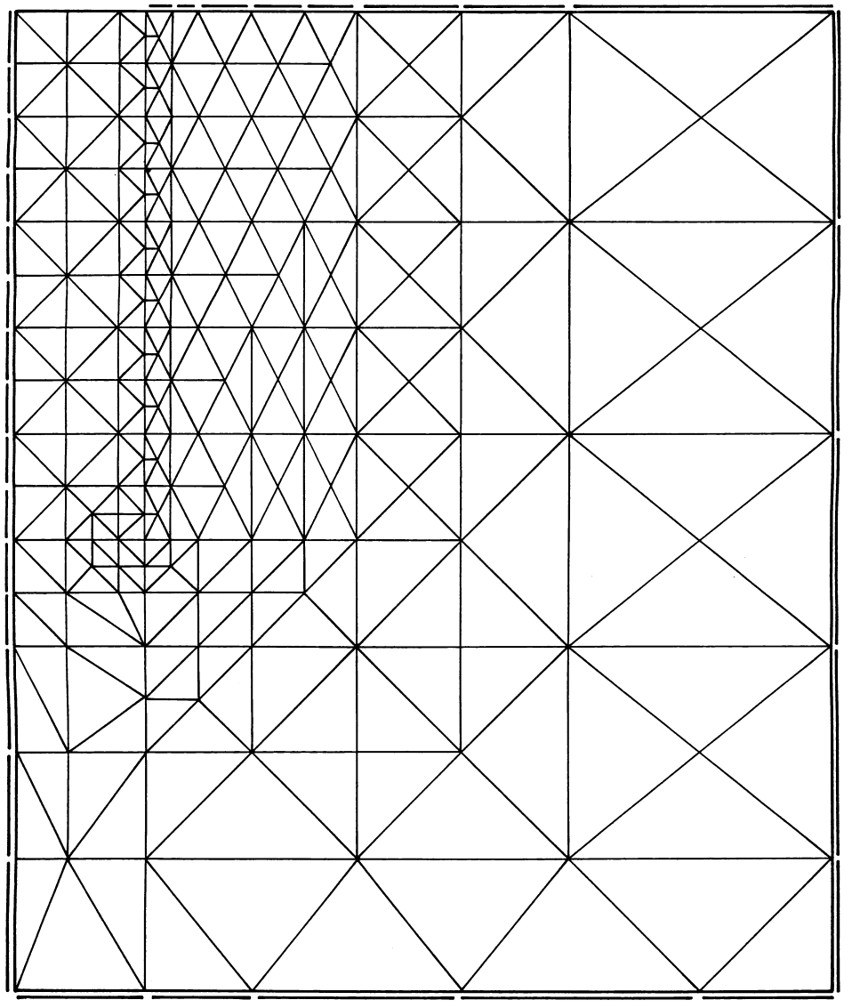
$\hspace{1em}$図6.20 切りばり式矢板の要素分割
図6.21は計算を行った掘削の順序と切りばりの追加状況を示したものである。掘削は$4 {\rm m}$ 毎に行われ、掘削を行った後、いったん応力解放が行なう。その後切りばりが追加され、次の掘削段階における解放力が発生したとき切りばりに軸力が生ずるものとしている。
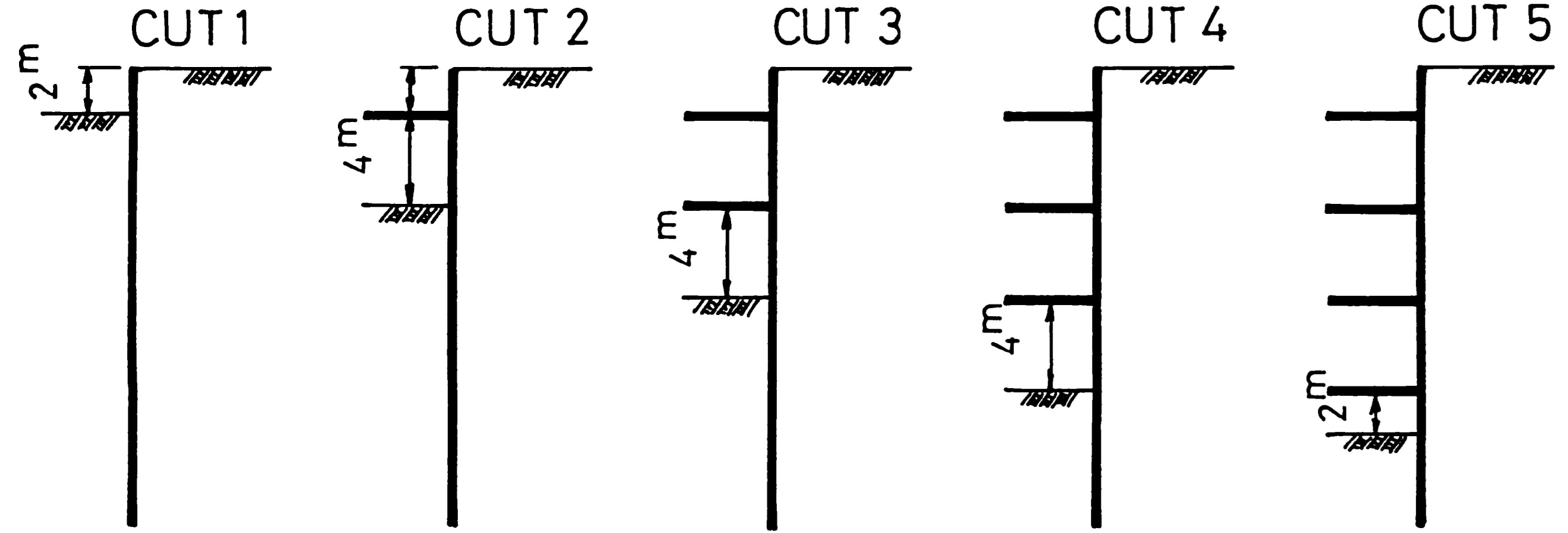
$\hspace{10em}$図6.21 施工順序
図6.22は離散化極限解析を行ったときの各掘削段階におけるすべり線パターンを示した図である。自立式矢板の場合と比べ、すべり線の発達領域は狭くなっている。
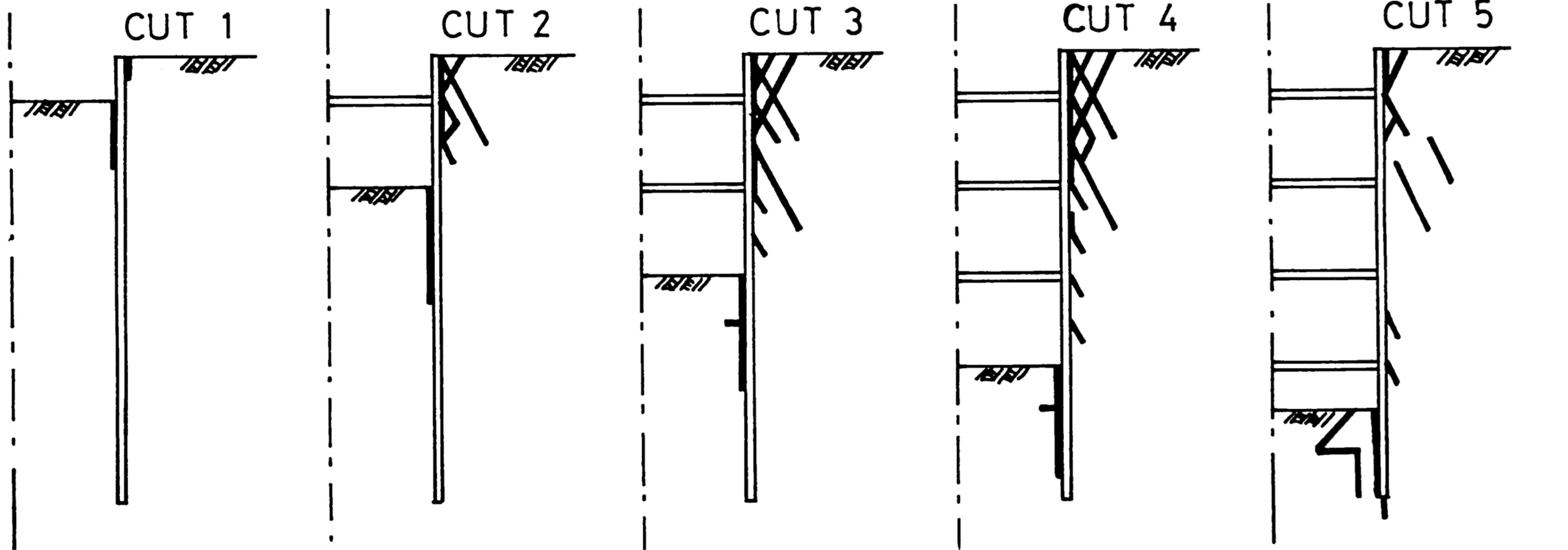
$\hspace{4em}$図6.22 各施工段階におけるすべり線
図6.23は最終掘削段階における矢板の曲げモーメントと切りばりの軸力、土圧分布を描いた図である。切りばりの影響で曲げモーメント分布も自立式矢板の場合と大きく異なっている。切りばりの軸力は図右側の四角で囲まれた部分に示されている。最下段の切りばり軸力の値が小さいのは最後の掘削量が少なかったためである。本計算では掘削と同時に解放外力をすべて作用させているが、実際には時間の経過とともに掘削解放外力が除々に作用するため、この結果のように最下段切りばりの軸力が小さくなるとは限らない。地盤反力を見ると受働側の反力が掘削底部で非常に大きくなっており、破壊の影響が現れている。
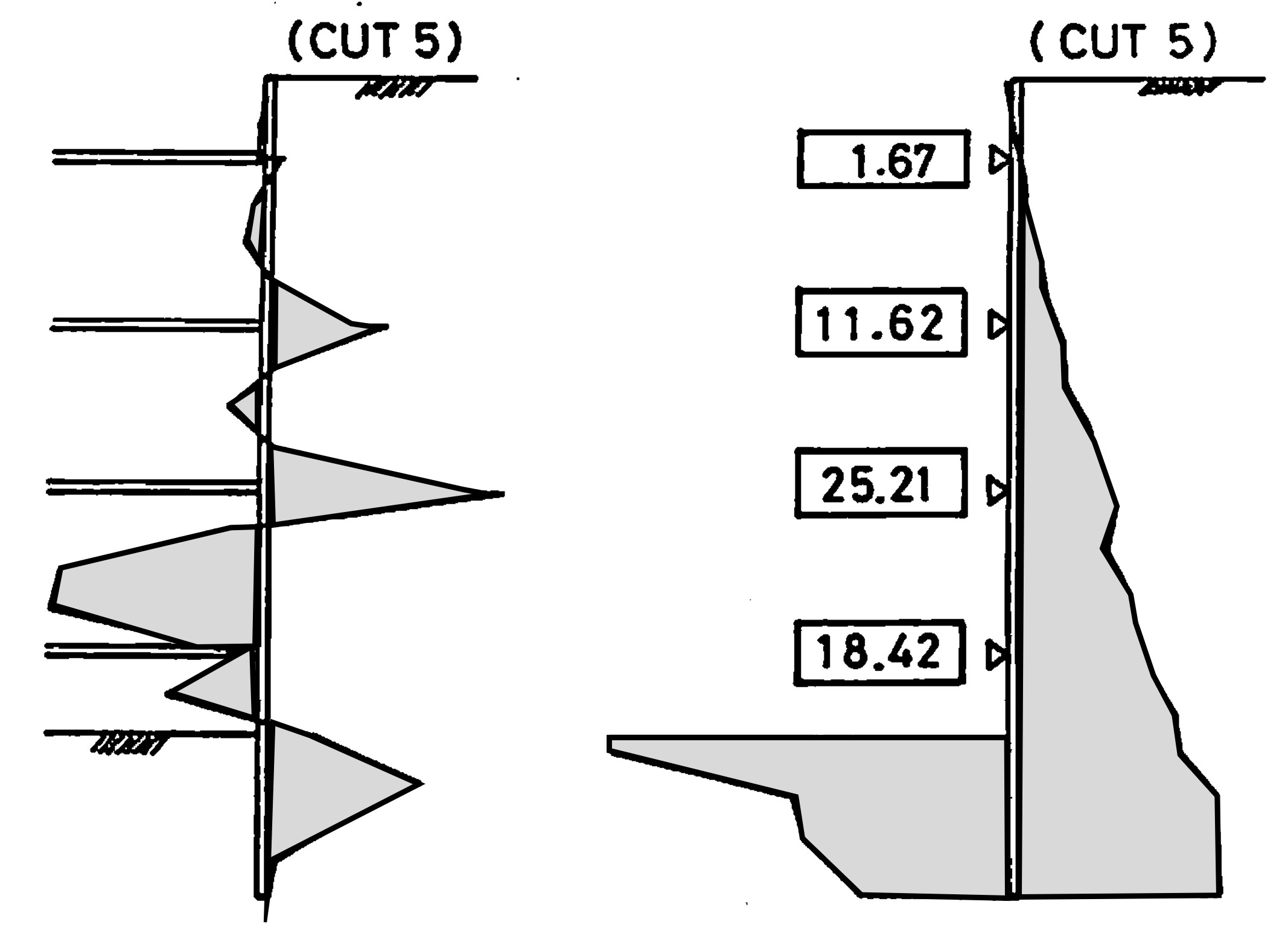
$\hspace{0em}$図6.23 切りばり式矢板の曲げモーメントと軸力、土圧分布
以上示したように、梁要素を利用することで自由度の変換を行うことなく、矢板などの薄いたわみ性土留め壁のような変形が破壊に影響する問題に対しても離散化極限解析が行えることが理解できた思う。ただし、厳密な意味での施工段階を考慮するなら、粘塑性などの時間効果を導入する必要があろう。
トンネルは他の地中構造物に比べ、比較的深いところに施工されるケースが多いが、近年の都市に施工されるトンネルは比較的浅い場所に施工されるケースも見受けられる。また、山岳トンネルのような場合でもトンネル孔口付近は土被りが浅く危険が伴う。トンネルの問題はそれ自身の問題はもちろんのこと、トンネル付近に埋設されている地中構造物に対する影響や、トンネルを含む地盤全体の安定性に対する検討も重要な課題となる。本節では、このようなトンネルに関係する問題の離散化極限解析について解説する。
トンネル掘削後の応力解析法には有孔板理論による解析法、応力解放による解析法、直接載荷による解析法などがある。簡便的に解析を行う場合、
図6.24(a)に示すよう、予めトンネルに該当する部分を空洞にし、地山の自重や他の外力を荷重として解析する直接載荷による解析法が利用されている。
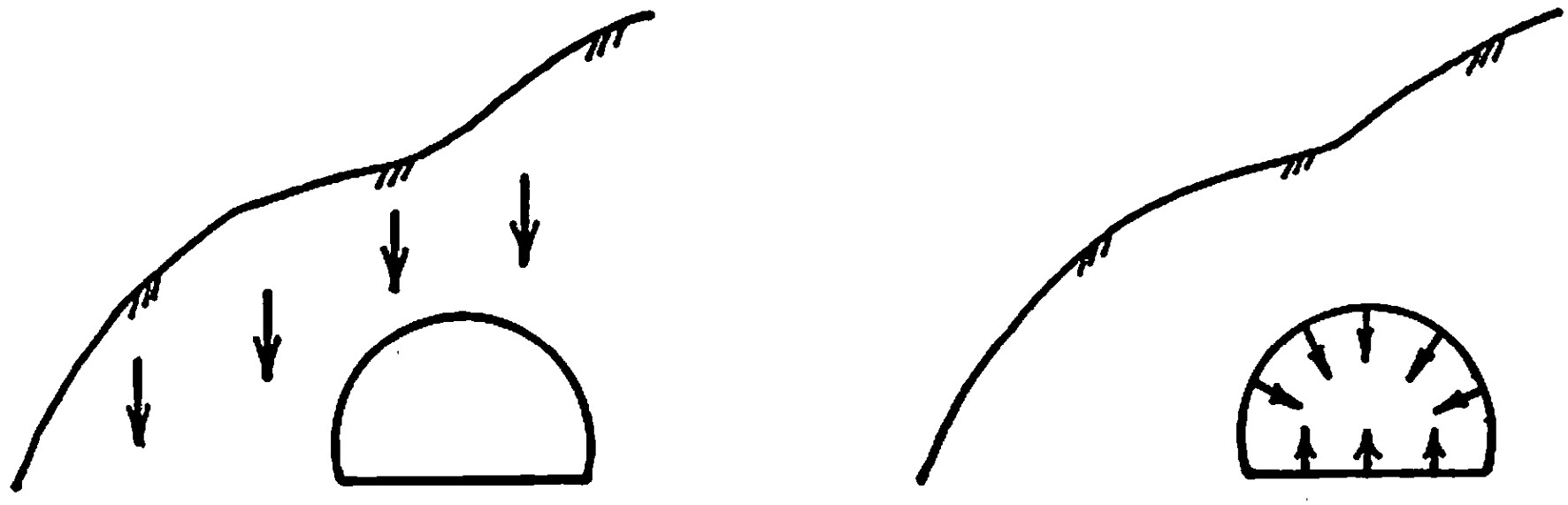
$\hspace{0em}$(a) 直接載荷による解析法
$\hspace{1em}$(b) 解放力による解析法
$\hspace{6em}$図6.24 トンネル応力解析法
一方、覆工の打設時期など施工段階を考慮する場合には、
図6.24(b)に示すような応力解放による解析法がよく用いられている。実際に計算を行ってみると施工段階を考慮した逐次掘削工法の方が全断面掘削より安全であり、詳細な解析を行いたいならば施工段階を考慮した応力解放による解析法が適していよう。ただし、掘削に伴う解放力が一度に作用するということは現実的ではなく、たわみ性土留め壁の場合と同様、厳密な意味での応力解放を取り扱うためには粘塑性などの時間の効果を導入する必要がある。
トンネルの安全性を検討する場合、施工途中の素堀の状態と同時に、支保工や覆工を建て込んだ場合の解析も必要である。覆工などのようにある程度厚みがある場合には、平面要素を用いてモデル化することもあるが、支保工のように地山全体から眺めると比較的薄い材料の場合、梁要素によるモデル化が行われる。川井モデルにおけるモデル化の場合、
図6.25のように梁要素とピン要素により支保工を表現し、梁要素に隣接する平面要素との間のばねとして平面要素のばねを設定する。
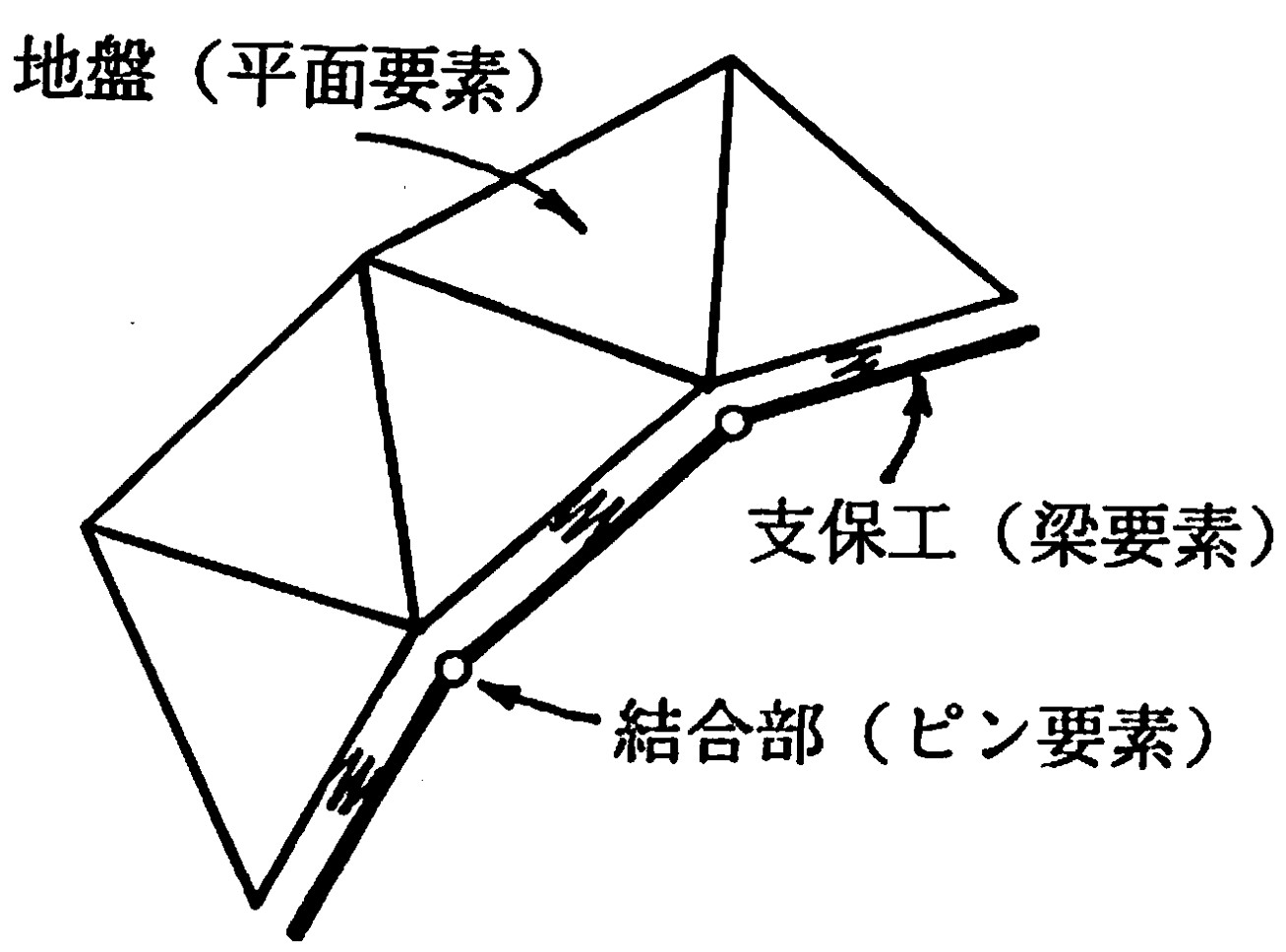
$\hspace{2em}$図6.25 支保工のモデル化
もし、掘削による解放力を用いて計算する場合には、初めに、
図6.26(a)に示すよう予め梁要素を挿入し、梁要素と平面要素の間のばねに地盤のばね定数を用い解析する。このとき、梁要素どうしは結合されていないものとする。次に、掘削後、
図(b)に示すよう、ピン要素を追加して梁要素を結合すれば、骨組構造が形成され、その効果を計算に追加することができる。
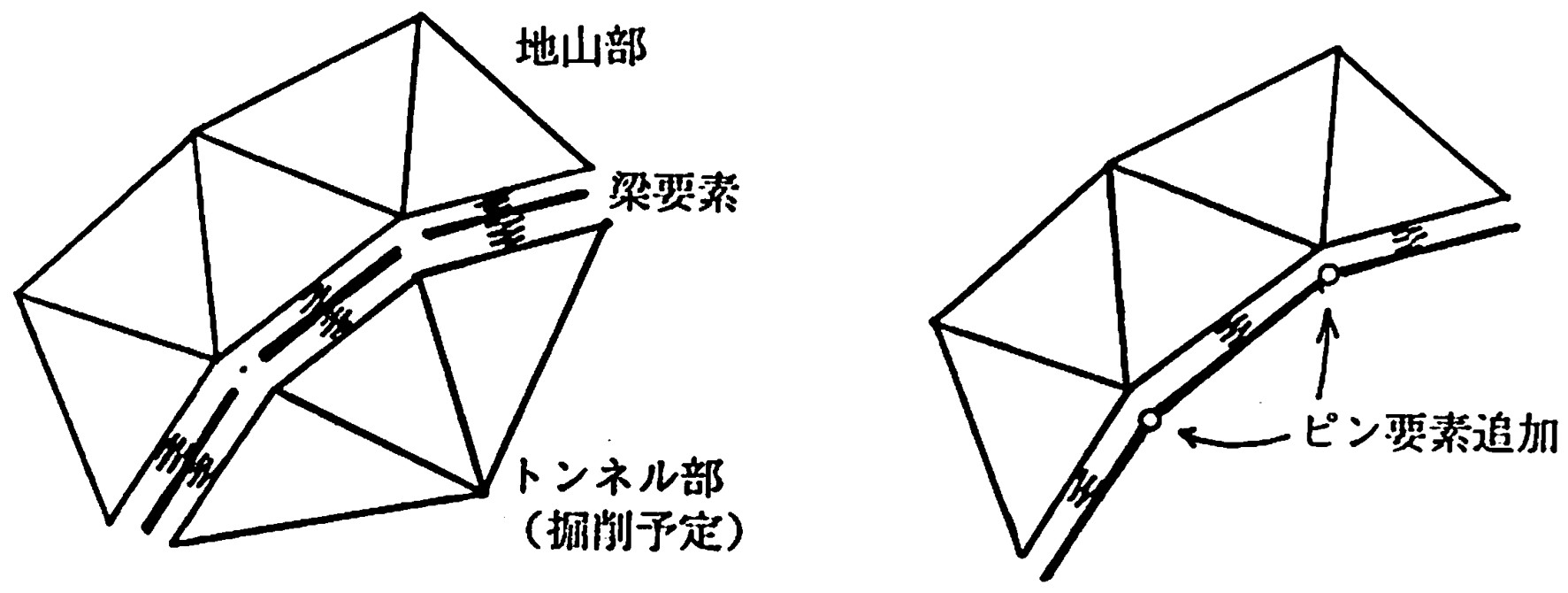
$\hspace{4em}$(a) 掘削前
$\hspace{9em}$(b) 掘削後
$\hspace{4em}$図6.26 掘削に伴う支保工のモデル化
ロックボルトのモデル化の場合、
図6.27に示すよう、梁要素を用いる。ただし、ロックボルを表現する梁要素と地盤に関する平面要素の間のばねは図に示すように設定しな ければならない。また、一般にロックボルトは軸力のみを受け持つものとすることが多く、この場合には回転ばねを無視し、軸力のみが作用するトラス要素にする必要がある。
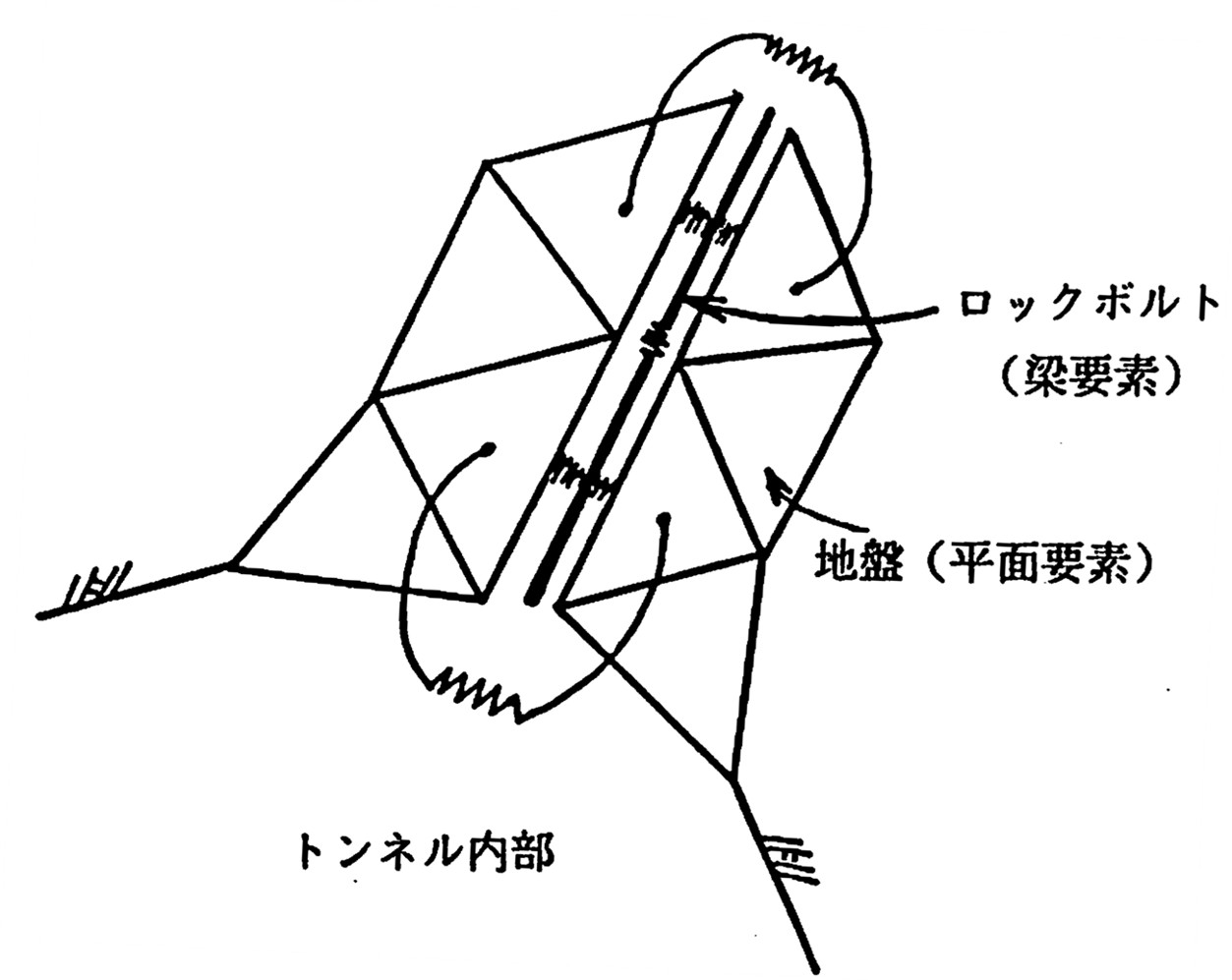
$\hspace{0em}$図6.27 ロックボルトのモデル化
以下にトンネルに関する簡単な解析例を2例示そう。
(1)帯状の落とし戸に加わる土圧
Terzaghiは砂質地盤からなる地山のトンネル土圧を乾燥砂を用いた帯状の落とし戸実験から推論した。
図6.28は $D$ の深さを持つ箱に乾燥砂を入れたモデルで、その底に幅 $B (ab)$ の落とし戸が設置されている。実験では落とし戸を $\delta$ だけ降下させ、そのときの落とし戸に加わる土圧 $(p)$ を計測している。$\delta=0$ のとき土圧は $p=\gamma D$($\gamma$:土の単位体積重量)となるが、$\delta$ が増加すると $p$ は急減し、ある最小値をとった後、若干増加し一定値に近づくが、この戸に隣接している台の部分に加わる土圧は増加すると述べている。
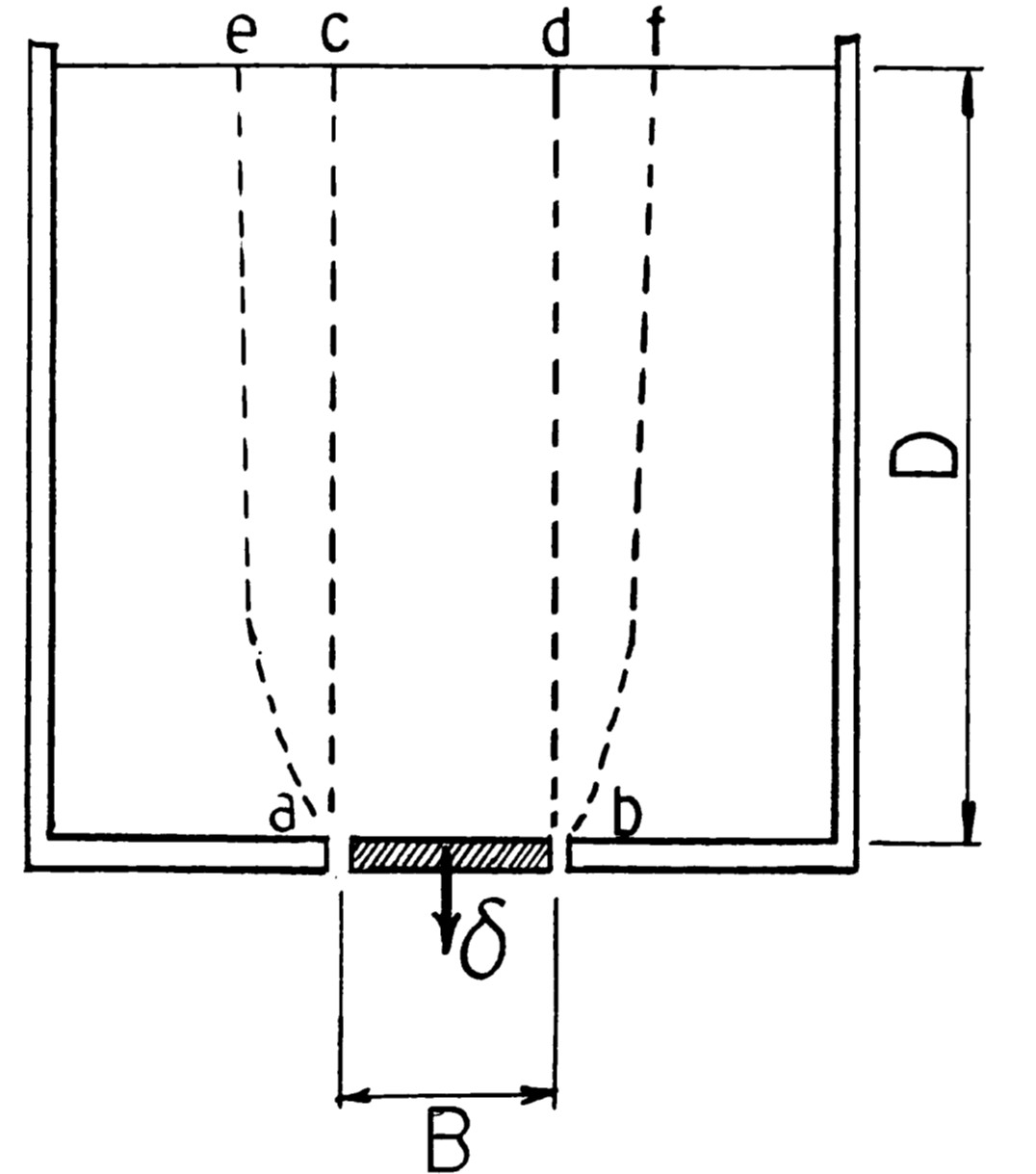
$\hspace{0em}$図6.28 落とし戸の解析モデル
これは、
図6.29に示すよう、落とし戸の上にある砂柱の沈下がその砂中の側面 $ac$ と $bd$ に沿って生ずるせん断応力によって抵抗されるためであると思われる。そこで、ここではこの落とし戸の問題を川井モデルにより解いてみる。
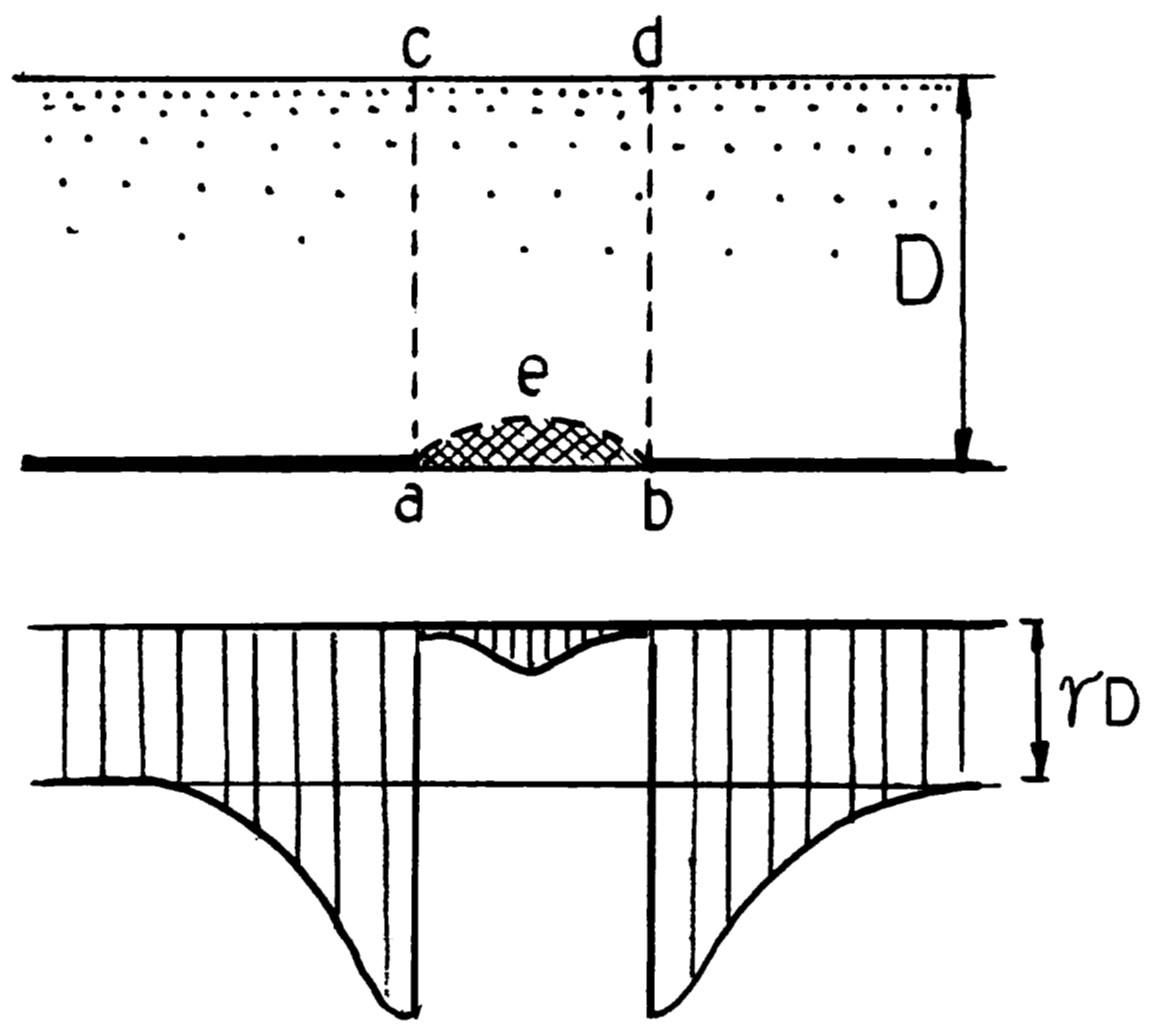
$\hspace{1em}$図6.29 落とし戸近傍の土圧分布
図6.30に計算に用いたモデルと要素分割図が示されている。図中の $K_0$ は静止土圧係数である。これを用いて初期土圧を仮定し各ばねに初期値として与え、その後、落とし戸を降下させることにより計算を進めた。深さについては、$8 {\rm m}、12 {\rm m}、$ $16 {\rm m}、20 {\rm m}$ の4通り仮定しており、比較的浅い場合に該当する。
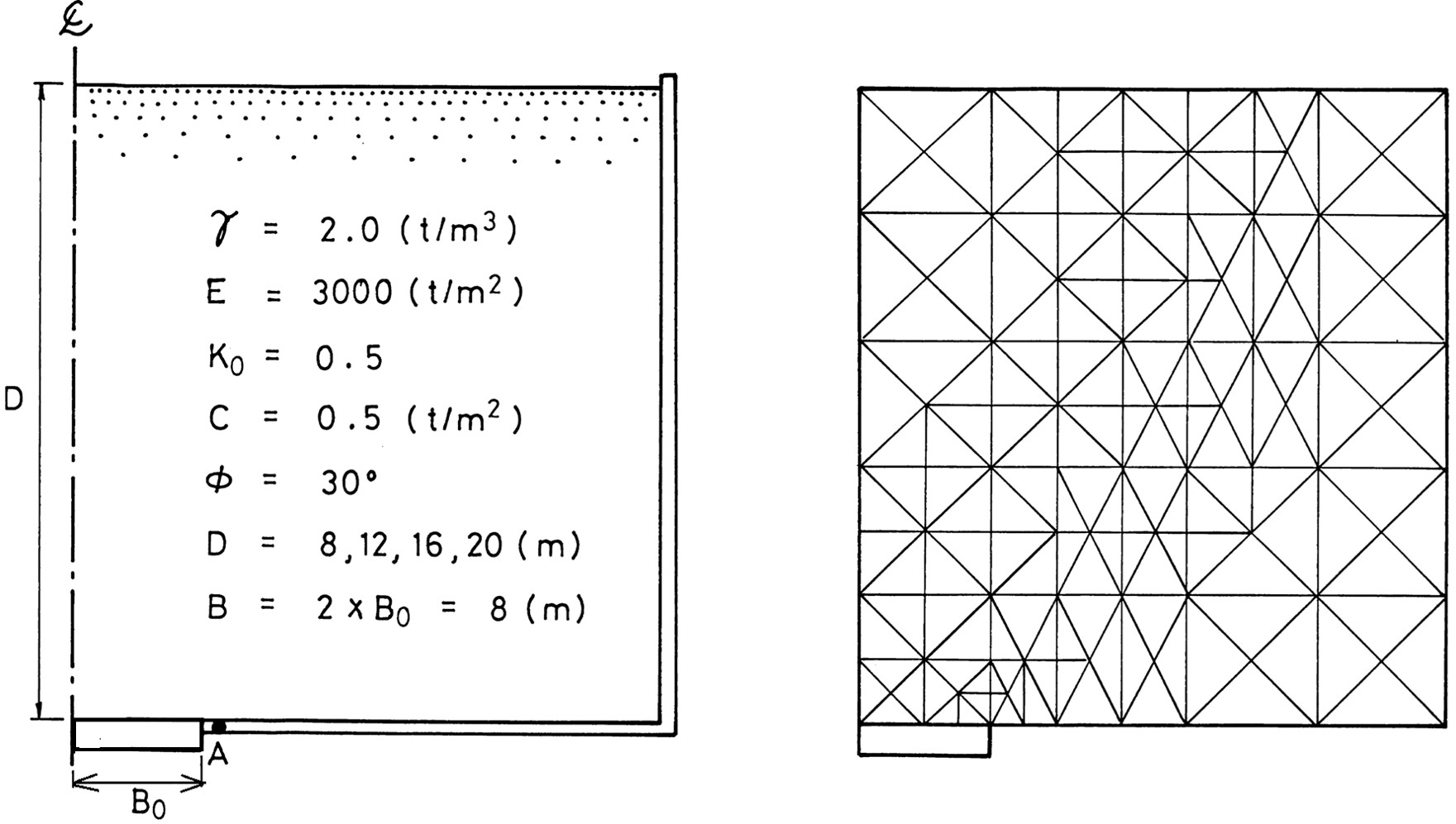 $\hspace{4em}$(a) 解析モデル
$\hspace{8em}$(b) 要素分割
$\hspace{4em}$(a) 解析モデル
$\hspace{8em}$(b) 要素分割
$\hspace{1em}$図6.30 落とし戸の計算に用いたモデルと要素分割
図6.31には $2D/B$ が3と5の2ケースのすべり線が示されている。$2D/B=3$ の浅いケースでは落とし戸上の鉛直方向のすべり線により崩壊しているが、$2D/B=5$ の場合には若干膨らみをもってすべりが発生している。このケースは浅い場合と深い場合の境目の深さでありTerzaghiの議論と一致している。
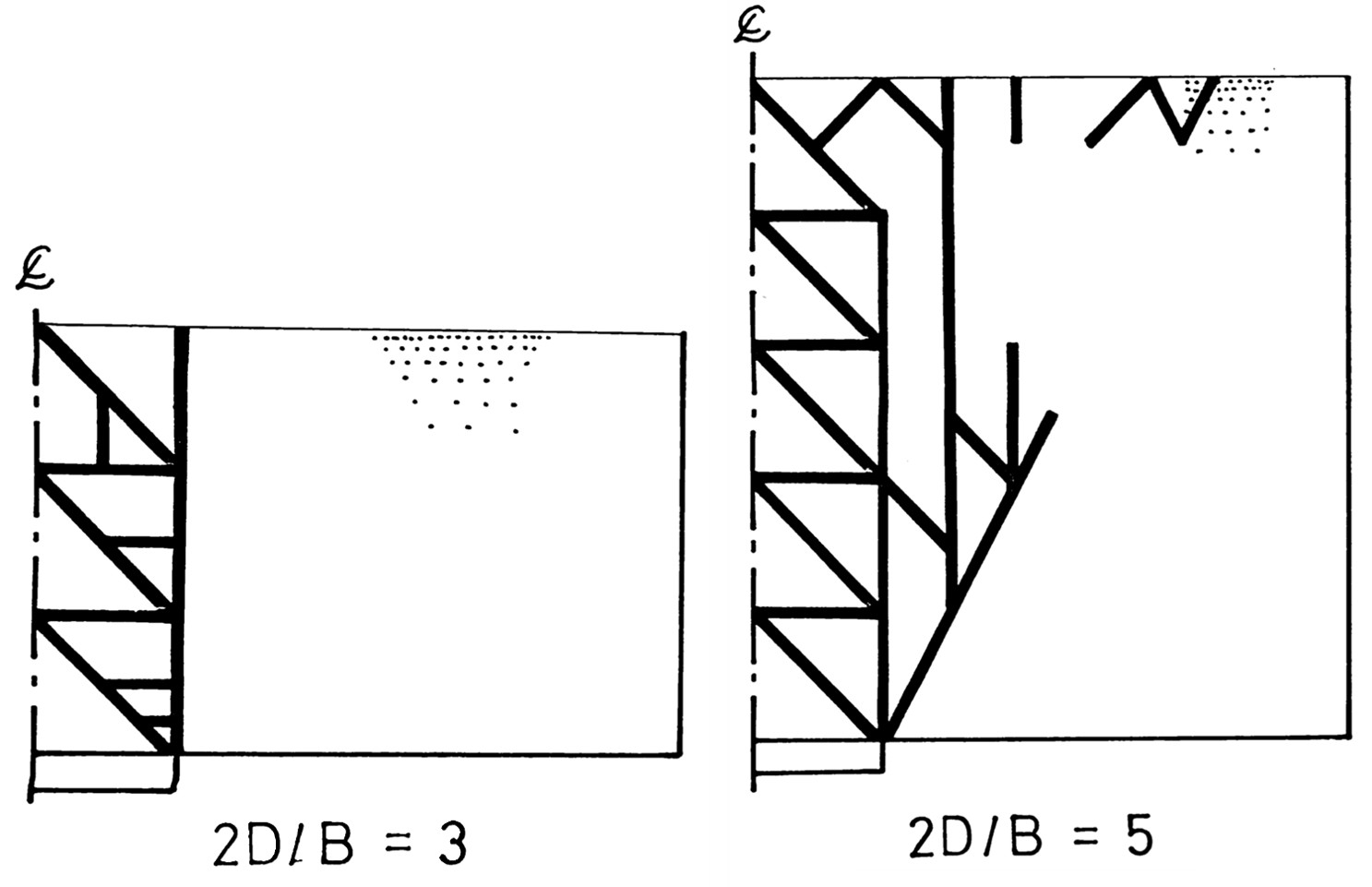
$\hspace{4em}$図6.31 すべり線発達状況
図6.32は落とし戸の降下量を横軸に、また、箱の底部ににおける土圧を縦軸にとりプロットしたものである。ただし、
図(a)の落とし戸に加わる土圧は落とし戸面における平均値であり、
図(b)に示す落とし戸近傍の点は
図6.30に示した $A$ 点である。落とし戸上の土圧は降下量の増加とともに一定値に近づく。一方、近傍の点 $A$ では降下量の増加とともに土圧も増加するが一定量を越えると逆に減少する傾向が現れる。これは、落とし戸の降下とともに回りの地盤も摩擦により沈降し、限界に達するとすべりが発生し、応力解放が発生するためである。
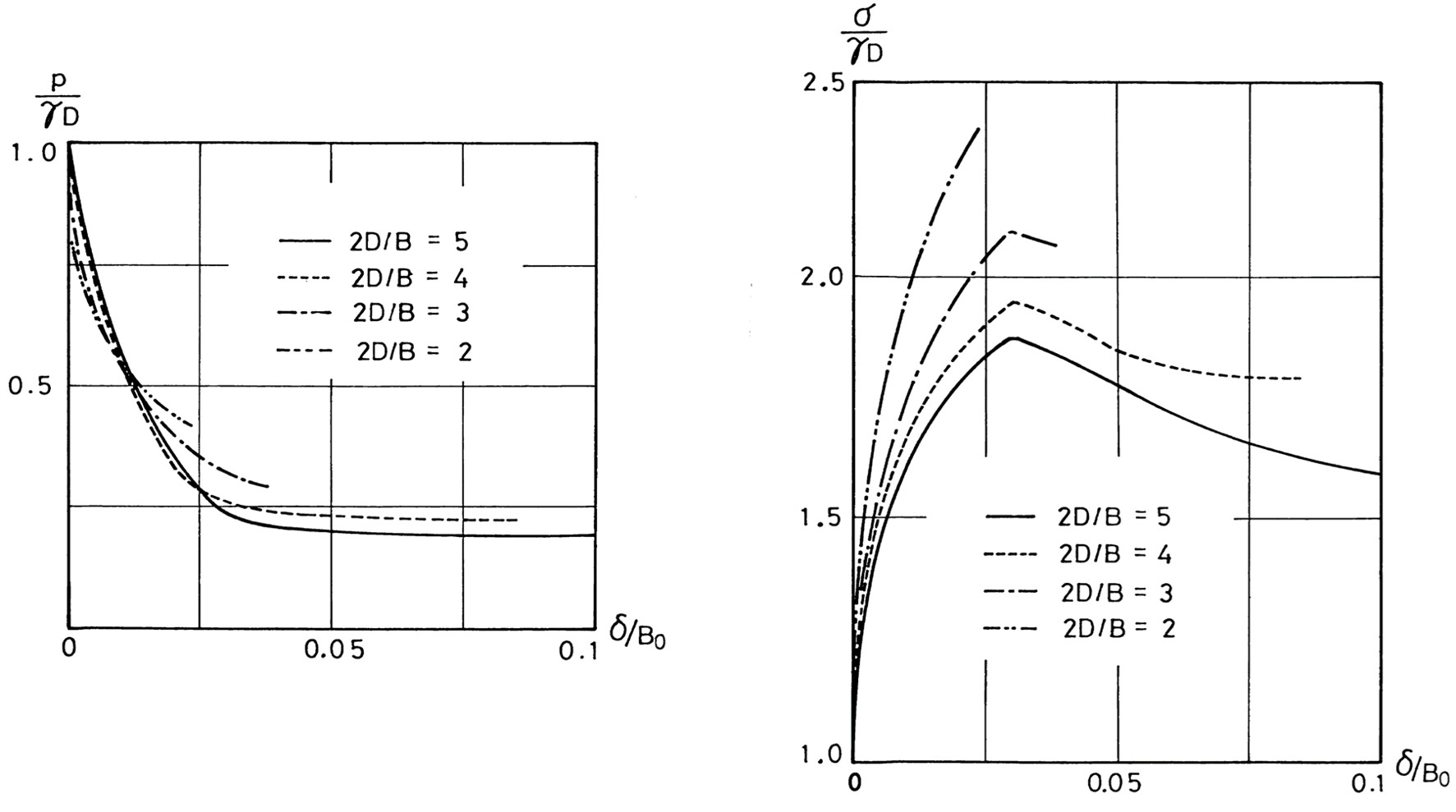
$\hspace{3em}$(a) 落とし戸上
$\hspace{5em}$(b) 落とし戸近傍(A点)
$\hspace{5em}$図6.32 落とし戸の降下量と土圧の関係
次に、それぞれのケースについて、箱の底部における鉛直土圧をプロットしてみた結果を
図6.33に示す。実線は落とし戸の近傍 $A$ 点における土圧が最大値をとったときの土圧分布であり、点線は最終的に崩壊する直前の土圧分布である。土被りが深いほど両者の差は大きくなり、$2D/B=5$ では大きく異なっている。これは、土被りが浅いほど応力解放が進む以前に崩壊が発生するためである。
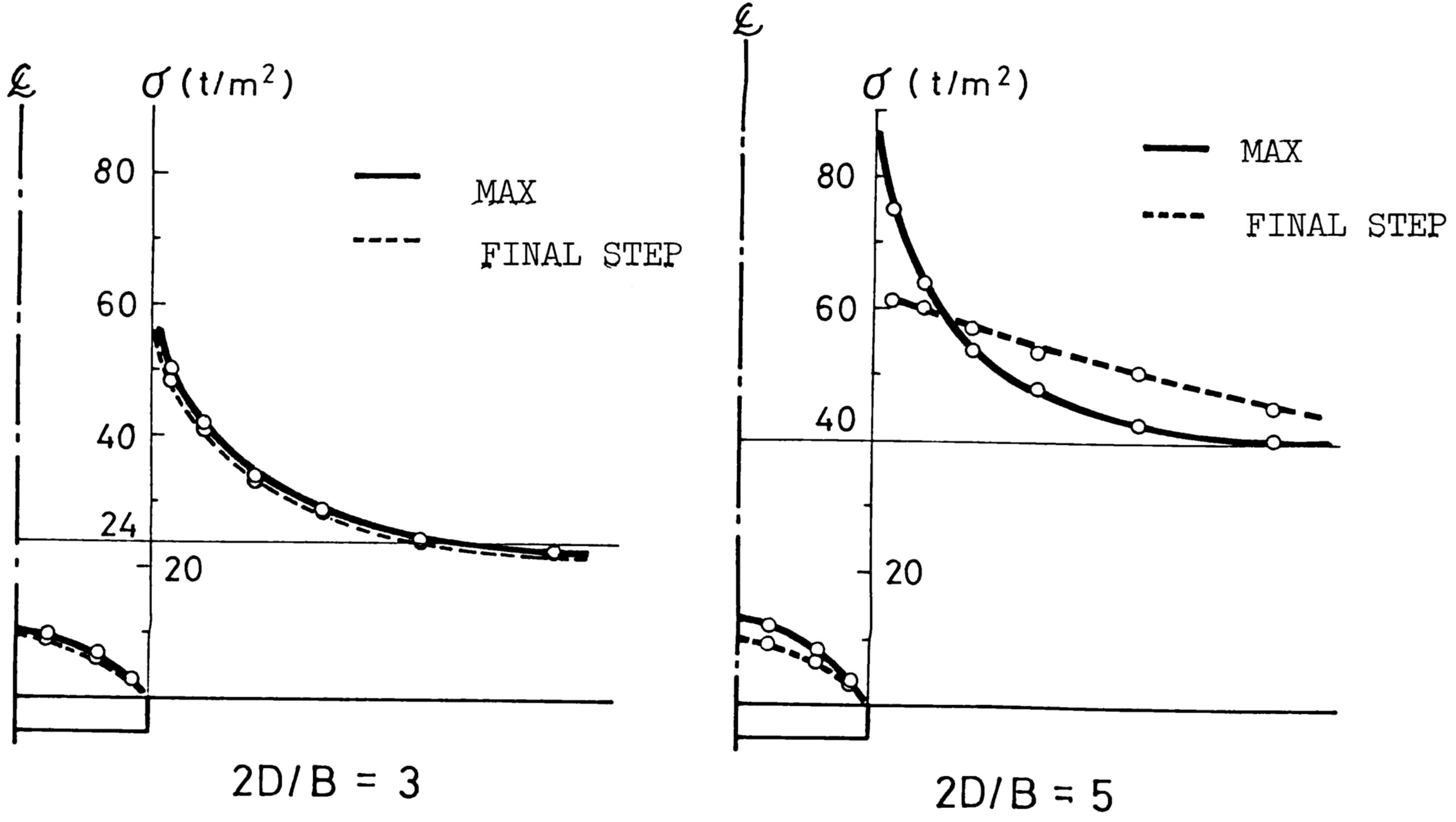
$\hspace{6em}$図6.33 箱底部の垂直土圧
(2)斜面近傍のトンネル安定解析
土被りの浅いトンネル坑口付近は事故の危険が高く、掘削に伴う斜面の安定性やトンネルへの影響などを予め解析しておくことが大切である。ここでは、このような土被りの浅い斜面近傍のトンネルを例にとり解析した結果を示そう。
図6.34に解析に用いたモデル図を示す。図中のCは安定した基礎地盤、Bは軟弱地盤、Aは盛土地盤であり、それぞれの材料定数
表6.1に示す。境界条件は周辺スライドで、解析は直接載荷による解析法を用いた。
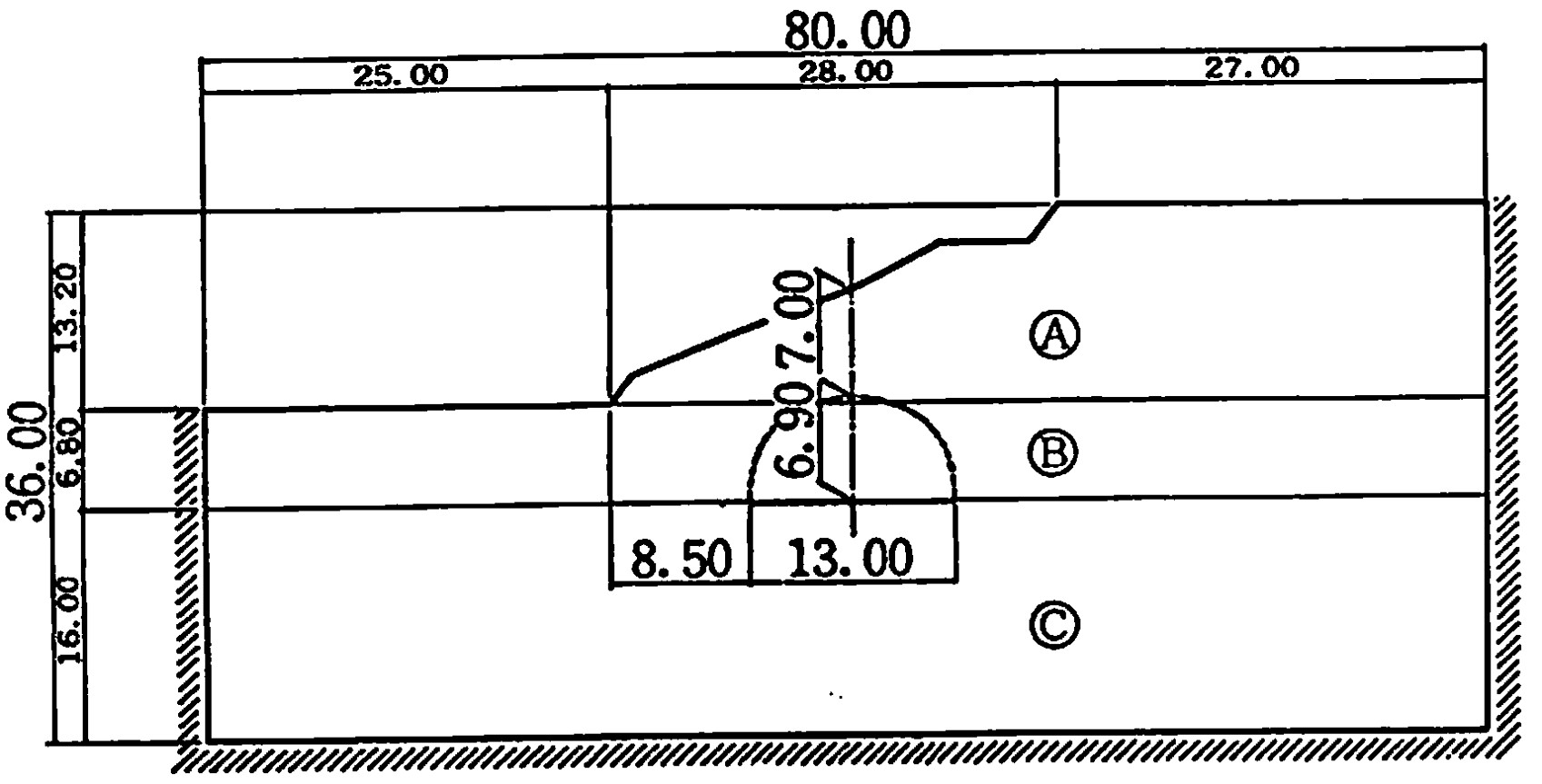
$\hspace{5em}$図6.34 斜面近傍のトンネルモデル
表6.1 再計算に用いた材料定数
| 材料定数 |
単 位 |
A |
B |
A |
| 弾性係数 |
${\rm t/m^2}$ |
3000 |
3500 |
8000 |
| ポアソン比 |
- |
0.4 |
0.35 |
0.3 |
| 粘着力 |
${\rm t/m^2}$ |
4.0 |
5.0 |
3.0 |
| 単位体積重量 |
${\rm t/m^3}$ |
1.8 |
1.6 |
1.8 |
| 内部摩擦角 |
${\rm deg}$ |
0.0 |
0.0 |
40.0 |
計算ケースとしてトンネル掘削前の盛土斜面安定解析、素堀トンネル掘削に伴う斜面の安定解析、さらに支保工が建て込まれた状態の安定解析の3ケースを考えた。支保工としては200Hの鋼材を1m間隔で用いている。
図6.35には解析に用いた要素分割図が示されている。
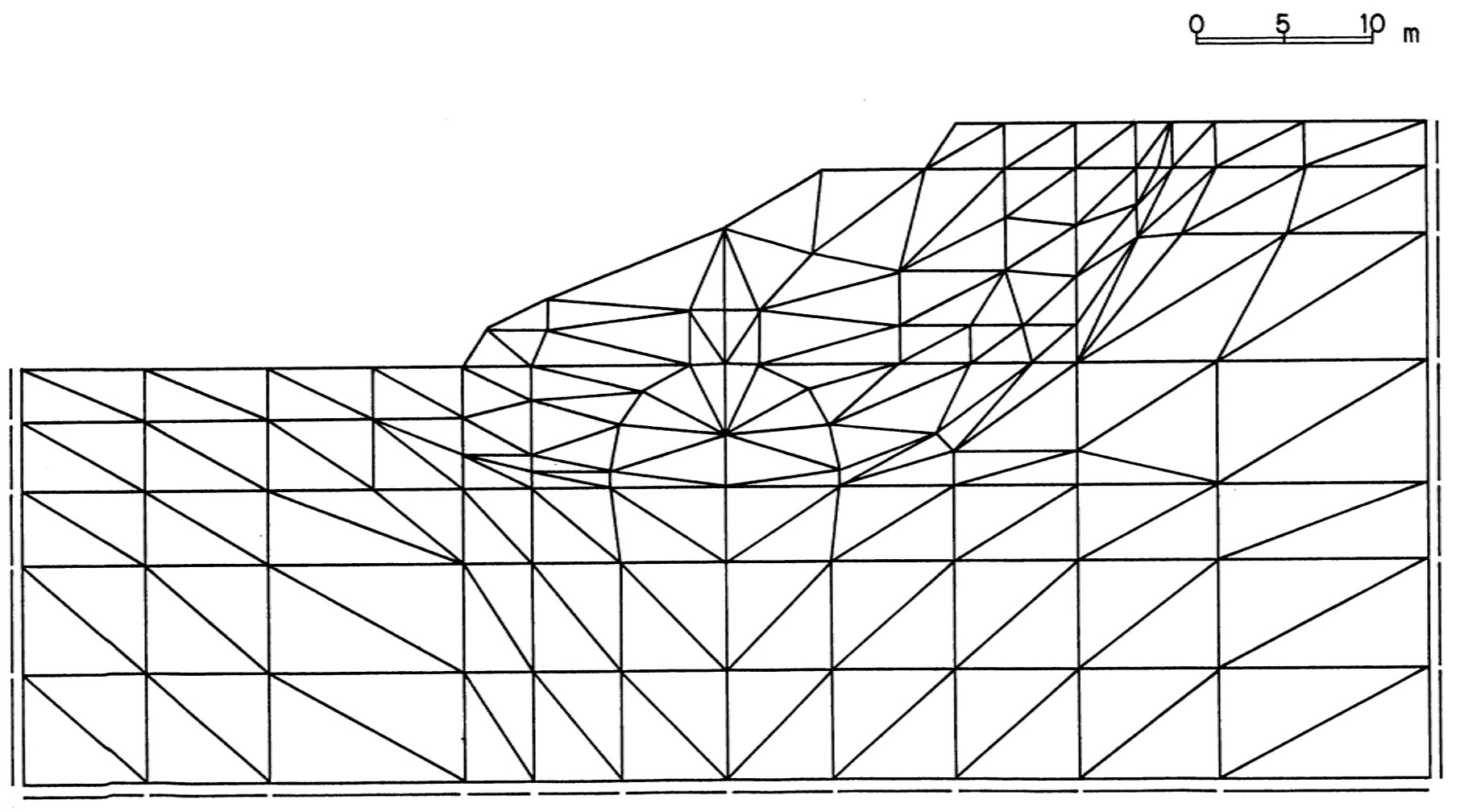
$\hspace{8em}$図6.35 要素分割
図6.36にトンネル掘削前の盛土斜面に関する安定解析結果が示されている。すべり線をながめると、軟弱地盤層Bで破壊が進行するものの盛土層と基礎地盤ではすべり線が発達せず、斜面全体としては安定を保っている。また、変位モードをながめても斜面上部の陥没あるいは法面のはらみ出しはみられない。
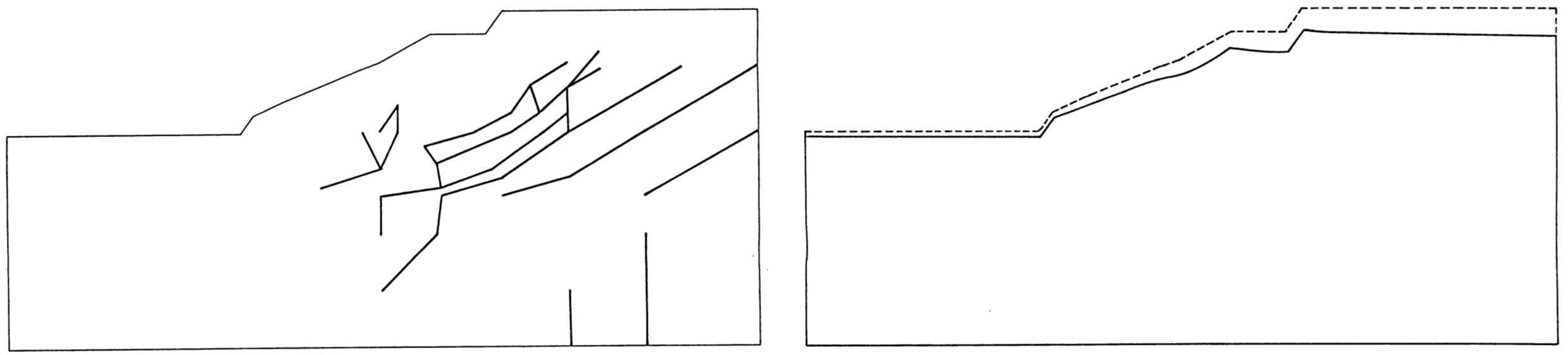
$\hspace{6em}$(a) すべり線
$\hspace{8em}$(b) 変位モード
$\hspace{10em}$図6.36 盛土斜面の安定解析結果
次に素堀トンネルの例を
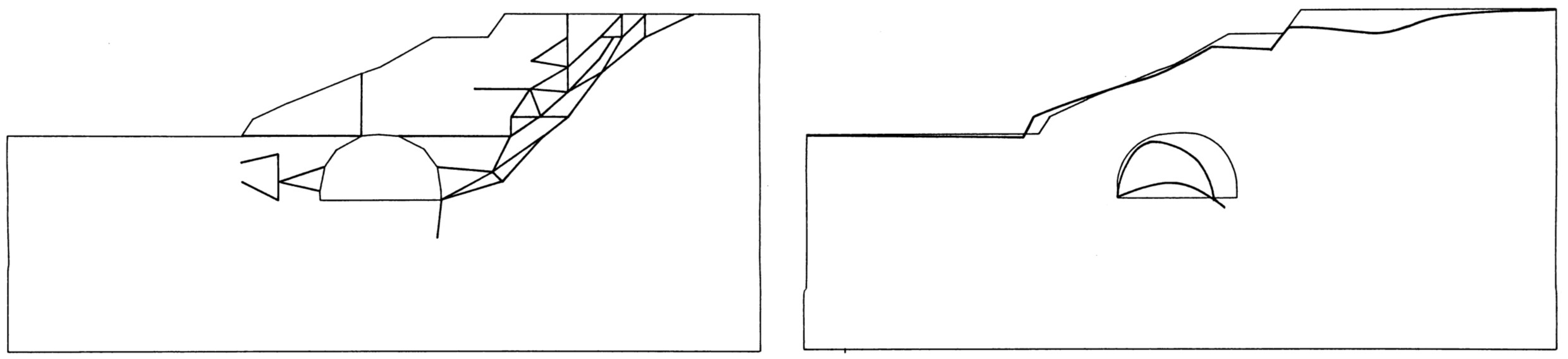
図6.37に示す。この解析には直接載荷による解析法を用いている。図は自重載荷率35%の場合で、このときトンネルは崩壊する。すべり線の発達状況をながめると、盛土安定解析では見られなかったすべり線がトンネルに向かって発生している。変位モードより、このすべりの発生によりトンネルが押しつぶされる傾向が伺える。
$\hspace{6em}$(a) すべり線
$\hspace{8em}$(b) 変位モード
$\hspace{10em}$図6.37 素掘りトンネルの安定解析結果
このことを、さらに詳しく見るため、トンネル周辺の水平変位を横軸にとり、縦軸に自重載荷率をとってプロットした結果が
図6.38である。C点ではほとんど水平変位が発生していないにもかかわらず、A点、B点では自重載荷率30%を越えたあたりから急激に変形が増大している様子が現れている。このことから、本来安定であった斜面がトンネルを掘削することにより、その中へ落ち込むように斜面にすべりが発生するということが理解できる。
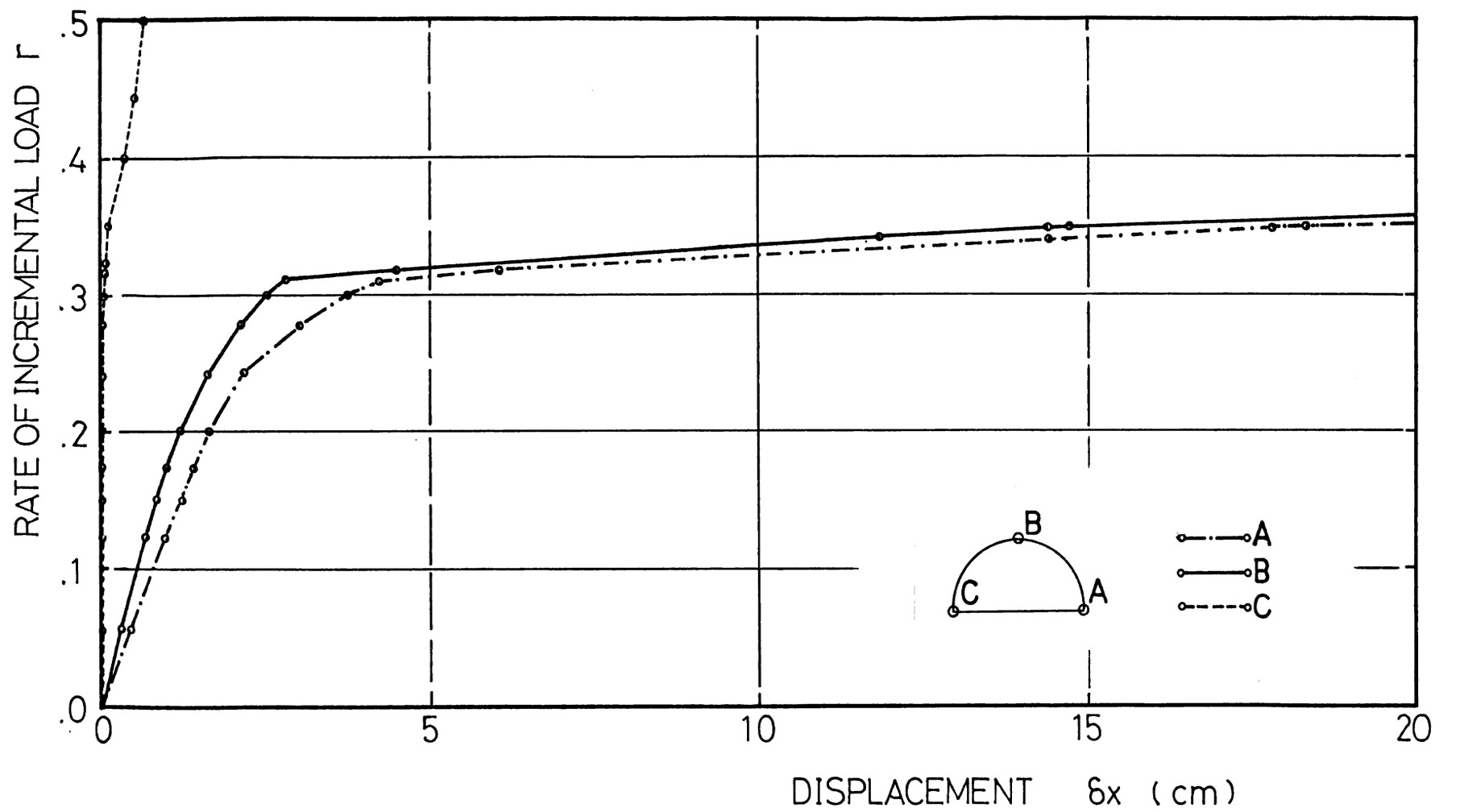
$\hspace{2em}$図6.38 素掘りトンネル周辺の荷重-変位曲線
これに対し、支保工を行った場合の結果が
図6.39に示されている。この結果は自重載荷率100%の状態で、
図(a)に示すすべり線は斜面内ばかりでなく、斜面前方にも広がっている。また、
図(b)に示した変位モードを眺めると斜面のはらみ出しがみられ、また、斜面上部の陥没も生じているため、斜面全体としては危険な状態にあるが、トンネルの形状は保たれている。
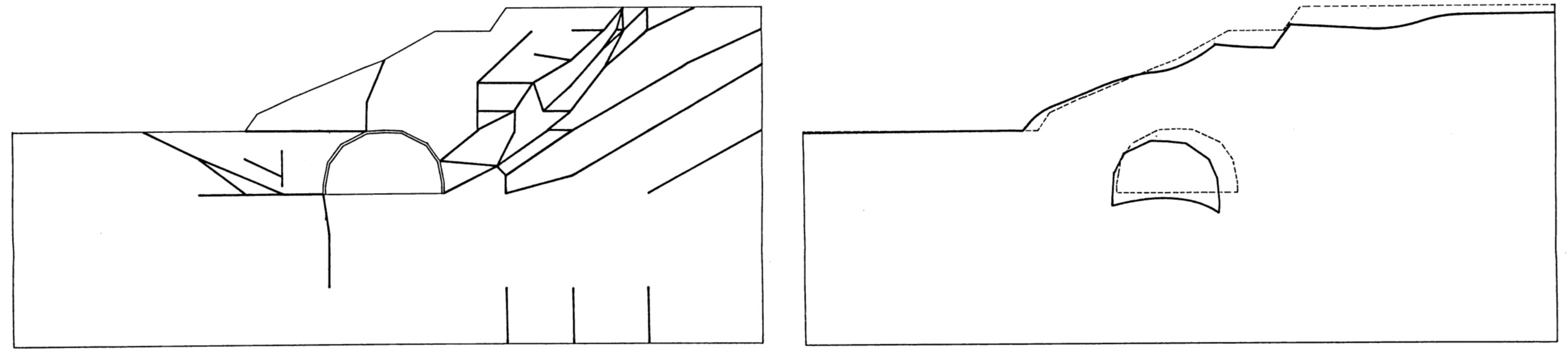
$\hspace{6em}$(a) すべり線
$\hspace{8em}$(b) 変位モード
$\hspace{10em}$図6.39 支保工を用いた場合の解析結果
以上、簡単な例により川井モデルによるトンネル問題の離散化極限解析結果を示したが、トンネル内を断層が横切ったり、ロックボルトが打設されているような複雑な問題にもこれまでの考え方を用いて容易に解析することが可能である。
3.5節で説明した接触を考慮した離散化極限解析法のアルゴリズムを検証する意味で、地中に埋め込まれたアンカーブロックの問題を取り上げてみよう。
図6.40(a)に示すよう、アンカーブロックが横方向の引張力 $P$ を受けるとブロック背面に引張力が生じ、その大きさによっては
図(b)に示すような分離が発生する。ここでは、このような問題に対して、山田の方法による荷重増分法のうち、すべりのみを考慮した解析法と
3.5節で示した接触を考慮した解析法の2つの解析法を適用し、得られる解の特性を比較してみる。
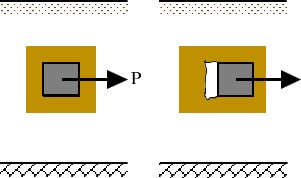
$\hspace{2em}$(a) 変形前
$\hspace{3em}$(b) 変形後
$\hspace{0em}$図6.40 アンカーブロックの挙動
図6.41には解析に用いたモデルと材料定数が示してある。ただし、この計算では接触効果を顕著に表すため、土の自重による影響は無視している。また、境界条件としては周辺スライドとした。
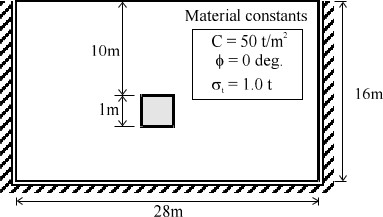
$\hspace{2em}$図6.41 アンカーブロックの解析モデル
図6.42には計算に用いた要素分割図が示してあり、節点数2324、要素数454、ばね数657、総自由度1362である。川井モデルの場合、要素自身を剛体と仮定し、要素境界辺 上に設けたばねの仕事を評価するため、要素形状は任意に設定することができる。そこで、剛体を仮定したアンカーブロックについては、図のように要素分割において1要素で表現している。
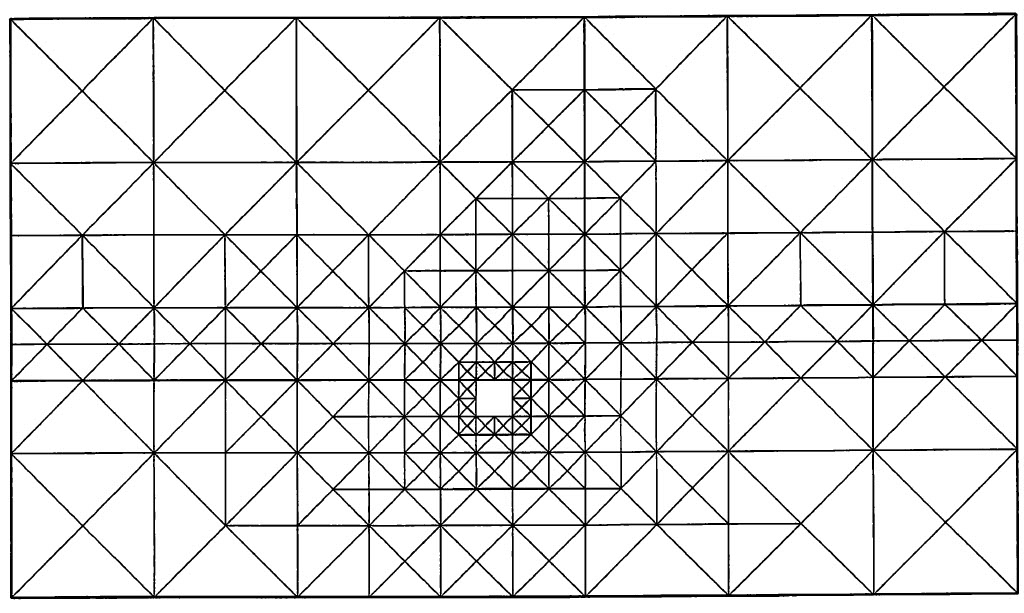
$\hspace{2em}$図6.42 アンカーブロックの要素分割
図6.43はすべりのみに着目して解析した結果で、荷重値 P=79.7tfにおけるすべり線が示されている。自重の影響が無ければ、アンカーブロック背面のすべりはあまり発生しないと思われるが、図では明らかにアンカーブロック前面と同じ程度のすべり線が背面にも発生している。
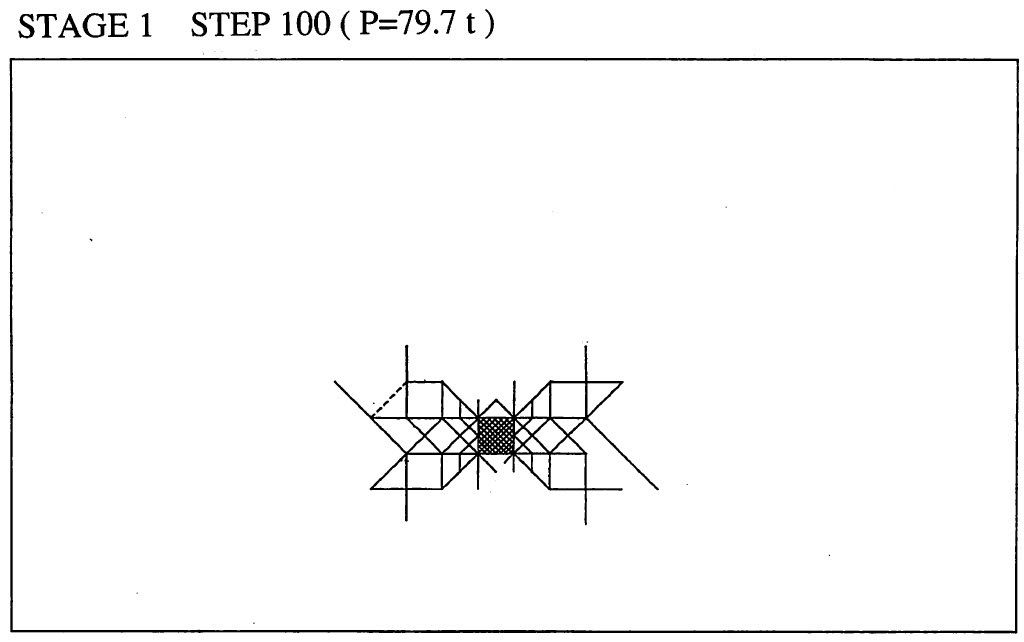
$\hspace{4em}$図6.43 すべり解析結果(すべり線)
このときの変位モードが
図6.44に示されている。すべり線発生状態ではよく理解できなかったが、ブロック背面の地盤がブロックに引きずられている様子が現れている。
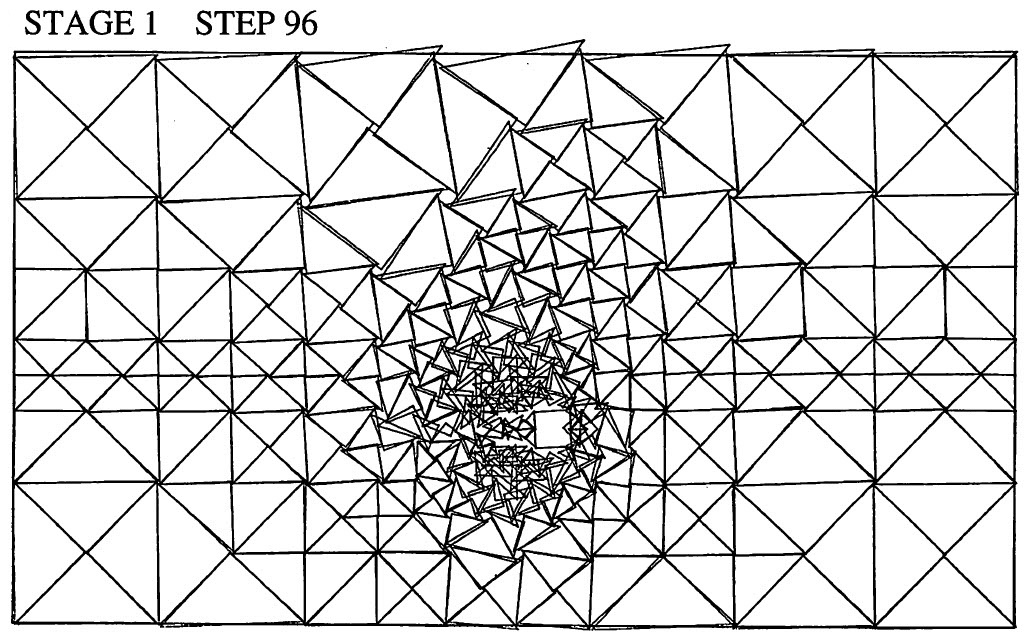
$\hspace{4em}$図6.44 すべり解析結果(変位モード)
一方、引張破壊や接触を考慮した解析において荷重増分量を
表6.2のように設定し、各荷重ステージにおいて山田の方法を適用しながら解析した。
表6.2 荷重増分量
| 荷重ステージ |
荷重値(t) |
| 1 |
10 |
| 2 |
10 |
| 3 |
5 |
| 4 |
5 |
| 5 |
5 |
| 合計 |
35 |
図6.45には荷重ステージ5、繰り返しステップ21におけるすべり線発生状況が示されている。図中、点線は引っ張りクラックを、また、実線はすべりを表している。明らかに、すべりのみの解析とは異なり、ブロック前方を中心として破壊が進行している。
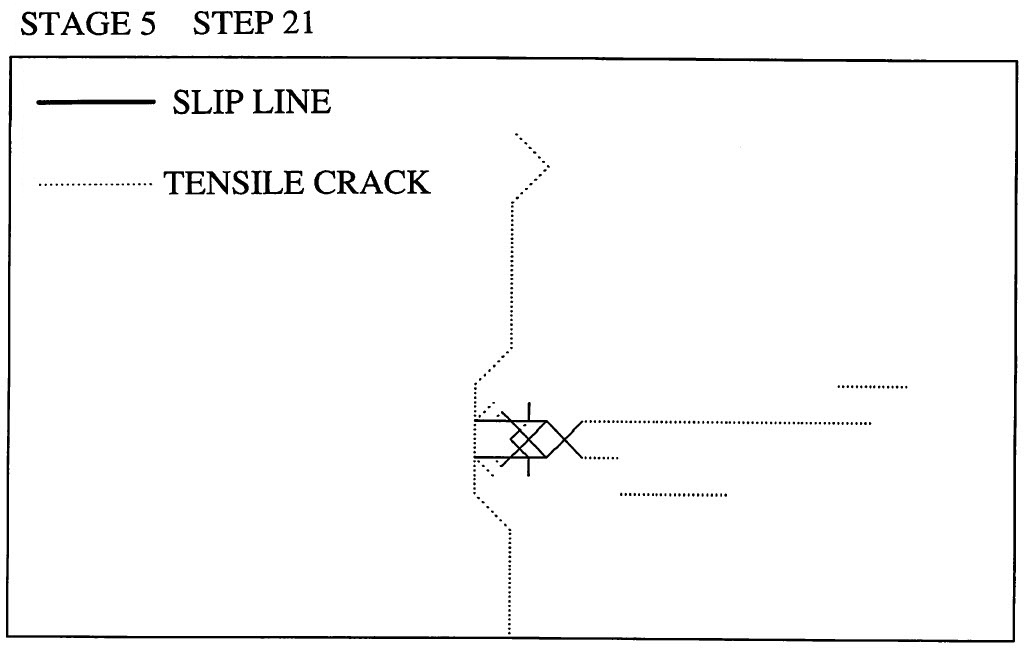
$\hspace{1em}$図6.45 接触を考慮したすべり解析結果(すべり線)
また、このときの変位モードおよび、変位ベクトルが
図6.46、
図6.47に示されている。ブロック背面においてブロックと地盤が分離し、ブロック前方の変位が卓越している様子がよく現れている。
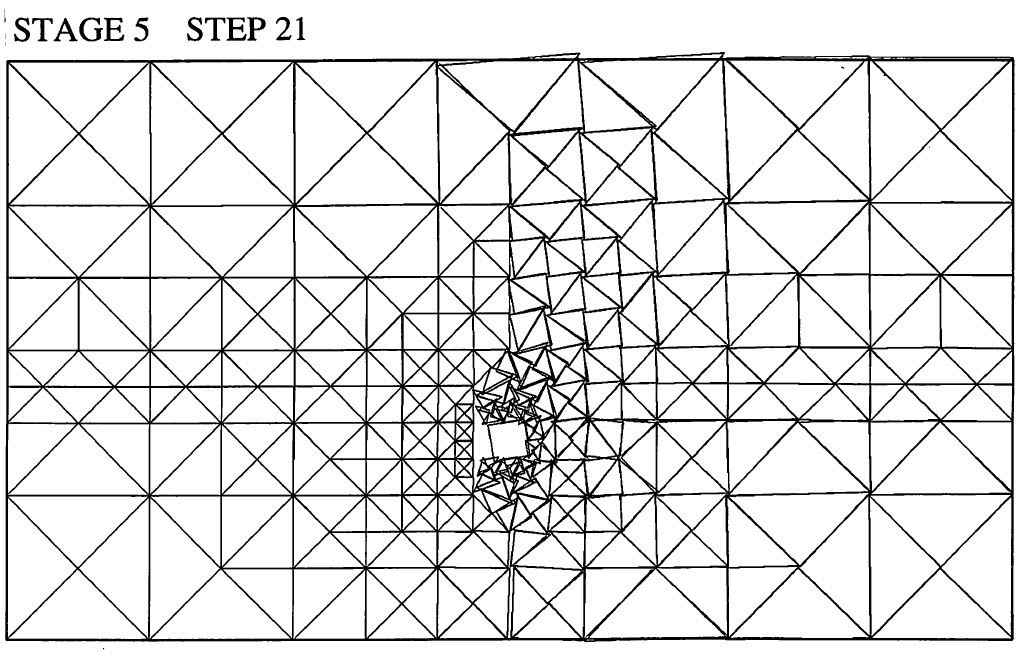
$\hspace{1em}$図6.46 接触を考慮したすべり解析結果(変位モード)
$\hspace{1em}$図6.47 接触を考慮したすべり解析結果(変位ベクトル)
以上の関係を荷重変位曲線により示した図が、
図6.48である。単純なすべりだけの荷重増分法ではブロック背面の土がブロックの運動を拘束する傾向にあるため、高い崩壊荷重を与える。これに対し、接触を考慮した解析法ではブロック背面における土砂の抵抗が無いため、すべりのみの解析に対し、極端に低い荷重で崩壊する傾向が現れている。
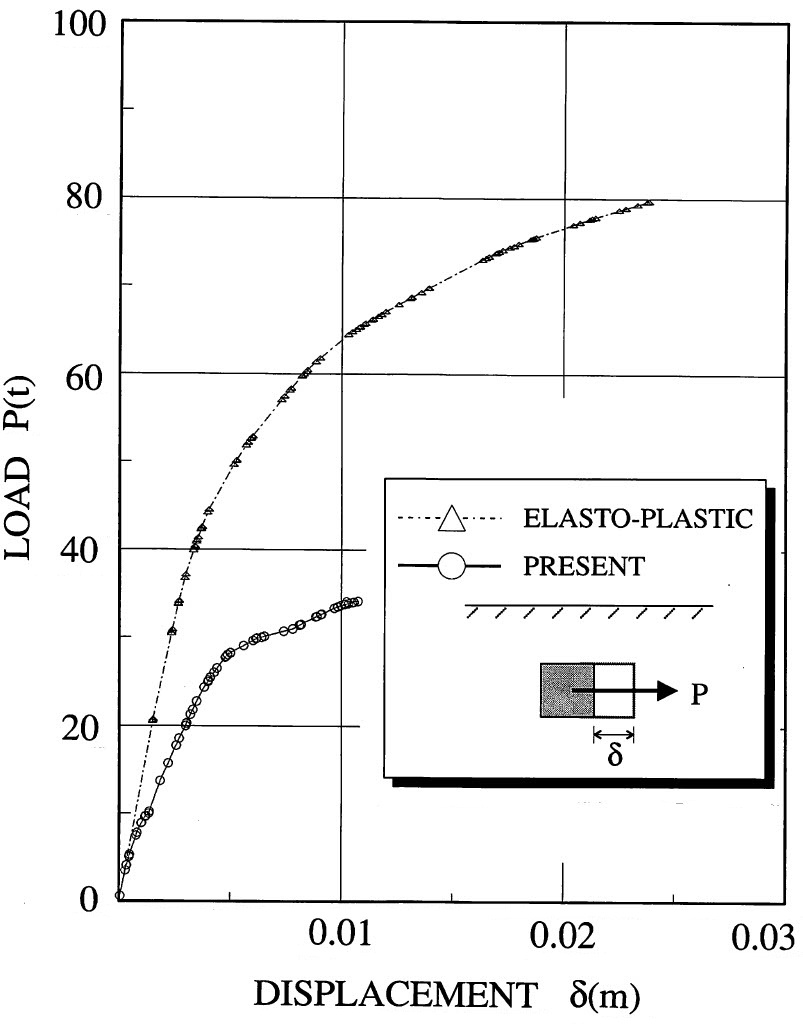
$\hspace{1em}$図6.48 アンカーブロックの荷重-変位曲線
本例題はアルゴリズムを検証する程度の簡単なモデルであるが、接触を考慮した場合とそうでない場合の得られ解の相違については理解できたと思う。このアルゴリズムは材料物性を検討するミクロ的な粒状体力学諸問題へも応用が可能であろう。