変位 $\boldsymbol{u} \left( \boldsymbol{x} \right) $ を小領域内の任意点 $\boldsymbol{x}_{_0} = (x_{_0},y_{_0}) \in \Omega^{(e)}$ についてテーラー展開し,1次の項までを表示すると以下のようになる.
\[
{\rm (2.1)}
\boldsymbol{u}^{(e)}
=
\boldsymbol{u} \left( \boldsymbol{x}_{_0} \right)
+
(x-x_{_0}) \boldsymbol{u}_x \left( \boldsymbol{x}_{_0} \right)
+
(y-y_{_0}) \boldsymbol{u}_y \left( \boldsymbol{x}_{_0} \right)
+
\cdots
\]
ここで,$\boldsymbol{u} \left( \boldsymbol{x}_{_0} \right)$ は小領域内の点 $\boldsymbol{x}_{_0}$における変位を示しており,また,
\[
( \bullet )_x = \frac{\partial}{\partial x}( \bullet )\;\;,\;\;
( \bullet )_y = \frac{\partial}{\partial y}( \bullet )
\]
一方,$x$方向変位を$u$,$y$方向変位を$v$とするとき,ひずみ-変位関係は以下のように与えられる.
\[ u_x = \varepsilon_x \;\;,\;\; v_y = \varepsilon_y
\]
\[
(v_x - u_y) = \theta \;,\; \frac{1}{2}(u_y+v_x) = \gamma_{xy}
\]
これらの関係を用いることによって
式(2.1)で示される線形の変位場は,マトリックス形式で次のように表すことができる.
\[
{\rm (2.2)}
\boldsymbol{u}^{(e)}
=
\boldsymbol{N}_d^{(e)} \boldsymbol{d}^{(e)}
+
\boldsymbol{N}_\varepsilon^{(e)} \boldsymbol{\varepsilon}^{(e)}
\]
ここで,上付きの $(e)$ は小領域 $\Omega^{(e)}$ に関するものであることを意味する.また,$\boldsymbol{d}^{(e)}$ は,小領域 $\Omega^{(e)}$ 内のある1点 $\boldsymbol{x}_{_0}$ における剛体変位 $(u_0,v_0)$ および剛体回転 $( \theta_0 )$ であり,$\boldsymbol{\varepsilon}^{(e)}$ は小領域内で一定なひずみで,それぞれ,以下のとおりである.
\[
\boldsymbol{u}^{(e)} = \lfloor u , v \rfloor^{t}
\hspace{2em}
\boldsymbol{d}^{(e)} = \lfloor u_0 , v_0 , \theta_0 \rfloor^{t}
\hspace{2em}
\boldsymbol{\varepsilon}^{(e)} =
\lfloor \varepsilon_{x_0} , \varepsilon_{y_0} , \gamma_{xy_0} \rfloor^{t}
\]
\[
\boldsymbol{N}_d^{(e)} =
\left[
\matrix{
1 & 0 & -Y^{(e)}\cr
0 & 1 & X^{(e)}
}
\right]
\hspace{2em}
\boldsymbol{N}_\varepsilon^{(e)} =
\left[
\matrix{
X^{(e)} & 0 & Y^{(e)}/2 \cr
0 & Y^{(e)} & X^{(e)}/2
}
\right]
\]
\[
\left.
\begin{array}{l}
X^{(e)} = x - x_{_0} \\
Y^{(e)} = y - y_{_0}
\end{array}
\right\}
\]
このように,本手法で用いる変位場は,領域内における任意点の剛体変位,剛体回転に加え,直接,ひずみを自由度として扱う.また,各領域内の任意点におけるパラメータを用いて変位場を表しているため,自由度を要素頂点に設定するような従来の変位型FEMの要素とは異なり,頂点において変位を共有しない.すなわち,本モデルにおける頂点は領域形状を認識するために用いるのであって,従来の変位型FEMのように頂点は形状関数に支配されない.したがって,領域形状は特に限定されず,任意の多角形,多面体,曲面体を小領域として用いることができる.
1.3節で述べたように,Lagrangeの未定乗数は,物理的には表面力を意味している.従来のハイブリッド型変分原理を用いる手法では,この未定乗数を要素境界辺上の点における値と補間関数を用いて表し,その値を未知数として重ね合わせを行い,全体係数行列を作成する.したがって,要素内変位場を独立に設定しても,この時点で要素形状は補間関数に依存し,何らかの拘束が生ずる.
一方,川井 は,表面力と相対変位の間にばねの概念を導入し,
\[
{\rm (2.3)}
\boldsymbol{\sigma}_{\lt ab \gt} = \boldsymbol{k} \cdot \boldsymbol{\delta}_{\lt ab \gt}
\]
とすることで,ばねによる表面力の仕事を用いて全体のエネルギーを評価する,
剛体-ばねモデル(RBSM)と呼ばれる方法を提案している.ここで,$\boldsymbol{\sigma}_{\lt ab \gt}=\lfloor \sigma_n , \tau \rfloor^{t}$ は要素境界面上の表面力を,$\boldsymbol{\delta}_{\lt ab \gt}=\lfloor \delta_n, \delta_s \rfloor^{t}$ は法線および接線方向の相対変位を,$\boldsymbol{k}$ はばね定数を表している.
一方,
ハイブリッド型ペナルティ法(HPM)では,Lagrangeの未定乗数 $\boldsymbol{\lambda}$ が表面力に対応するという物理的意味を考慮して,小領域 $\Omega^{(a)}$ と $\Omega^{(b)}$ における境界 $\Gamma_{\lt ab \gt}$ 上の表面力を以下のように表す.
\[
{\rm (2.4)}
\boldsymbol{\lambda}_{\lt ab \gt} = \boldsymbol{k} \cdot \boldsymbol{\delta}_{\lt ab \gt}
\]
2次元問題の場合,
式(2.4)を成分でで表すと以下のようになる.
\[
{\rm (2.5)}
\left\{
\begin{array}{c}
\lambda_n \\
\lambda_s
\end{array}
\right\}
=
\left[
\begin{array}{cc}
k_n & 0 \\
0 & k_s
\end{array}
\right]
\left\{
\begin{array}{c}
\delta_n \\
\delta_s
\end{array}
\right\}
\]
ここで,
図2.1に示すように,$\left( \delta_n, \delta_s \right)$ は要素境界辺に対する法線および接線方向の相対変位で,同様に,$\left( \lambda_n, \lambda_s \right)$ は,法線および接線方向に対するLagrangeの未定乗数,すなわち表面力である.
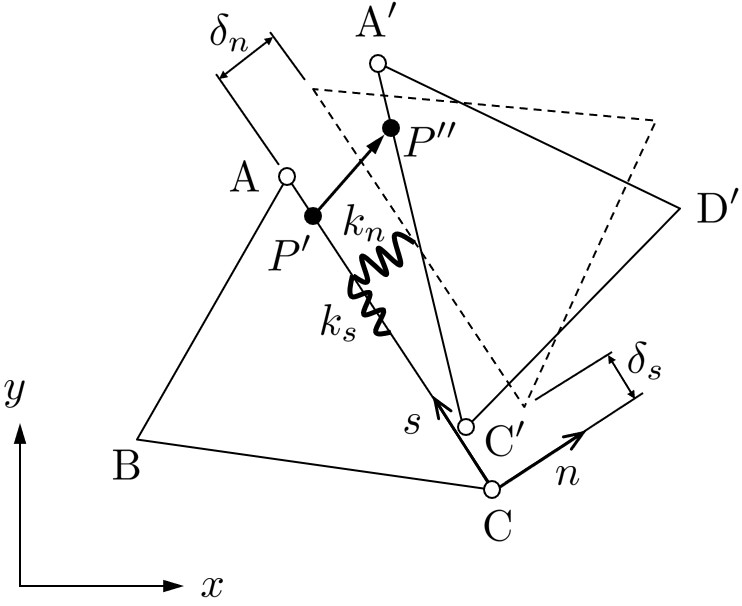
図2.1 全体座標系と局所座標系
RBSMでは,要素を剛体と仮定しているため,
式(2.3)で表されるばね $\left( k_n , k_s \right)$ に,
式(2.6)の変形特性を持たせる.
\[
{\rm (2.6)}
\mathbf{(平面ひずみ状態)}\hspace{2em}
\left.
\begin{array}{rl}
k_n &
\displaystyle \!\!\!\!\!
= \frac{(1-\nu)E}{(1-2 \nu)(1+\nu)}
\cdot \frac{1}{h_1+h_2} \\
k_s &
\displaystyle \!\!\!\!\!
= \frac{E}{1+\nu}
\cdot \frac{1}{h_1+h_2}
\end{array}
\right\}
\]
\[
{\rm (2.7)}
\mathbf{(平面応力状態)}\hspace{3em}
\left.
\begin{array}{rl}
k_n &
\displaystyle \!\!\!\!\!
= \frac{E}{(1- \nu^2)}
\cdot \frac{1}{h_1+h_2} \\
k_s &
\displaystyle \!\!\!\!\!
= \frac{E}{1+\nu}
\cdot \frac{1}{h_1+h_2} \\
\end{array}
\right\}
\]
ここで,$E$ は弾性係数,$\nu$ はポアソン比であり,$h_1, h_2$ は
図2.2に示される垂線の高さである.
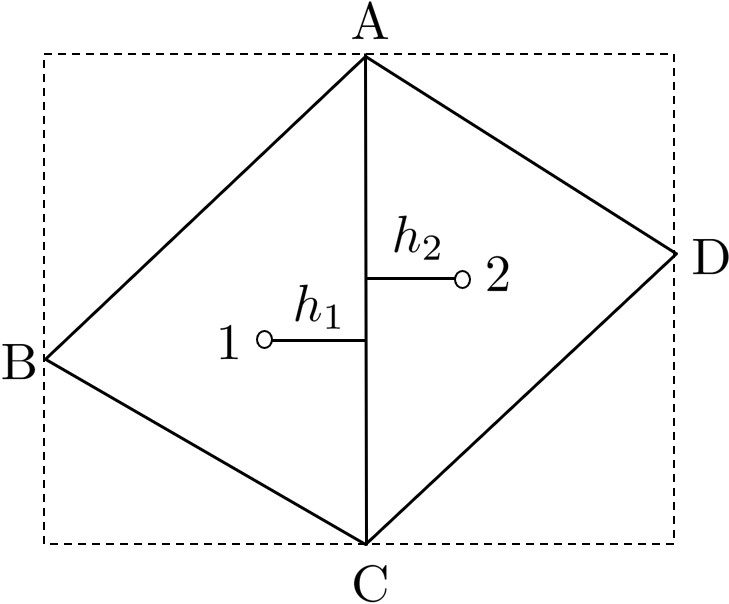
$\hspace{3em}$図2.2 垂線の高さ
一方,HPMでは小領域を弾性体としており,変形はこの小領域の変形によって表現される.したがって,
式(2.4)の $\boldsymbol{k}$ を,
式(2.6)あるいは
式(2.7)で示されるようなRBSMと同様な有限な値を有する「ばね」として表現することはできない.著者らは,この問題を解決するため,$\boldsymbol{k}$ としてペナルティ関数を用いる方法を提案した.これが,HPMの考え方で,
式(2.5)の係数 $\left( k_n , k_s \right)$ を
ペナルティ関数 $p$ により,以下のように表す.
\[
{\rm (2.8)}
k_n = k_s = p
\]
ところで,Shiらが提案したDDAも,HPMと同様にペナルティ関数を用いて,要素どうしを接続している.このDDAとHPMの大きな違いは,
図2.3に示すようなペナルティ関数の設置箇所である.DDAでは,動解析を行いDEMと同様な接触を考えるため,実用上,
図2.3(a)に示す点接触を採用している.一方,HPMでは,
図(b)に示すような面(辺)接触としている.
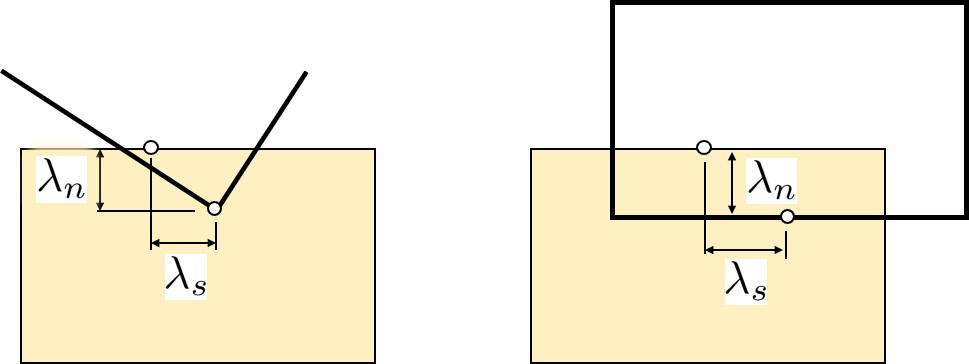
$\hspace{3em}$(a)点接触
$\hspace{7em}$(b)面接触
$\hspace{7em}$図2.3 垂線の高さ
この面接触の考え方は,RBSMと全く同じで,RBSM的な考え方をすれば,HPMでは極めて硬いばねを設定していることになる.こういった考えから,
式(2.8)で示したペナルティ関数に対して,RBSMの考え方に基づき,以下のような重みを付けたペナルティ関数を用いることも多い.
\[
{\rm (2.9)}
\mathbf{(平面ひずみ状態)}\hspace{2em}
\left.
\begin{array}{rl}
k_n &
\displaystyle \!\!\!\!\!
= \frac{(1-\nu)E'}{(1-2 \nu)(1+\nu)}
\cdot \frac{1}{h_1+h_2} \\
k_s &
\displaystyle \!\!\!\!\!
= \frac{E'}{1+\nu}
\cdot \frac{1}{h_1+h_2}
\end{array}
\right\}
\]
\[
{\rm (2.10)}
\mathbf{(平面応力状態)}\hspace{3em}
\left.
\begin{array}{rl}
k_n &
\displaystyle \!\!\!\!\!
= \frac{E'}{(1- \nu^2)}
\cdot \frac{1}{h_1+h_2} \\
k_s &
\displaystyle \!\!\!\!\!
= \frac{E'}{1+\nu}
\cdot \frac{1}{h_1+h_2} \\
\end{array}
\right\}
\]
ここで,$E'$ は以下のように,弾性係数にペナルティ関数をかけた値である.
\[
{\rm (2.11)}
E'= E \times p
\]
図2.4は小領域 $\Omega^{(e)}$ の境界 $\Gamma_{\lt s \gt}$ 上の座標系 $n-s$ と全体座標系 $x-y$ の関係を示した図である.
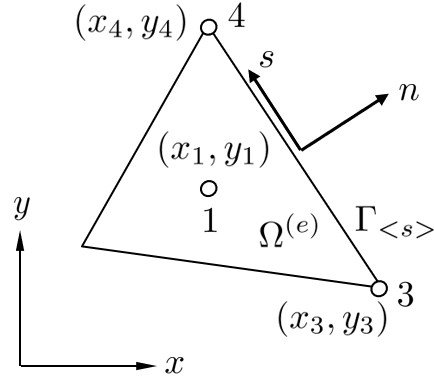
$\hspace{0em}$図2.4 局所座標系と全体座標系
小領域 $\Omega^{(e)}$ の境界面(辺)$\Gamma_{\lt s \gt}$ 上の変位を $\boldsymbol{u}^{(e)}_{\lt s \gt}$ とし,境界面(辺)に沿った局所座標系の変位を $\boldsymbol{u}^{(e)}_{n_{\lt s \gt}}$ とするとき,両者の間に以下の座標変換の関係が成立する.
\[
{\rm (2.12)}
\boldsymbol{u}^{(e)}_{n_{\lt s \gt}}
=
\boldsymbol{R}_{\lt s \gt}^{(e)}
\boldsymbol{u}^{(e)}_{\lt s \gt}
\]
ここで,$\boldsymbol{R}_{\lt s \gt}^{(e)}$ は小領域 $\Omega^{(e)}$ の境界辺における全体座標系から $\Gamma_{\lt s \gt}$ における局所座標系への座標変換行列である.いま,隣接する2つの小領域 $\Omega^{(a)}$ と $\Omega^{(b)}$ の共通の境界辺を $\Gamma_{\lt ab \gt}$ とするとき,以下の関係がある.
\[
{\rm (2.13)}
\boldsymbol{R}_{\lt ab \gt}
=
-\boldsymbol{R}_{\lt ab \gt}^{(a)}
=
\boldsymbol{R}_{\lt ab \gt}^{(b)}
\]
以下に,具体的に2次元問題における座標変換行列 $\boldsymbol{R}_{\lt s \gt}^{(e)}$ を示す.
\[
{\rm (2.14)}
\boldsymbol{R}_{\lt s \gt}^{(e)}
=
\left[
\begin{array}{cc}
l_1 & m_1 \\
l_3 & m_3
\end{array}
\right]
\]
ここで,$l_1, m_1, l_3, m_3$ は方向余弦で,図中の座標値を用いると以下のようになる.
\[
l_1 = \frac{x_{43}}{L} ,
m_1 = \frac{y_{43}}{L} ,
l_3 = m_1 , m_3 = -l_1
\]
\[
L = \sqrt{x_{43}^2 + y_{43}^2} ,
\left( x_{ij} = x_i - x_j \right)
\]
以上の関係を用いると小領域 $\Omega^{(a)}$ と $\Omega^{(b)}$ の共通の境界辺を $\Gamma_{\lt ab \gt}$ 上の相対変位 $\boldsymbol{\delta}_{\lt ab \gt}$ は次のように表される.
\[
{\rm (2.15)}
\boldsymbol{\delta}_{\lt ab \gt}
=
\boldsymbol{R}_{\lt ab \gt}^{(a)} \boldsymbol{u}_{\lt ab \gt}^{(a)}
+
\boldsymbol{R}_{\lt ab \gt}^{(b)} \boldsymbol{u}_{\lt ab \gt}^{(b)}
=
\sum_{e=1}^{2}
\boldsymbol{R}^{(e)}_{\lt ab \gt} \boldsymbol{u}_{\lt ab \gt}^{(e)}
\]
一方,
式(1.17)で表された付帯条件は,小領域 $\Omega^{(e)}$ の境界辺 $\Gamma_{\lt s \gt}$ 上の変位を全体座標系で表したものであった.これを,境界面辺 $\Gamma_{\lt s \gt}$ に沿った局所座標系で表すことも可能である.いま,
式(2.12)を用い,隣接する2つの小領域 $\Omega^{(a)}$ と $\Omega^{(b)}$ と,共通の境界面 $\Gamma_{\lt ab \gt}$ において付帯条件の式に座標変換行列をかけると,
式(2.13)の関係を用いて次のようになる.
\[
{\rm (2.16)}
\boldsymbol{R}_{\lt ab \gt}^{(a)} \boldsymbol{u}_{\lt ab \gt}^{(a)}
+
\boldsymbol{R}_{\lt ab \gt}^{(b)} \boldsymbol{u}_{\lt ab \gt}^{(b)}
= 0
\]
局所座標系で表されたこの付帯条件をLagrangeの未定乗数 $\boldsymbol{\lambda}$ を用いて以下のように表し,仮想仕事式に導入する.
\[
{\rm (2.17)}
H_{ab}
\stackrel{\rm def.}{=}
\delta \int_{\Gamma_{\lt ab \gt}} \boldsymbol{\lambda} \! \cdot \!
\left(
\boldsymbol{R}_{\lt ab \gt}^{(a)} \boldsymbol{u}_{\lt ab \gt}^{(a)}
+
\boldsymbol{R}_{\lt ab \gt}^{(b)} \boldsymbol{u}_{\lt ab \gt}^{(b)}
\right)\; dS
\]
ここで,
式(2.15)を用いれば,上式は以下のように表すことができる.
\[
{\rm (2.18)}
H_{ab}
=
- \delta
\int_{\Gamma_{\lt ab \gt}} \boldsymbol{\lambda} \! \cdot \!
\boldsymbol{\delta}_{\lt ab \gt}
\; dS
\]
一方,Lagrangeの未定乗数 $\boldsymbol{\lambda}$ は,
式(2.4)のように仮定しているため,
式(2.18)は次のように表すことができる.
\[
{\rm (2.19)}
H_{ab}
=
- \delta
\int_{\Gamma_{\lt ab \gt}}
\boldsymbol{\delta}_{\lt ab \gt}^t
\! \cdot \!
\boldsymbol{k}
\! \cdot \!
\boldsymbol{\delta}_{\lt ab \gt}
\; dS
\]
したがって,ハイブリッド型の仮想仕事
式(1.19)は次のように書くことができる.
\[
{\rm (2.20)}\\
\sum_{e=1}^{M}
\left(
\int_{\Omega^{(e)}} \boldsymbol{\sigma} \! : \! {\rm grad} \delta \boldsymbol{u} \: dV
- \int_{\Omega^{(e)}} \boldsymbol{f} \! \cdot \! \delta \boldsymbol{u} dV
- \int_{\Gamma^{(e)}} \boldsymbol{t}\! \cdot \! \delta \boldsymbol{u} \: dS
\right)
-
\sum_{s=1}^{N}
\left(
\delta \int_{\Gamma_{\lt s \gt}}
\boldsymbol{\delta}^t \boldsymbol{k} \boldsymbol{\delta}
\; dS
\right)
= 0
\]
ハイブリッド型仮想仕事
式(2.20)に対して小領域毎に独立な線形の変位場の
式(2.2)を代入する.さらに,仮想変位についても変位と同様に,以下のように仮定して
式(2.20)へ代入する.
\[
{\rm (2.21)}
\delta \boldsymbol{u}^{(e)}
=
\boldsymbol{N}_d^{(e)} \delta \boldsymbol{d}^{(e)}
+
\boldsymbol{N}_\varepsilon^{(e)} \delta \boldsymbol{\varepsilon}^{(e)}
\]
いま,簡単のため,
式(2.2)および
式(2.21)を以下のようにまとめる.
\[
{\rm (2.22)}
\boldsymbol{u}^{(e)} = \boldsymbol{N}^{(e)} \boldsymbol{U}^{(e)}
\]
\[
{\rm (2.23)}
\delta \boldsymbol{u}^{(e)} = \boldsymbol{N}^{(e)} \delta \boldsymbol{U}^{(e)}
\]
ここで,それぞれの係数は以下のとおりである.
\[\hspace{5em}
\boldsymbol{U}^{(e)} =
\lfloor
\boldsymbol{d}^{(e)}
,
\boldsymbol{\varepsilon}^{(e)}
\rfloor^t
\]
\[\hspace{5em}
\delta \boldsymbol{U}^{(e)} =
\lfloor
\delta \boldsymbol{d}^{(e)}
,
\delta \boldsymbol{\varepsilon}^{(e)}
\rfloor^t
\]
\[\hspace{5em}
\boldsymbol{N}^{(e)}
=
\lfloor
\boldsymbol{N}^{(e)}_d
,
\boldsymbol{N}^{(e)}_{\varepsilon}
\rfloor
\]
このとき,
式(2.20)の第1項は以下のように展開できる.
\[
{\rm (2.24)}
\int_{\Omega^{(e)}} \boldsymbol{\sigma} \! : \! {\rm grad} \delta \boldsymbol{u} \: dV
=
\left( \delta \boldsymbol{U}^{(e)} \right)^t
\int_{\Omega^{(e)}} {}^t \boldsymbol{B}^{(e)} \boldsymbol{D}^{(e)}
\boldsymbol{B}^{(e)} \; dV \;
\boldsymbol{U}^{(e)}
\]
\[\hspace{13em}
=
\left( \delta \boldsymbol{U}^{(e)} \right)^t
\boldsymbol{k}^{(e)}
\boldsymbol{U}^{(e)}
\]
ここで,
\[
{\rm (2.25)}
\boldsymbol{k}^{(e)}
=
\int_{\Omega^{(e)}}
{}^t \boldsymbol{B}^{(e)} \boldsymbol{D}^{(e)} \boldsymbol{B}^{(e)}
\; dV
\]
であり,$\boldsymbol{D}^{(e)}$ は小領域 $\Omega^{(e)}$ の構成行列で,弾性の場合,
式(1.8)(1.9)で表される.また,$\boldsymbol{B}^{(e)}$ はひずみ-変位行列で,2次元問題の場合,以下のように表される.
\[
{\rm (2.26)}
\boldsymbol{B}^{(e)}
=
\left[
\matrix{
0 & 0 & 0 & 1 & 0 & 0 \cr
0 & 0 & 0 & 0 & 1 & 0 \cr
0 & 0 & 0 & 0 & 0 & 1
}
\right]
\]
いま,$\boldsymbol{\cal A}^{(e)}$ を,全部分領域 $\Omega = \bigcup_{e=1}^{M} \Omega^{(e)}$ における自由度 $\boldsymbol{U}$ と着目部分領域 $\Omega^{(e)}$ における自由度 $\boldsymbol{U}^{(e)}$ を関係付ける行列とする.このとき,変位と仮想変位は,以下のように表すことができる.
\[
{\rm (2.27)}
\boldsymbol{U}^{(e)} =
\boldsymbol{\cal A}^{(e)} \boldsymbol{U}
\]
\[
{\rm (2.28)}
\delta \boldsymbol{U}^{(e)} =
\boldsymbol{\cal A}^{(e)} \delta \boldsymbol{U}
\]
この関係を
式(2.24)に適用すると以下のようになる.
\[
{\rm (2.29)}
\int_{\Omega^{(e)}}
\boldsymbol{\sigma}
\! : \!
{\rm grad} \delta \boldsymbol{u}
\: dV
=
\delta \boldsymbol{U}^t
\boldsymbol{K}^{(e)}
\boldsymbol{U}
\hspace{3em}
\left(
\boldsymbol{K}^{(e)} =
{}^t \boldsymbol{\cal A}^{(e)}
\boldsymbol{k}^{(e)}
\boldsymbol{\cal A}^{(e)}
\right)
\]
一方,
式(2.20)の第2項は物体力による荷重項で,以下のように展開できる.
\[
{\rm (2.30)}
\int_{\Omega^{(e)}} \boldsymbol{f} \! \cdot \! \delta \boldsymbol{u} dV
=
\left( \delta \boldsymbol{U}^{(e)} \right)^t
\left(
\int_{\Omega^{(e)}} {}^t \boldsymbol{N}^{(e)} \boldsymbol{f} \; dV
\right)
=
\left( \delta \boldsymbol{U}^{(e)} \right)^t
\boldsymbol{w}_f^{(e)}
\]
\[\hspace{6em}ただし
\left(
\boldsymbol{w}_f^{(e)}
=
\int_{\Omega^{(e)}}
{}^t \boldsymbol{N}^{(e)}
\boldsymbol{f} \; dV
\right)
\]
また,第3項は表面力による荷重項で,上式と同様に以下のように展開できる.
\[
{\rm (2.31)}
\int_{\Gamma^{(e)}} \boldsymbol{t} \! \cdot \! \delta \boldsymbol{u} dS
=
\left( \delta \boldsymbol{U}^{(e)} \right)^t
\left(
\int_{\Gamma^{(e)}}
{}^t \boldsymbol{N}^{(e)}
\boldsymbol{t} \; dS
\right)
=
\left( \delta \boldsymbol{U}^{(e)} \right)^t
\boldsymbol{p}_t^{(e)}
\]
\[\hspace{6em}ただし
\left(
\boldsymbol{p}_t^{(e)}
=
\int_{\Gamma^{(e)}}
{}^t \boldsymbol{N}^{(e)}
\boldsymbol{t}
\; dS
\right)
\]
これら2つの荷重項に対して
式(2.28)を適用し一つにまとめると以下のように整理できる.
\[
{\rm (2.32)}
\int_{\Omega^{(e)}}
\boldsymbol{f} \! \cdot \! \delta \boldsymbol{u}
dV
+
\int_{\Gamma^{(e)}}
\boldsymbol{t} \! \cdot \! \delta \boldsymbol{u}
dS
=
\delta \boldsymbol{U}^t \boldsymbol{W}_f^{(e)}
+
\delta \boldsymbol{U}^t \boldsymbol{P}_t^{(e)}
=
\delta \boldsymbol{U}^t \boldsymbol{P}^{(e)}
\]
ここで,
\[\hspace{5em}
\boldsymbol{W}_f^{(e)} = {}^t \boldsymbol{\cal A}^{(e)} \boldsymbol{w}_f^{(e)}
\]
\[\hspace{5em}
\boldsymbol{P}_t^{(e)} = {}^t \boldsymbol{\cal A}^{(e)} \boldsymbol{p}_t^{(e)}
\]
\[\hspace{5em}
\boldsymbol{P}^{(e)} = \boldsymbol{W}_f^{(e)} + \boldsymbol{P}_t^{(e)}
\]
以上の関係を整理すると,小領域 $\Omega^{(e)}$ における仮想仕事式 $\delta W^{(e)}$ に対する離散化式が以下のように求まる.
\[
{\rm (2.33)}
\delta W^{(e)}
=
\delta \boldsymbol{U}^t \boldsymbol{K}^{(e)} \boldsymbol{U}
-
\delta \boldsymbol{U}^t \boldsymbol{P}^{(e)}
\]
さて,
式(2.20)における付帯条件の項を離散化するにあたり,
式(2.15)で表される相対変位を以下のように整理する.
\[
{\rm (2.34)}
\boldsymbol{\delta}_{\lt ab \gt}
=
\boldsymbol{B}_{\lt ab \gt}
\boldsymbol{U}_{\lt ab \gt}
\]
ここで,
\[\hspace{5em}
\boldsymbol{B}_{\lt ab \gt}
=
\lfloor
\boldsymbol{R}_{\lt ab \gt}^{(a)} \boldsymbol{N}^{(a)}
,
\boldsymbol{R}_{\lt ab \gt}^{(b)} \boldsymbol{N}^{(b)}
\rfloor
\]
\[\hspace{5em}
\boldsymbol{U}_{\lt ab \gt}
=
\lfloor
\boldsymbol{U}^{(a)} , \boldsymbol{U}^{(b)}
\rfloor^t
\]
この関係を用いると,付帯条件の項は以下のように整理できる.
\[
{\rm (2.35)}
H_{\lt ab \gt}
=
-\delta \int_{\Gamma_{\lt ab \gt}} \boldsymbol{\delta}^t_{\lt ab \gt} \cdot
\boldsymbol{k} \cdot \boldsymbol{\delta}_{\lt ab \gt} \; dS
\]
\[\hspace{8em}
=
-\delta \boldsymbol{U}_{\lt ab \gt}^t
\int_{\Gamma_{\lt ab \gt}} \boldsymbol{B}_{\lt ab \gt}^t
\boldsymbol{k}
\boldsymbol{B}_{\lt ab \gt}\; dS \;
\boldsymbol{U}_{\lt ab \gt}
\]
\[\hspace{8em}
=
-\delta \boldsymbol{U}_{\lt ab \gt}^t
\boldsymbol{k}_{\lt ab \gt}
\boldsymbol{U}_{\lt ab \gt}
\]
\[\hspace{8em}
\left(
\boldsymbol{k}_{\lt ab \gt}
=
\int_{\Gamma_{\lt ab \gt}} \boldsymbol{B}_{\lt ab \gt}^t
\boldsymbol{k}
\boldsymbol{B}_{\lt ab \gt}\; dS
\right)
\]
いま,$\boldsymbol{\cal M}_{\lt s \gt}$ を全自由度 $\boldsymbol{U}$ と着目境界面 $\Gamma_{\lt s \gt}$における自由度 $\boldsymbol{U}_{\lt s \gt}$ とを関係付ける行列とする.このとき,変位と仮想変位は,以下のように表すことができる.
\[
{\rm (2.36)}
\boldsymbol{U}_{\lt s \gt} =
\boldsymbol{\cal M}_{\lt s \gt} \boldsymbol{U}
\]
\[
{\rm (2.37)}
\delta \boldsymbol{U}_{\lt s \gt} =
\boldsymbol{\cal M}_{\lt s \gt} \delta \boldsymbol{U}
\]
この関係を用いると,
式(2.35)は次のように展開できる.
\[
{\rm (2.38)}
H_{\lt s \gt}
=
- \delta \boldsymbol{U}^t \boldsymbol{K}_{\lt s \gt} \boldsymbol{U}
\]
以上より,ハイブリッド型仮想仕事
式(2.20)は,
式(2.33),式(2.38)より次のようになる.
\[
{\rm (2.39)}
\sum_{e=1}^M \delta W^{(e)}
+
\sum_{s=1}^N H_{\lt s \gt}
= 0
\]
すなわち,
\[
{\rm (2.40)}
\delta \boldsymbol{U}^t
\left(
\sum_{e=1}^{M} \boldsymbol{K}^{(e)}
+
\sum_{s=1}^{N} \boldsymbol{K}_{\lt s \gt}
\right)
\boldsymbol{U}
-
\delta \boldsymbol{U}^t
\left(
\sum_{e=1}^{M} \boldsymbol{W}_f^{(e)}
+
\sum_{e=1}^{M} \boldsymbol{P}^{(e)}
\right)
= 0
\]
ここで,仮想変位 $\delta \boldsymbol{U}$ は任意であるため,最終的に以下の離散化方程式が得られる.
\[
{\rm (2.41)}
\boldsymbol{KU} = \boldsymbol{P}
\]
ただし,$\boldsymbol{K}$ および $\boldsymbol{P}$ は以下のとおりである.
\[
{\rm (2.42)}
\boldsymbol{K} =
\sum_{e=1}^{M} \boldsymbol{K}^{(e)}+
\sum_{s=1}^{N} \boldsymbol{K}_{\lt s \gt}
\]
\[
{\rm (2.43)}
\boldsymbol{P} =
\sum_{e=1}^{M} \boldsymbol{P}^{(e)}
\]
このように,本モデルの離散化方程式は,
式(2.41)に示す連立1次方程式に帰着し,左辺の係数行列 $\boldsymbol{K}$ は,各要素の剛性と要素境界辺に関する付帯条件の関係を組み合わせることによって得られる.
なお,係数行列 $\boldsymbol{K}_{\lt s \gt}$ において,要素境界面に関する積分が含まれるが,通常は数値積分により解析する.なお,Voronoi多角形など,多角形の複雑な形状の場合には数値積分の適用が難しくなる.このような場合,多角形を三角形の集まりに分割し,それぞれの三角形に対して数値積分を適用するという方法が提案されており,この方法を用いても精度に与える影響は少ないとされている.
FEMでは通常,節点に変位の自由度を設定し,変位に関する拘束があればこの節点の変位を拘束する.また,RBSMでは変位を拘束したい箇所に境界用要素を設け,その自由度を拘束することが通常行われている.どちらの方法も直接自由度を拘束しており,剛性方程式に対する拘束条件の処理方法は同じ扱いとなる.
一方,HPMは,小領域の内部に自由度が設定されるため,FEMのように直接自由度を拘束することは適切ではない.また,RBSMのような境界要素を用いることもできるが,境界用の要素のひずみ自由度を消去する必要が生じる.そこで,HPMでは,
図2.5に示すよう,拘束したい位置の変位を,ペナルティ関数を用いて拘束する,間接的に変位を拘束する方法が用いられている.
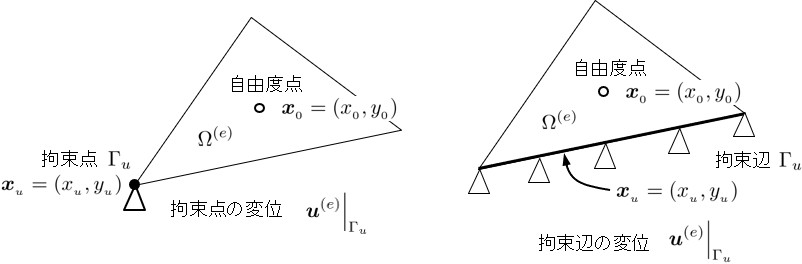
$\hspace{7em}$(a)節点の拘束
$\hspace{8em}$(b)辺の拘束
$\hspace{12em}$図2.5 HPMの拘束条件
いま,変位を拘束する節点や辺の境界を $\Gamma_u$,拘束変位を $\hat{\boldsymbol{u}}$ し,境界 $\Gamma_u$ に関係する小領域 $\Omega^{(e)}$ の $\Gamma_u$ 上の変位を $\left. \boldsymbol{u}^{(e)} \right|_{\Gamma_u}$ とするとき,境界条件は,
\[
{\rm (2.44)}
\left. \boldsymbol{u}^{(e)} \right|_{\Gamma_u}
=
\hat{ \boldsymbol{u} } \;\; {\rm (given)}
\]
と表される.この付帯条件をLagrangeに未定乗数 $\boldsymbol{\lambda}$ を用いて
\[
{\rm (2.45)}
H_u
=
\delta
\int_{\Gamma_u}
\boldsymbol{\lambda}
\left(
\hat{ \boldsymbol{u} }
-
\left.
\boldsymbol{u}^{(e)}
\right|_{\Gamma_u}
\right)
dS
\]
と表し,ハイブリッド型の仮想仕事式に考慮することで,間接的に拘束条件を導入する.
図2.5のように節点や辺を拘束する場合,
式(2.2)で表される変位場の関係を用いて以下のように求められる.
\[
{\rm (2.46)}
\left.
\boldsymbol{u}^{(e)}
\right|_{\Gamma_u}
=
\left.
\boldsymbol{N}_d^{(e)}
\right|_{\Gamma_u}
\boldsymbol{d}^{(e)}
+
\left.
\boldsymbol{N}_\varepsilon^{(e)}
\right|_{\Gamma_u}
\boldsymbol{\varepsilon}^{(e)}
\]
ここで,
\[\hspace{5em}
\left.
\boldsymbol{N}_d^{(e)}
\right|_{\Gamma_u}
=
\left[
\matrix{
1 & 0 & -(y_u-y_{_0}) \cr
0 & 1 & (x_u-x_{_0})
}
\right]
\]
\[\hspace{5em}
\left.
\boldsymbol{N}_\varepsilon^{(e)}
\right|_{\Gamma_u}
=
\left[
\matrix{
(x_u-x_{_0}) & 0 & (y_u-y_{_0})/2 \cr
0 & (y_u-y_{_0}) & (x_u-x_{_0})/2
}
\right]
\]
これを簡単に次のようにまとめる.
\[
{\rm (2.47)}
\left.
\boldsymbol{u}^{(e)}
\right|_{\Gamma_u}
=
\left.
\boldsymbol{N}^{(e)}
\right|_{\Gamma_u}
\boldsymbol{U}^{(e)}
\]
ここで,
\[\hspace{5em}
\left.
\boldsymbol{N}^{(e)}
\right|_{\Gamma_u}
=
\lfloor
\left.
\boldsymbol{N}^{(e)}_d
\right|_{\Gamma_u}
,
\left.
\boldsymbol{N}^{(e)}_{\varepsilon}
\right|_{\Gamma_u}
\rfloor
\]
このように,HPMでは,小領域 $\Omega^{(e)}$ の変位場を用いて,拘束境界点や辺 $\Gamma_u$ の変位 $\left. \boldsymbol{u}^{(e)} \right|_{\Gamma_u} $ を求めているため,プログラムにおける入力データでは,小領域番号と拘束位置を指定する必要がある.なお,
図(a)のように節点を拘束する場合は,
式(2.45)における積分は不要になる.
次に,
式(2.45)のLagrangeの未定乗数 $\boldsymbol{\lambda}$ について考えてみよう.この $\boldsymbol{\lambda}$ も,拘束点もしくは辺と小領域内の拘束点あるいは辺上の変位との間の表面力となる.そこで,
式(2.4) と同様,この $\boldsymbol{\lambda}$ を以下のように仮定する.
\[
{\rm (2.48)}
\left.
\boldsymbol{\lambda}
\right|_{\Gamma_u}
=
\boldsymbol{k}
\cdot
\left.
\boldsymbol{\delta}
\right|_{\Gamma_u}
\]
ただし,$\boldsymbol{k}$ はペナルティ関数である.また,$\left. \boldsymbol{\delta} \right|_{\Gamma_u}$ は以下の関係にある.
\[
{\rm (2.49)}
\left.
\boldsymbol{\delta}
\right|_{\Gamma_u}
=
\hat{ \boldsymbol{u} }
-
\left.
\boldsymbol{u}^{(e)}
\right|_{\Gamma_u}
\]
したがって,
式(2.45)は,以下のように整理できる.
\[
{\rm (2.50)}
H_u =
\delta \int_{\Gamma_u}
\left.
{}^t \boldsymbol{\delta} \right|_{\Gamma_u} \boldsymbol{k}
\left.
\boldsymbol{\delta} \right|_{\Gamma_u}
dS
\]
\[\hspace{6.5em}
=
\left( \delta \boldsymbol{U}^{(e)} \right)^t
\int_{\Gamma_u}
\left.
{}^t \boldsymbol{N}^{(e)}
\right|_{\Gamma_u}
\boldsymbol{k}
\left.
\boldsymbol{N}^{(e)}
\right|_{\Gamma_u}
dS
\boldsymbol{U}^{(e)}
-
\left(
\delta \boldsymbol{U}^{(e)}
\right)^t
\int_{\Gamma_u}
\left.
{}^t \boldsymbol{N}^{(e)}
\right|_{\Gamma_u}
\boldsymbol{k}
dS
\hat{\boldsymbol{u}}
\]
\[\hspace{6.5em}
=
\left( \delta \boldsymbol{U}^{(e)} \right)^t
\boldsymbol{k}_u^{(e)}
\boldsymbol{U}^{(e)}
-
\left( \delta \boldsymbol{U}^{(e)} \right)^t
\boldsymbol{p}_u^{(e)}
\hat{\boldsymbol{u}}
\]
ここで,
\[\hspace{5em}
\boldsymbol{k}_u^{(e)}
=
\int_{\Gamma_u}
\left. {}^t \boldsymbol{N}^{(e)} \right|_{\Gamma_u}
\boldsymbol{k}
\left. \boldsymbol{N}^{(e)} \right|_{\Gamma_u}
dS
\]
\[\hspace{5em}
\boldsymbol{p}_u^{(e)}
=
\int_{\Gamma_u}
\left.
{}^t \boldsymbol{N}^{(e)}
\right|_{\Gamma_u}
\boldsymbol{k}
dS
\]
したがって,
式(2.27),(2.28)の関係を用いると以下のように表すことができる.
\[
{\rm (2.51)}
H_u
=
\left( \delta \boldsymbol{U} \right)^t
\boldsymbol{K}_u^{(e)}
\boldsymbol{U}
-
\left( \delta \boldsymbol{U} \right)^t
\boldsymbol{P}_u^{(e)}
\hat{\boldsymbol{u}}
\]
ここで,
\[\hspace{5em}
\boldsymbol{K}_u^{(e)}
=
{}^t
\boldsymbol{\cal A}^{(e)}
\boldsymbol{k}_u^{(e)}
\boldsymbol{\cal A}^{(e)}
\]
\[\hspace{5em}
\boldsymbol{P}_u^{(e)}
=
{}^t
\boldsymbol{\cal A}^{(e)}
\boldsymbol{p}_u^{(e)}
\]
具体的には,
式(2.51)の左辺第1項は剛性行列に加算し,第2項は,拘束変位量が0でなければ,右辺の荷重項に加算すればよい.また,
式(2.51)において,拘束自由度が1方向の場合は,
式(2.47)を,該当自由度のみで表し,後の展開を行えばよい.




