剛体-ばねモデル(RBSM)ではFEMのように要素内応力ではなく,要素境界辺上における法線方向及びせん断方向に関する2つの単位面積当りの表面力を取り扱う.したがって,破壊条件としては合力で与えられる式を直接利用する.すなわち,FEMではテンソル量としての応力から主応力などを利用して破壊条件式を考えるの対し,RBSMではベクトル量としての合力によって破壊条件を表す.
一方,
HPMでは,RBSMと同様,小領域境界辺上における法線方向及びせん断方向に関する2つの単位面積当りの表面力を取り扱うとともに,小領域内において,FEMと同じテンソル量としての応力を扱うことができる.したがって,領域間の破壊条件と領域内の破壊条件の2種類の破壊条件を用いて,材料非線形解析を行うことが可能となる.両者の破壊を同時に取り扱うためには,それぞれに対して破壊条件を設定する必要がある.
(1)ペナルティ関数に対する破壊基準
はじめに,領域間の破壊条件について述べる.HPMでは,ペナルティ関数にすべりなどの条件を考慮して領域境界面でのすべりを表現し,離散化極限解析を行う.この場合,ベクトル量としての表面力を取り扱うことになるため,構成則や非線形解析法の考え方は,RBSMの場合とほとんど変わらない.いま,要素間の表面力を
式(2.4)のように $\boldsymbol{\lambda}=\left( \lambda_n , \lambda_s \right)$ で表す.このとき,代表的な
降伏関数 $f$ を求めてみよう.
(Trescaの条件)
図3.1(a)に示されているように,Trescaの条件ではせん断方向の表面力 $\lambda_s$ が垂直方向の表面力 $\lambda_n$ に関係なく,せん断強度 $c$ を越えたら破壊するものと考える.
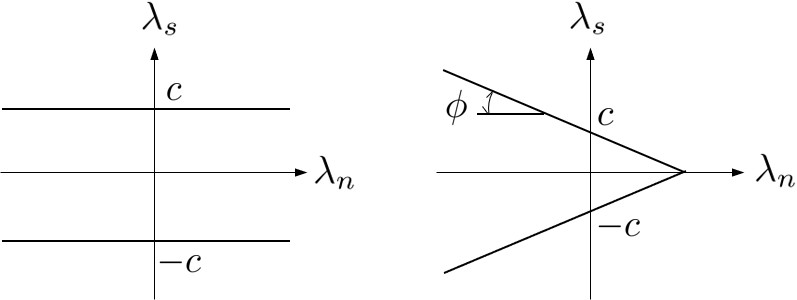
$\hspace{1em}$(a)Trescaの条件
$\hspace{3em}$(b)Mohr-Coulombの条件
$\hspace{5em}$図3.1 すべりに関する降伏条件
この関係を式で表すと,降伏関数を $f$ として以下のようになる.
\[
{\rm (3.1)}
\left.
\begin{array}{l}
\lambda_s = \pm c \\
f = \lambda_s^2 - c^2
\end{array}
\right\}
\]
(Mohr-Coulombの条件)
Mohr-Coulombの条件は
図3.1(b)に示すように,せん断方向の表面力 $\lambda_s$ が垂直方向の表面力 $\lambda_n$ の1次関数となっている場合で,内部摩擦角を $\phi$ としたとき以下のように与えられる.
\[
{\rm (3.2)}
\left.
\begin{array}{l}
\lambda_s = \pm ( c - \tan \phi \cdot \lambda_n) \\
f = \lambda_s^2 - (c-\tan \phi \cdot \lambda_n)^2
\end{array}
\right\}
\]
ただし,
式(3.2)では引つ張り方向の法線方向表面力を正と考えている.
(vonMisesの条件)
図3.2はvonMisesの条件を示した図である.
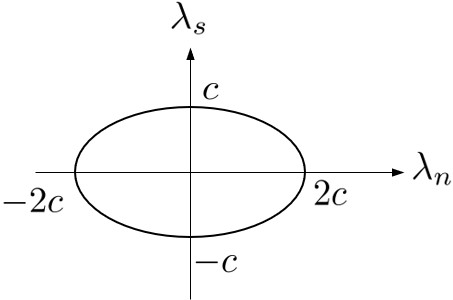
$\hspace{1em}$図3.2 vonMisesの降伏条件
ここに,$c$ はせん断降伏応力である.この場合の降伏関数 $f$ は以下のようになる.
\[
{\rm (3.3)}
\left.
\begin{array}{l}
\displaystyle \lambda_s^2 + \frac{1}{4} \lambda_n^2 = c^2 \\
\displaystyle f = \lambda_s^2 + \frac{1}{4}\lambda_n^2 - c^2
\end{array}
\right\}
\]
(2)要素内における破壊基準
次に,要素内の破壊条件について述べる.HPMで取り扱う要素内応力は,FEMの要素内応力と同じ,テンソル量で表される物理量となる.したがって,降伏関数の記述は,FEMの場合と全く同様に行えばよい.この点に関しては,多くの書籍も出版されているので,ここでは,2次元問題に対する代表的な破壊条件を紹介するにとどめる.
(vonMisesの降伏条件)
\[
{\rm (3.4)}
\sqrt{3}
\left( J_2 \right)^{1/2}
=
\sigma_Y
\]
(Trescaの降伏条件)
\[
{\rm (3.5)}
2 \left(
J_2
\right)^{1/2}
\cos \theta
=
\sigma_Y
\]
(Mohr-Coulombの降伏条件)
\[
{\rm (3.6)}
\frac{1}{3}
I_1 \sin \phi
+
\left(
J_2
\right)^{1/2}
\left(
\cos \theta
-
\frac{1}{\sqrt{3}} \sin \theta \sin \phi
\right)
=
c \cos \phi
\]
(Drucker-Pragerの降伏条件
\[
{\rm (3.7)}
\alpha I_1
+
\left(
J_2
\right)^{1/2}
=
k'
\]
\[\hspace{5em}
\alpha
=
\frac{2 \sin \phi}{\sqrt{3}(3-\sin \phi)}
\;\;,\;\;
k'
=
\frac{6c \sin \phi}{\sqrt{3}(3-\sin \phi)}
\]
ここで,$\sigma_Y$ は降伏応力,$\phi$ は内部摩擦角,$c$ はせん断強度(粘着力)で,$\theta$ はLode角である.$I_1$ と $I_2$ は応力不変量で,2次元問題の場合,以下の関係にある.
(平面ひずみ)
\[
{\rm (3.8)}
I_1
=
\sigma_x + \sigma_y + \sigma_z
=
\sigma_1 + \sigma_2 + \sigma_3
\]
\[
{\rm (3.9)}
I_2
=
\sigma_x \sigma_y
+ \sigma_y \sigma_z
+ \sigma_z \sigma_x
- \tau_{xy}^2
=
\sigma_1 \sigma_2
+ \sigma_2 \sigma_3
+ \sigma_3 \sigma_1
\]
(平面応力)
\[
{\rm (3.10)}
I_1
=
\sigma_x + \sigma_y
=
\sigma_1 + \sigma_2
\]
\[
{\rm (3.11)}
I_2
=
\sigma_x \sigma_y
- \tau_{xy}^2
=
\sigma_1 \sigma_2
\]
また,$J_2$ は,偏差応力の応力不変量で,以下のとおりである.
\[
{\rm (3.12)}
J_2
=
-\left(
\frac{1}{3} I_1^2 - I_2
\right)
\]
RBSMでは,法線及びせん断に関する表面力は2種類のばねを通して隣接要素に伝わる.一旦,このばねの受け持つ力が前節で示した降伏条件に達するとすべりなどの破壊が発生し,その後,破壊条件を満足しながら表面力が増加,減少する.一方,HPMでは,小領域間の変位の連続性に関する付帯条件をLagrangeの未定乗数を用いて導入しており,この未定乗数が表面力を意味するということから,RBSMのばねと同様なモデル化を行っている.したがって,ペナルティ関数を非常に硬いばねととらえれば,RBSMにおけるばねと同様にすべり破壊を取り扱うことができる.本節ではこのような小領域間におけるすべりなどの破壊現象を表現するための構成式について説明する.
いま,領域間の表面力を
式(2.4)のように $\boldsymbol{\lambda}=\left( \lambda_n , \lambda_s \right)$ で表す.このとき,
3.1節で説明した降伏関数 $f$は,以下のように一般的に表すことができる.
\[
{\rm (3.13)}
f( \boldsymbol{\lambda} ) = 0
\]
一方,塑性ポテンシャル $Q$ についても同様に
\[
{\rm (3.14)}
Q( \boldsymbol{\lambda} ) = 0
\]
とする.一般的な塑性流れ則は応力とひずみの関係で表されているが,HPMでは,RBSMと同様,ひずみの代わりに相対変位 $\boldsymbol{\delta}=\left( \delta_n , \delta_s \right)$ を,また,応力の代わりに表面力を用いている.そこで,塑性化後の相対変位の増分 $\Delta \boldsymbol{\delta}^{\; p}$ を以下のように考える.
\[
{\rm (3.15)}
\Delta \boldsymbol{\delta}^{\; p}
=
\mu \frac{\partial Q}{\partial \boldsymbol{\lambda}}
\]
ここで,$\Delta$ は増分量であることを,また,上付の $p$ は塑性状態の量を示している.塑性化する前の量を上付の $e$ で表せば,全相対変位は以下のようになる.
\[
{\rm (3.16)}
\Delta \boldsymbol{\delta}^{\; e}
=
\Delta \boldsymbol{\delta}
-
\Delta \boldsymbol{\delta}^{\; p}
\]
一方,塑性化前の表面力と相対変位の関係は
\[
{\rm (3.17)}
\boldsymbol{\lambda}
=
\boldsymbol{k}^e
\cdot
\boldsymbol{\delta}^e
\]
であり,増分表面力 $\Delta \boldsymbol{\lambda}$ は次のように表せる.
\[
{\rm (3.18)}
\Delta \boldsymbol{\lambda}
=
\Delta \boldsymbol{k}^e
\left(
\Delta \boldsymbol{\delta}
-
\mu
\frac{\partial Q}
{\partial \boldsymbol{\lambda}}
\right)
\]
さらに,塑性条件
\[
{\rm (3.19)}
\frac{\partial f}
{\partial \boldsymbol{\lambda}}
\Delta \boldsymbol{\lambda}
=
0
\]
に代入し,$\mu$ について解くと以下の関係が得られる.
\[
{\rm (3.20)}
\mu
=
\frac{
\displaystyle
\boldsymbol{k}^e \frac{\partial f}{\partial \boldsymbol{\lambda}}
}
{
\displaystyle
\frac{\partial f}{\partial \boldsymbol{\lambda}}
\boldsymbol{k}^e
\frac{\partial Q}{\partial \boldsymbol{\lambda}}
}
\Delta \boldsymbol{\delta}
\]
塑性状態において,
式(3.20)で示される $\mu$ 値が負になったとき,除荷状態になり,除荷状態で $\mu$ の値が正になったとき再負荷状態になる.
(塑性状態)$\mu \lt 0$ → 除荷状態
(除荷状態)$\mu \gt 0$ → 再負荷状態
以上の関係を整理すれば,塑性化後の小領域境界に関する増分表面力と増分相対変位の関係が以下のように得られる.
\[
{\rm (3.21)}
\Delta \boldsymbol{\lambda} =
\left(
\boldsymbol{k}^e -
\frac{
\displaystyle
\boldsymbol{k}^e \frac{\partial f}{\partial \boldsymbol{\lambda}}
\frac{\partial Q}{\partial \boldsymbol{\lambda}}
\boldsymbol{k}^e
}
{
\displaystyle
\frac{\partial f}{\partial \boldsymbol{\lambda}}
\boldsymbol{k}^e
\frac{\partial Q}{\partial \boldsymbol{\lambda}}
}
\right)
\Delta \boldsymbol{\delta}
\]
上式において,$f \equiv Q$ であれば,
関連流れ則に従うことになる.
式(3.21)における ( ) 内の第2項を $\boldsymbol{k}^{p}$ とし,関連流れ則を仮定して各種破壊条件に対する塑性化後の構成行列を求める.
(Mohr-Coulombの条件)
式(3.2)で表される2次元状態における要素間のすべり破壊に対するMohr-Coulombの条件の場合,$\boldsymbol{k}^{p}$ は以下のようになる.
\[
{\rm (3.22)}
\boldsymbol{k}^{p}
=
\frac{1}{F}
\left[
\begin{array}{cc}
k_n^2\{(c-\lambda_n \tan \phi) \tan \phi \}^2 &
k_n k_s \lambda_s ( c - \lambda_n \tan \phi) \tan \phi) \\
{\rm sym.} & k_s^2 \lambda_s^2
\end{array}
\right]
\]
ここで,$c$ は粘着力,$\phi$ は内部摩擦角で,Trescaの条件の場合は $\phi=0$ とする.ただし,
\[\hspace{5em}
F
=
k_s \lambda_s^2
+
k_n \{(c-\lambda_n \tan \phi) \tan \phi \}^2
\]
除荷,再負荷の値は
式(3.20)で表される $\mu$ 値を用いて行う.2次元状態におけるMohr-Coulombの条件についてこの値を求めると以下のようになる.
\[
{\rm (3.23)}
\mu
=
\frac{1}{2F}
\left\{
k_s \cdot
\lambda_s \cdot
\Delta \delta_s
+
k_n (c- \lambda_n \tan \phi)
\tan \phi \cdot \Delta \delta_n
\right\}
\]
(vonMisesの条件)
要素間のすべり破壊に対するvonMisesの条件は,
式(3.3)のように表すことができる.このとき,
式(3.21) に示す は以下のようになる.
\[
{\rm (3.24)}
\boldsymbol{k}^{p}
=
\frac{1}{F}
\left[
\begin{array}{cc}
\frac{1}{4} k_n^2 \lambda_n^2 &
k_n k_s \lambda_s \lambda_n \\
{\rm sym.} & 4 k_s^2 \lambda_s^2
\end{array}
\right]
\]
ただし,
\[\hspace{5em}
F
=
\frac{k_n}{4} \lambda_n^2
+
4 k_s \lambda_s^2
\]
除荷,再負荷の値は,Mohr-Coulombの条件と同様,
式(3.20)で表される $\mu$ 値を用いて行う.vonMisesの条件についてこの値を求めると以下のようになる.
\[
{\rm (3.25)}
\mu
=
\frac{1}{F}
\left(
k_n \frac{\lambda_n}{2} \Delta \delta_n
+
2 k_s \lambda_s \Delta \delta_{st}
\right)
\]
HPMでは,小領域(要素)内の剛体変位とひずみが自由度となっており,ハイブリッド型仮想仕事式に小領域の変形特性が考慮されている.この取り扱いは,通常の有限要素法と同様で,破壊条件および構成則の表現方法は,連続体力学に基づく有限要素解析で用いられている方法と同じである.本節では,vonMisesの条件,Trescaの条件,Mohr-Coulombの条件,Drucker-Pragerの条件の四つの条件について説明する.
はじめに,小領域内の降伏について説明する.ここで述べる方法は,従来の有限要素法で用いられている方法と同じ方法である.いま,小領域内の応力を $\boldsymbol{\sigma}$ で表す.このとき,降伏関数 $g$ は以下のように表すことができる.
\[
{\rm (3.26)}
g(\boldsymbol{\sigma}) = 0
\]
一方,塑性ポテンシャル $\Phi$についても同様に,
\[
{\rm (3.27)}
\Phi (\boldsymbol{\sigma}) = 0
\]
とする.このとき,塑性化後のひずみ増分 $ \Delta \boldsymbol{\varepsilon}^p $ を以下のように考える.
\[
{\rm (3.28)}
\Delta \boldsymbol{\varepsilon}^p
=
\eta
\frac{\partial \Phi}{\partial \boldsymbol{\sigma}}
\]
ここで,$\Delta$ は増分量であることを,また,上付の $p$ は塑性状態の量を示している.塑性化する前の量を上付の $e$ で表せば,全ひずみは以下のようになる.
\[
{\rm (3.29)}
\Delta \boldsymbol{\varepsilon}^e
=
\Delta \boldsymbol{\varepsilon}
-
\Delta \boldsymbol{\varepsilon}^p
\]
一方,塑性化前の応力-ひずみ関係は,
\[
{\rm (3.30)}
\boldsymbol{\sigma}
=
\boldsymbol{D}^e
\cdot
\boldsymbol{\varepsilon}^e
\]
であり,増分応力 $\Delta \boldsymbol{\sigma}$ は次のように表すことができる.
\[
{\rm (3.31)}
\Delta \boldsymbol{\sigma}
=
\Delta \boldsymbol{D}^e
\left(
\Delta \boldsymbol{\varepsilon}
-
\eta
\frac{\partial \Phi}{\partial \boldsymbol{\sigma}}
\right)
\]
さらに,塑性条件
\[
{\rm (3.32)}
\frac{\partial g}{\partial \boldsymbol{\sigma}}
\Delta \boldsymbol{\sigma}
= 0
\]
に代入し,$\eta$ について解くと以下の関係が得られる.
\[
{\rm (3.33)}
\eta
=
\frac{
\displaystyle
\boldsymbol{D}^e \frac{\partial g}{\partial \boldsymbol{\sigma}}
}
{
\displaystyle
\frac{\partial g}{\partial \boldsymbol{\sigma}}
\boldsymbol{D}^e
\frac{\partial \Phi}{\partial \boldsymbol{\sigma}}
}
\Delta \boldsymbol{\varepsilon}
\]
塑性状態において,
式(3.33)で示される $\eta$ 値が負になったとき,除荷状態になり,除荷状態で $\eta$ 値が正になったとき再負荷状態になる.
(塑性状態)$\eta \lt 0$ → 除荷状態
(除荷状態)$\eta \gt 0$ → 再負荷状態
以上の関係を整理すれば,塑性化後の小領域に関する増分応力 $\Delta \boldsymbol{\sigma}$ と増分ひずみ $\Delta \boldsymbol{\varepsilon}$ の関係が以下のように得られる.
\[
{\rm (3.34)}
\Delta \boldsymbol{\sigma}
=
\left(
\boldsymbol{D}^e
-
\frac{\boldsymbol{D}^e
\displaystyle\frac{\partial g}{\partial \boldsymbol{\sigma}}
\displaystyle\frac{\partial \Phi}{\partial \boldsymbol{\sigma}}
\boldsymbol{D}^e }
{ \displaystyle\frac{\partial g}{\partial \boldsymbol{\sigma}}
\boldsymbol{D}^e
\displaystyle\frac{\partial \Phi}{\partial \boldsymbol{\sigma}} }
\right)
\Delta \boldsymbol{\varepsilon}
\]
上式において,$g \equiv \Phi$ であれば,関連流れ則に従うことになる.いま,
式(3.34)を簡単に次のように書く.
\[
{\rm (3.35)}
\Delta \boldsymbol{\sigma}
=
\left(
\boldsymbol{D}^e - \boldsymbol{D}^p
\right)
\Delta \boldsymbol{\varepsilon}
\]
このとき,
\[
{\rm (3.36)}
\boldsymbol{D}^{p}
=
\frac{\boldsymbol{d}
\boldsymbol{d}^T
}
{
\boldsymbol{d}^T
\boldsymbol{\alpha}
}
\]
\[
{\rm (3.37)}
\boldsymbol{d}
=
\boldsymbol{D}^e
\boldsymbol{\alpha}
\]
\[
{\rm (3.38)}
\boldsymbol{\alpha}
=
C_1 \boldsymbol{\alpha}_1
+
C_2 \boldsymbol{\alpha}_2
+
C_3 \boldsymbol{\alpha}_3
\]
\[\hspace{5em}
C_1 = \frac{\partial g}{\partial I_1}
\]
\[\hspace{5em}
C_2 =
\left(
\frac{\partial g}{\partial (J_2)^{1/2}}
-
\frac{\tan 3 \theta}{(J_2)^{1/2}}
\frac{\partial g}{\partial \theta}
\right)
\]
\[\hspace{5em}
C_3 =
\frac{- \sqrt{3}}{2 \cos 3 \theta}
\frac{1}{(J_2)^{3/2}}
\frac{\partial g}{\partial \theta}
\]
ここで,$I_1, I_2, I_3$ は,応力不変量,$J_1, J_2, J_3$ は,偏差応力の応力不変量である.また,$\theta$ は以下に示すようなLode角である.
\[
{\rm (3.39)}
\sin 3 \theta
=
\frac{3 \sqrt{3}}{2}
\frac{J_3}{(J_2)^{3/2}}
\]
\[\hspace{5em}
\sin 3 \theta \gt 1
\;\; {\rm then} \;\;
\sin 3 \theta = 1
\]
\[\hspace{5em}
\sin 3 \theta \lt -1
\;\; {\rm then} \;\;
\sin 3 \theta = -1
\]
\[\hspace{5em}
J_2 = 0
\;\; {\rm then} \;\;
\sin 3 \theta = 0
\]
いま,
式(3.4)から
式(3.7)で表される,vonMisesの条件,Trescaの条件,Mohr-Coulombの条件,Drucker-Pragerの条件に対する
式(3.38)の係数 $C_1 , C_2, C_3$ を整理すると
表3.1 のように表される.
表3.1 係数$C_1, C_2, C_3$
| 降伏基準 |
$C_1$ |
$C_2$ |
$C_3$ |
|---|
| vonMisesの条件 |
0 |
$\sqrt{3}$ |
0 |
| Trescaの条件 |
0 |
$2 (\cos \theta 1+\tan \theta \tan 3 \theta)$ |
$\displaystyle\frac{\sqrt{3}}{J_2} \frac{\sin \theta}{\cos 3 \theta}$ |
| Mohr-Coulombの条件 |
$\frac{1}{3} \sin \phi$ |
$\cos \theta [( 1 + \tan \theta \tan 3 \theta
+\sin \phi ( \tan 3 \theta - \tan \theta)/\sqrt{3}]$ |
$\displaystyle\frac{\sqrt{3}}{J_2} \frac{\sin \theta}{\cos 3 \theta}$ |
| Drucker-Pragerの条件 |
$\alpha$ |
1 |
0 |
ただし,Trescaの条件とMohr-Coulombの条件に関しては,$\theta = \pm30^o$ において,以下の値となる.
(Trescaの条件)
\[
{\rm (3.40)}
C_1 = 0 \;,\;
C_2 = \sqrt{3} \;,\;
C_3 = 0
\]
(Mohr-Coulombの条件)
\[
{\rm (3.41)}
C_1 = \frac{1}{3} \sin \phi \;,\;
C_2 = \frac{1}{2}
\left(
\sqrt{3} - \frac{\sin \phi}{\sqrt{3}}
\right) \;,\;
C_3 = 0
\]
また,$\boldsymbol{\alpha}_1 \;,\; \boldsymbol{\alpha}_2 \;,\; \boldsymbol{\alpha}_3$ は,それぞれの応力状態に応じて以下のようになる.
(平面ひずみ)
\[
\boldsymbol{\alpha}_1^t = \lfloor 1 \;,\; 1 \;,\; 0 \;,\; 1 \rfloor
\]
\[
\boldsymbol{\alpha}_2^t =
\frac{1}{2(J_2)^{1/2}}
\lfloor S_{xx} \;,\; S_{yy} \;,\ 2 \tau_{xy} \;,\; S_{zz} \rfloor
\]
\[
\boldsymbol{\alpha}_3^t =
\lfloor
S_{yy} S_{zz} + \frac{J_2}{3}
\;,\;
S_{xx} S_{zz} + \frac{J_2}{3}
\;,\;
-2 S_{zz} \tau_{xy}^2
\;,\;
S_{xx} S_{yy} -\tau_{xy}^2 + \frac{J_2}{3}
\rfloor
\]
(平面応力)
\[
\boldsymbol{\alpha}_1^t =
\lfloor 1 \;,\; 1 \;,\; 0 \;,\; 0 \rfloor
\]
\[
\boldsymbol{\alpha}_2^t =
\frac{1}{2(J_2)^{1/2}}
\lfloor S_{xx} \;,\; S_{yy} \;,\ 2 \tau_{xy} \;,\; 0 \rfloor
\]
\[
\boldsymbol{\alpha}_3^t =
\lfloor
S_{yy} S_{zz} + \frac{J_2}{3}
\;,\;
S_{xx} S_{zz} + \frac{J_2}{3}
\;,\;
-2 S_{zz} \tau_{xy}^2
\;,\;
0
\rfloor
\]
ここで,$S_{xx}, S_{yy}, S_{zz}$ は偏差応力を表している.
降伏の判定には,それぞれ,
表3.2の単軸状態の降伏応力を用いて以下のような相当応力で行う.
表3.2 降伏判定のための相当応力と等価降伏応力
| 降伏基準 |
応力レベル(相当応力) |
単軸(等価降伏応力) |
|---|
| vonMisesの条件 |
$\sqrt{3} ( J_2)^{1/2}$ |
$\sigma_Y$ |
| Trescaの条件 |
$2 (J_2)^{1/2} \cos \theta$ |
$\sigma_Y$ |
| Mohr-Coulombの条件 |
$\frac{1}{3} I_1 \sin \phi + (J_2)^{1/2}$
$\times( \cos \theta - \sin \theta \sin \phi/\sqrt{3})$
|
$c \cos \phi$ |
| Drucker-Pragerの条件 |
$\alpha I_1 + (J_2)^{1/2}$ |
$k'$ |
式(3.37)に示す $\boldsymbol{d}$ の計算において,平面問題の場合,以下の関係を用いる.
(平面ひずみ)
\[
{\rm (3.42)}
\boldsymbol{D}^e
=
\frac{E(1-\nu)}{(1+\nu)(1-2\nu)}
\left[
\matrix{
1 & \frac{\nu}{1-\nu} & 0 & \frac{\nu}{1-\nu} \cr
\frac{\nu}{1-\nu} & 1 & 0 & \frac{\nu}{1-\nu} \cr
0 & 0 & \frac{1-2\nu}{2(1-\nu)} & 0 \cr
\frac{\nu}{1-\nu} & \frac{\nu}{1-\nu} & 0 & 1
}
\right]
\]
(平面応力)
\[
{\rm (3.43)}
\boldsymbol{D}^e
=
\frac{E}{1-\nu^2}
\left[
\matrix{
1 & \nu & 0 & 0 \cr
\nu & 1 & 0 & 0 \cr
0 & 0 & \frac{1-\nu}{2} & 0 \cr
0 & 0 & 0 & 0
}
\right]
\]
なお,
式(3.42)(3.43)は,$\boldsymbol{d}$ を求めるだけに使われる関係で,通常の要素剛性行列を計算するために使われるものではない.
要素境界面のすべりや降伏を追跡する非線形解析法として,山田らによる
荷重増分法における ${\rm r_{min}}$
法がある.この方法によれば,順次破壊の進展を追跡することができるが,引張破壊などのように応力解放が伴う場合,その解放力によってさらに破壊が進展し,計算が収束しにくくなるという問題点がある.この問題に対して,竹内らは${\rm r_{min}}$ 法を応力解放が伴う問題に対して適用できるように拡張し,HPMの非線形解析に適用した.この方法は,小領域境界辺の破壊に対する手法であるが,本節ではこれをさらに拡張し小領域内での破壊も容易に考慮することができる非線形解析法について説明する.
いま,表面力の降伏関数を $f$,小領域内応力の降伏関数を $g$,現在の表面力と小領域内応力を,それぞれ,$\boldsymbol{\lambda}$,$\boldsymbol{\sigma}$ とし,増分表面力,増分小領域内応力を $\Delta \boldsymbol{\lambda}$,$\Delta \boldsymbol{\sigma}$ とするとき,次式を満たす $r$ が存在する.
\[
{\rm (3.44)}
f( \boldsymbol{\lambda} + r \cdot \Delta \boldsymbol{\lambda} ) \le 0
\]
\[
{\rm (3.45)}
g( \boldsymbol{\sigma} + r \cdot \Delta \boldsymbol{\sigma} ) \le 0
\]
この $r$ を
荷重増分率と呼び,これを考えている様々な表面力,小領域内応力に基づく破壊条件に対して求める.

$\hspace{0em}$(a)表面力に対する荷重増分率
$\hspace{2em}$(b)応力に対する荷重増分率
$\hspace{5em}$図3.3 ${\rm r_{min}}$ 法における荷重増分率の関係
例えば,
図3.3(a) に示すように,現在の点Pと増分後の仮の点Rの区間において,表面力は線形的に変化するものと考え,表面力が降伏曲面上の点Qになるために必要な荷重増分率 $r$ を
\[
{\rm (3.46)}
r = \frac{PQ}{PR}
\]
として求める.これをすべての降伏していない境界辺の表面力に対して計算する.同様に,
図(b)に示す小領域内応力に対する荷重増分率も
式(3.46)を用いて求める.このようにして求まった増分率のうち,最小のものを今回の荷重増分率とする.このとき,現在の値と増分後の値を,それぞれ $n$ と $n+1$ をつけて表すと,
\[
{\rm (3.47)}
\boldsymbol{\lambda}^{n+1} =
\boldsymbol{\lambda}^n + r \cdot \Delta \boldsymbol{\lambda}
\]
\[
{\rm (3.48)}
\boldsymbol{\sigma}^{n+1} =
\boldsymbol{\sigma}^n + r \cdot \Delta \boldsymbol{\sigma}
\]
として増分後の値が求まる.この結果,増分後の表面力,小領域内応力は,降伏曲面を越えることはなく,降伏曲面上もしくはその内側に必ずあることになる.
非線形解析にあたり,荷重 $\boldsymbol{P}$ を幾つかの増分荷重 $\Delta \boldsymbol{P}$ に分割する.このとき,ある荷重増分段階における現在の荷重を $\Delta \boldsymbol{P}^{(i)}$ とし,荷重増分率を $r_{i}$ とすれば,残りの荷重 $\Delta \boldsymbol{P}^{(i+1)}$ は次式によって与えられる.
\[
{\rm (3.49)}
\Delta \boldsymbol{P}^{(i+1)}
=
(1-r_i) \Delta \boldsymbol{P}^{(i)}
\]
したがって,第 $n$ ステップ目の残りの増分荷重は,始めに与えた増分荷重を $\Delta \boldsymbol{P}$ として以下のようになる.
\[
{\rm (3.50)}
\Delta \boldsymbol{P}^{(n)}
=
\prod_{i=0}^{n-1}
\left[
(1-r_i)
\right]
\Delta \boldsymbol{P}
\;\;\; ( r_0 = 0)
\]
いま,$k-1$ 回目で,ある境界に引張破壊が発生した場合,その境界におけるペナルティ関数の値を $0$ として力の伝達を遮断し,その境界において所有していた表面力を解放力 $\Delta \boldsymbol{F}^{(k-1)}$ として,関連小領域に分配する.分配された解放力は,次式のように,残りの荷重に加え,次のステップにおける増分計算を行う.
\[
{\rm (3.51)}
\Delta \boldsymbol{P}^{(n)} =
\prod_{i=0}^{n-1} \left[ (1-r_i) \right] \Delta \boldsymbol{P}
+
\sum_{k=1}^{n}
\left(
\prod_{i=k}^{n} \left[ (1-r_i) \right] \Delta \boldsymbol{F}^{(k-1)}
\right)
\]
このようにして,初めに与えた荷重と解放力をすべて使い切るまで繰り返し計算を行う.このとき,荷重増分率の合計を
\[
{\rm (3.52)}
r_{_{TOTAL}} =
\sum_{k=1}^n \left(
\prod_{i=0}^{k-1} \left[ (1-r_i) \right]
\right) r_k
\]
とし,$r_{TOTAL}=1$ で収束したものと考えることができる.
以上示したように,本アルゴリズムは,解放力を与えること以外は従来の荷重増分法における ${\rm r_{min}}$ 法と同様なアルゴリズムとなっており,小領域内降伏も容易に取り扱うことができる.次に,代表的な破壊条件に対する荷重増分率の求め方について説明する.
(1)ペナルティ関数に対する荷重増分率
(Mohr-Coulombの条件における荷重増分率)
\[
{\rm (3.53)}
(\lambda_s + r \cdot \Delta \lambda_s)^2
\le
\{ c - (\lambda_n + r \cdot \Delta \lambda_n) \tan \phi \}^2
\]
より,次の2次方程式を解くことによって求めることができる.
\[
{\rm (3.54)}
A \cdot r^2 + B \cdot r + c = 0
\]
\[\hspace{6em}
A = \Delta \lambda_s^2 - (\Delta \lambda_n \tan \phi)^2
\]
\[\hspace{6em}
B = 2 \{\lambda_s \Delta \lambda_s - (c-\lambda_n \tan \phi) \Delta \lambda_n \tan \phi \}
\]
\[\hspace{6em}
C = \lambda_s^2 - (c - \lambda_n \tan \phi)^2
\]
(vonMisesの条件における荷重増分率)
\[
{\rm (3.55)}
(\lambda_s + r \cdot \Delta \lambda_s)^2
+
\frac{1}{4} (\lambda_n + r \cdot \Delta \lambda_n)^2
\le c
\]
この場合の
式(3.54)に示す2次方程式の係数は以下のようになる
\[\hspace{6em}
A = \frac{1}{4} \Delta \lambda_n^2 + \Delta \lambda_s^2
\]
\[\hspace{6em}
B = \frac{1}{2} \lambda_n \Delta \lambda_n
+ 2 \lambda_s \cdot \Delta \lambda_s
\]
\[\hspace{6em}
C = \frac{1}{4} \lambda_n^2 + \lambda_s^2 - c^2
\]
(2)小領域の降伏に対する荷重増分率
荷重増分率は
式(3.46)によって求める.いま,
表3.2に示すように,現在の応力レベル(相当応力)を $\sigma_{eq}$,増分の応力レベルを $\Delta \sigma_{eq}$ さらに等価降伏応力を $\sigma'_Y$ とするとき,
式(3.46)の関係は以下のようになる.
\[
{\rm (3.56)}
r = \frac{\sigma'_Y- \sigma_{eq}}{\Delta \sigma_{eq}}
\]
ここで,代表的な破壊条件に対する応力レベル $\sigma_{eq}$ と等価降伏応力 $\sigma'_Y$ の関係を
表3.3 に示す.
表3.3 荷重増分率のための応力レベルと等価降伏応力
| 降伏基準 |
応力レベル $\sigma_{eq}$ |
等価降伏応力 $\sigma'_Y$ |
|---|
| vonMisesの条件 |
$\sqrt{3} ( J_2)^{1/2}$ |
$\sigma_Y$ |
| Trescaの条件 |
$2 (J_2)^{1/2} \cos \theta$ |
$\sigma_Y$ |
| Mohr-Coulombの条件 |
$\frac{1}{3} I_1 \sin \phi + (J_2)^{1/2}$
$\times( \cos \theta - \sin \theta \sin \phi/\sqrt{3})$
|
$c \cos \phi$ |
| Drucker-Pragerの条件 |
$\alpha I_1 + (J_2)^{1/2}$ |
$k'$ |


