４．離散化解析の入力データ


４－１　入力データ種類

 本節では，HPMによる離散化解析に必要となる入力データを整理する．自由度設定位置の関係から，基本的なRBSMによる離散化極限解析の場合と同じデータ構造を有している．一方で，小領域の変形を取り扱うため，FEMと同様のデータも必要である．以下，代表的なHPMのデータ構造について述べる．
（１）座標データ
 FEMやRBSMと同様，HPMにおいても解析領域を有限な小領域に分割し，この小領域を利用して離散化解析を行う．したがって，それらの小領域の形状を認識するため，小領域を構成している節点の座標を入力する必要がある．HPMの場合もBSMと同様，節点に自由度を設けるわけではないので，FEMにおける節点の使われ方とは異なるが，単にデータ構造としてこの節点データを捕らえた場合，FEMと全く同じと考えてよい．
 
$\hspace{5em}$図4.1　節点座標
 以上のように，HPMにおいても節点における $x$ 座標，$y$ 座標をFEMと同様に入力しなければならない．
（２）小領域（要素）データ
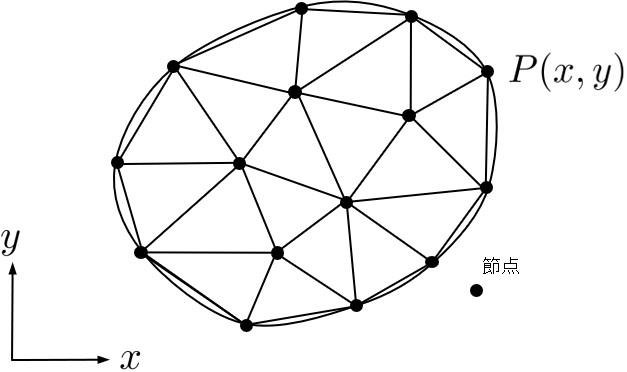
 小領域の形状を認識するためには，各小領域がどの節点から構成されているか，小領域を構成している節点番号を入力する必要がある．小領域形状が 図4.2(a) のように三角形の場合にはFEMにおける定ひずみ要素のデータ構造と全く同じになる．
 
$\hspace{2em}$(a) 三角形要素 $\hspace{3em}$(b) n角形要素 $\hspace{2em}$(c) 境界用要素
$\hspace{7em}$図4.2　要素構成節点番号の読み方
 しかし，HPMでは，RBSMと同様，図(b)に示すようなn角形要素も可能である．また，RBSMの場合，図(c)のような境界や載荷面に用いる境界用要素を使用することがあるが，HPMでも同様に，境界用の要素を用いることができる．しかし，一般的には，境界用の要素を使用せず，ペナルティ関数を用いて，境界辺や節点を拘束する方法が用いられる．このようにモデル化すると，小領域（要素）データを作成する段階ではFEMのデータ構造と同じになる．
（３）材料データ
 HPMでは，FEMと同様，小領域内の変形特性を評価するため，弾性係数やポアソン比といった，変形に関わる材料定数を入力する必要がある．また，領域内の塑性などの材料非線形を扱う必要があれば，強度定数などもFEMと同様に指定する．一方，領域間の強度定数については，RBSMと同様に垂線を重みとして2要素間の平均的な強度定数を用いるか，直接ばねに強度定数を指定する．例えば，断層などの不連続面の強度指定を行う場合が直接指定する場合に該当する．
（４）境界条件データ
 2.5節で述べたように，HPMでは，直接自由度を拘束せず，該当点あるいは辺の変位を小領域の変位場を用いて計算し，その変位をペナルティ関数により近似的に拘束するのが一般的である．本書のサンプル・プログラムでもこの方法を用いている．したがって，HPMにおける拘束条件に関するデータとしては，変位場を指定するための小領域番号と，拘束位置，すなわち，節番号や辺番号を指定する必要がある．強制変位を扱うのであれば，強制変位量も合わせて指定する必要がある．
（５）荷重データ
 FEMでは，通常，自由度位置である節点に荷重を作用させる．要素境界辺に分布荷重を作用させる場合も，実際は，等価節点力として節点に荷重を作用させている．また，RBSMでも，節点ではないが，自由度設定位置に荷重を作用させている．一方，HPMでも，自由度設定位置に荷重を作用させるため，RBSMと同様に小領域番号（要素番号）を指定し，直接自由度位置に荷重を作用させる方法も考えられる．しかし，一般的には，拘束条件と同様，荷重も節点や要素境界辺に作用させ，自由度設定値の外力に換算して計算を行う．したがって，入力情報も，拘束条件と同様，荷重を作用させる小領域の番号とその位置（節点番号や辺番号）とすることが一般的である．
（６）ペナルティデータ
 RBSMでは2要素間の相対変位を利用してばね剛性行列を誘導しており，このためには，各要素境界辺を共有する要素番号や節点番号を認識しておかなければならない．一方，HPMでも，ペナルティ行列を誘導するにあたり，RBSMと同様，2要素間の相対変位を利用する．したがって，RBSMと同様，各小領域境界辺を共有する小領域の番号や節点番号を認識しておかなければならない．しかし，このデータは要素データを基にプログラム内部で作成可能なデータであるため，入力の必要は無い．なお，FEMにおけるジョイント要素のように接触面や不違続面の表現に使用する場合は，ばね定数を直接入力する必要が生じる．
（７）図心データ
 RBSMでは要素内の任意位置（一般には図心位置）に自由度を設定する．HPMも，RBSMと同様に，小領域内の任意位置に自由度を設定するが，便宜上，その位置を図心に設定するのが一般的である．このデータはプログラム内部で作成することができるため，部分的にパラメータ設定位置を変えたい場合以外は，入力の必要はない．
（８）垂線データ
 RBSMでは仮想ひずみなどを計算する場合，垂線を用いて求めるため，必ず必要となるデータである．一方，HPMでは，仮想ひずみのような物理量を計算する上で垂線を利用することはない．ただし，ペナルティ関数の重みとして垂線を利用する場合や，ペナルティ関数の強度を求める際に小領域で指定した定数の平均値を求める場合などで利用することがある．しかし，よほど特別な理由がない限りプログラム内部で作成するため，入力することはない．
 HPMによる離散化解析におけるデータ処理部の簡単なプログラムフローを図4.3に示す．図に示すように，基本データの入力後，解析に必要となるペナルティデータや図心，垂線なその幾何情報を作成する．
 
$\hspace{6em}$図4.3　入力部のフロー
 データの入力プログラムは付録のリスト160行～255行に掲載されているサブルーチン(InputData)である．読者なりの書式に変更したい場合にはこのサブルーチンを差し替えればよい．図4.3に従い入力部のフローをプログラム化したものがプログラム4.1である．
 プログラム4.1　データ作成コントロール(Prepocessing) 

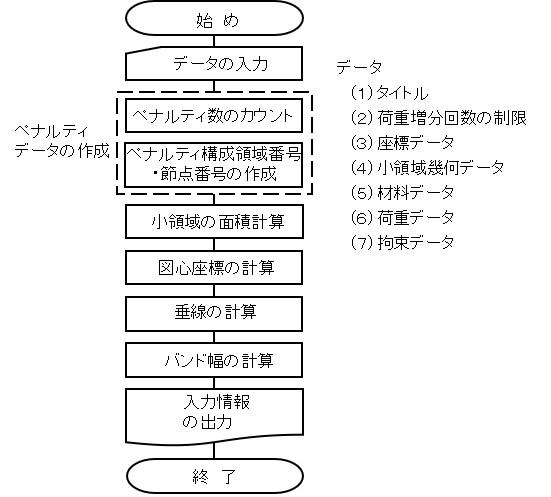
134	!==========================================================================
135	  SUBROUTINE Prepocessing( Title, Node, Element, Material, Spring, Load, &
136	                           Boundary, Nonlinear, Solver, File)
137	
138	    CHARACTER*80,       INTENT(OUT) :: Title    
139	    TYPE(typeNode),     INTENT(OUT) :: Node     
140	    TYPE(typeElement),  INTENT(OUT) :: Element  
141	    TYPE(typeMaterial), INTENT(OUT) :: Material 
142	    TYPE(typeSpring),   INTENT(OUT) :: Spring   
143	    TYPE(typeLoad),     INTENT(OUT) :: Load     
144	    TYPE(typeBoundary), INTENT(OUT) :: Boundary 
145	    TYPE(typeNonLinear),INTENT(OUT) :: NonLinear
146	    TYPE(typeBand),     INTENT(OUT) :: Solver   
147	    TYPE(typeFile),     INTENT(IN)  :: File     
148	
149	    CALL InputData(Title,Node,Element,Material,Load,Boundary, &
                           Nonlinear,Solver,File)
150	    Spring%no = noSpring(Element) 
151	    CALL SpringData(Element,Spring)
152	    CALL Area(Node,Element)
153	    CALL gCenter(Node,Element)
154	    CALL Perpendicular(Node,Element,Spring)
155	    Solver%width = BandWidth(Element,Spring)
156	    CALL PrintData(Title,Node,Element,Material,Spring,Load,Boundary, &
157	                   Nonlinear,Solver,File)
158	  END SUBROUTINE Prepocessing
 関数(noSpring)およびサブルーチン(SpringData)でばねデータが作成される．このことについては次節においてさらに詳しく述べることにする．
 サブルーチン(Area)は三角形の要素面積を計算するためのプログラムで，FEMでも利用されているおりここでは説明を省略する．ただし，373行（付録参照）にあるIF文で境界用要素を識別し，もし境界用の要素であれば面積を0としている．本書に掲載したサンプル・プログラムでは，境界用要素の取り扱いができないため，このIF文は削除可能である．

４－２　ペナルティデータの作成

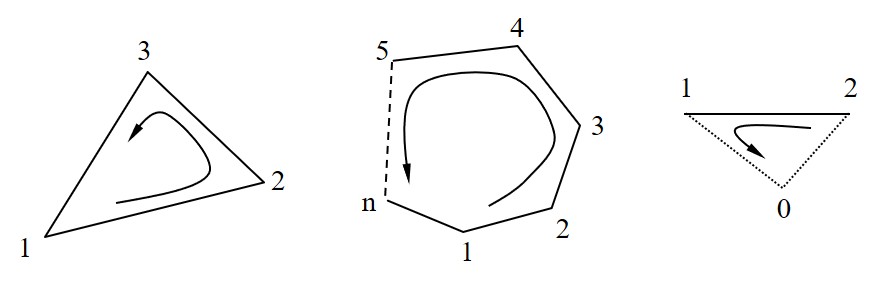
 先にも述べたようにFEMと異なるデータの一つとして，変位の連続性を指定するペナルティ関数の設定位置に対するデータがあげられる．このデータを手作業で入力することは，当然のこととして手間がかかるし，入力ミスを誘い易いため，できるだけプログラム内部で作成したほうがよい．本書に掲載したサンプル・プログラムでは，このようなペナルティデータの作成を2つのプログラムにより行つている．
 一つは関数(noSpring)で，このプログラムではペナルティ関数を設定する小領域境界辺の数をカウントしている．よほど特殊な場合でないかぎり，一つのペナルティ関数を設定する辺は2つの小領域のみ共有する．プログラム4.2はその例である．273行において2つの要素が共有する節点数を(same)という変数により調べ，この値が2のときばねが存在すると考える．もし，この値が3であれば，それは2つの要素が全く同じ要素構成節点番号を持つていることになり，明らかに小領域構成節点データにミスがある．また，1 以下の場合はデータのミスではなく，共有する要素境界辺が存在していないことを意味する．
 プログラム4.2　ペナルティ数のカウント(noSpring) 

256	!--------------------------------------------------------------------------
257	  FUNCTION noSpring( Element ) RESULT( no )
258	
259	    TYPE(typeElement), INTENT(IN) :: Element
260	    INTEGER :: no,ie,je,same,edge,error,i,j
261	
262	    no    = 0
263	    error = 0
264	
265	    DO ie = 1, Element%no - 1
266	      edge = 0
267	      DO je = ie+1, Element%no
268	        same = 0
269	        DO i = 1, 3
270	          IF(Element%node(i,ie) /= 0) THEN
271	            DO j = 1, 3
272	              IF(Element%node(i,ie) == Element%node(j,je)) THEN
273	                same = same + 1
274	              END IF
275	            END DO
276	          END IF
277	        END DO
278	        IF(same > 2) THEN
279	          error = error + 1
280	          PRINT 6000, ie,je
281	          6000 FORMAT(/,' *** ERROR *** SAME NODE  ELEM. NO.(',I3,',',I3,')')
282	         ELSE IF(same == 2) THEN
283	          no = no + 1
284	          edge = edge + 1
285	        END IF
286	      END DO
287	      IF(edge > 3) THEN
288	        error = error + 1
289	        PRINT 6010, ie,(Element%node(i,ie),i=1,3)
290	        6010 FORMAT(/,' *** ERROR *** NODE DATA  ELEM. NO.',I3, &
291	                      '  NODE NO.(',I3,',',I3,',',I3,')')
292	      END IF
293	    END DO
294	    IF(error == 0) RETURN
295	    STOP 100
296	  END FUNCTION noSpring
 サンプルプログラムでは三角形形状のみを考えている．したがって，一つの領域において，領域境界辺は3以下でなければならない．このことを図に示したものが図4.4である．図に示すように，三角形形状のみ利用する場合はペナルティ関数を設定する位置（以後，ペナルティ辺と呼ぶ）として，(a)(b)(c)の3ケースが考えられる．もし，3以上の境界辺があつたなら，それは明かにデータに誤りがあることになる．なお，本プログラムではペナルティ辺の数（以後，ペナルティ数と呼ぶ）を(Spring%no)という変数により表現している．
 
$\hspace{4em}$(a) $\hspace{9em}$(b) $\hspace{10em}$(c)
$\hspace{6em}$図4.4　ある領域が共有する境界辺のタイプ
 ペナルティ辺は，小領域境界辺を共有する2つの領域番号とその辺を構成する節点番号で特定する．前者のデータは(Spring%element)という配列に，後者のデータは，(Spring%node)という配列に格納している．これらの作業はプログラム4.3に示すサブルーチン(SpringData)により行つている．2次元問題の場合，ペナルティ構成節点数は2である．ここで，注意をしなければいけないことは図4.5に示すように，ペナルティ構成節点番号における順番がペナルティ構成領域番号の1番目の小領域に支配されていることである．すなわち，(Spring%element)に格納された1番目の小領域に着目し，その領域からみ見て反時計回りにペナルティ構成節点番号を作成しなければならない．その理由は，相対変位や表面力を計算する場合に使用する，領域境界辺上に設けた法線方向をこの配列(Spring%node)から決定するためである．このように考えておけば，得られる表面力は引つ張りが正，圧縮が負となる．
 
$\hspace{5em}$図4.5　ペナルティ構成節点番号の考え方
 プログラム4.3　ペナルティデータ(SpringData)
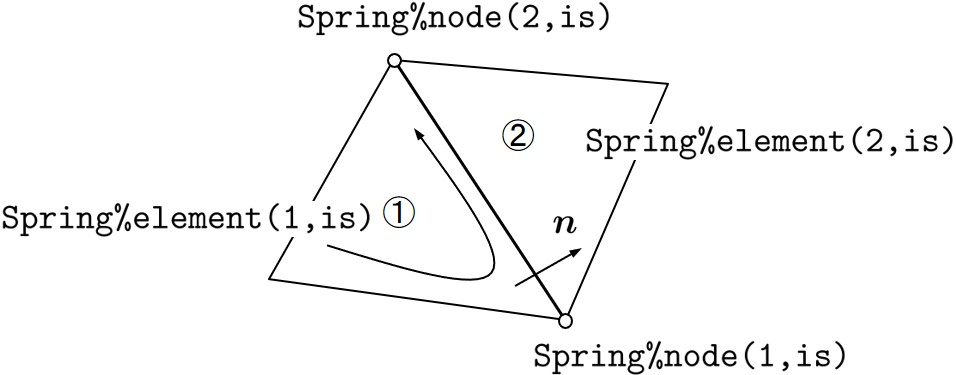
$\hspace{8em}$（ペナルティ構成領域・節点番号の作成） 

297	!--------------------------------------------------------------------------
298	  SUBROUTINE SpringData( Element, Spring ) 
299	
300	    TYPE(typeElement),  INTENT(IN)    :: Element
301	    TYPE(typeSpring),   INTENT(INOUT) :: Spring 
302	    INTEGER :: no,is,ie,je,in,jn,n1,n2,same,i,j,ibit
303	
304	    ALLOCATE( Spring%node(2,Spring%no) )
305	    ALLOCATE( Spring%element(2,Spring%no) )
306	    ALLOCATE( Spring%length(Spring%no) )
307	    ALLOCATE( Spring%hline(2,Spring%no) )
308	    ALLOCATE( Spring%flag(Spring%no) )
309	    ALLOCATE( Spring%strain(2,Spring%no,Line%no) )
310	    ALLOCATE( Spring%dstrain(2,Spring%no,Line%no) )
311	    ALLOCATE( Spring%stress(2,Spring%no) )
312	    ALLOCATE( Spring%dstress(2,Spring%no) )
313	
314	    no = 0
315	
316	    DO ie = 1, Element%no - 1
317	      DO je = ie+1, Element%no
318	        same = 0
319	        DO i = 1, 3
320	          IF(Element%node(i,ie) /= 0) THEN
321	            DO j = 1, 3
322	              IF(Element%node(i,ie) == Element%node(j,je)) THEN
323	                same = same + 1
324	              END IF
325	            END DO
326	          END IF
327	        END DO
328	        IF(same == 2) THEN
329	          no = no + 1
330	          Spring%element(1,no) = ie
331	          Spring%element(2,no) = je
332	        END IF
333	      END DO
334	    END DO
335	    Loop : DO is = 1, Spring%no
336	      ie = Spring%element(1,is)
337	      je = Spring%element(2,is)
338	      DO i = 1, 3
339	        in = Element%node(i,ie)
340	        ibit = 0
341	        DO j = 1, 3
342	          jn = Element%node(j,je)
343	          IF(in == jn) THEN
344	            ibit = 1
345	          END IF
346	        END DO
347	        IF(ibit == 0) THEN
348	          n1 = i + 1
349	          n2 = i + 2
350	          IF(n1 > 3) n1 = n1 - 3
351	          IF(n2 > 3) n2 = n2 - 3
352	          Spring%node(1,is) = Element%node(n1,ie)
353	          Spring%node(2,is) = Element%node(n2,ie)
354	          CYCLE Loop
355	        END IF
356	      END DO
357	    END DO Loop
358	  END SUBROUTINE SpringData
 本書に掲載したペナルティデータ発生プログラムは参考例であり，必要に応じて読者なりのプログラムを開発してもよい．ただし，先に示したペナルティ構成節点番号の付け方に対しては十分な注意が必要である．

４－３　図心の計算

 FEMでは各節点に自由度を設定するため，座標データとして節点の座標値を読み込むことで 必然的に自由度の位置が入力されたのと同じことになる． しかし，HPMでは小領域（要素）内の任意の位置に自由度を設定するため， その位置を指定しておかなければならない．本書ではその位置を図心にとっている．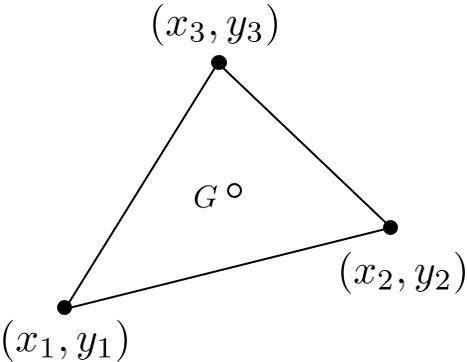
 
$\hspace{3em}$図4.6　図心の計算
 領域形状が図4.6に示すような三角形の場合，以下のように計算することができる． \[ {\rm (4.1)}   x_{_G} = \frac{x_1+x_2+x_3}{3}  ,  y_{_G} = \frac{y_1+y_2+y_3}{3} \]
 プログラム4.4は，図心を計算するプログラムである．なお，本プログラムでは，407行の判定文により境界用の要素にも対応できるようコード化されている．
 プログラム4.4　図心座標の計算(gCenter) 

349	!--------------------------------------------------------------------------
394	  SUBROUTINE gCenter( Node, Element )
395	
396	    TYPE(typeNode),     INTENT(IN)    :: Node   
397	    TYPE(typeElement),  INTENT(INOUT) :: Element
398	    INTEGER :: ie,n,i
399	    REAL(8) :: ww,wx,wy
400	
401	    DO ie = 1, Element%no
402	      ww = 0.0
403	      wx = 0.0
404	      wy = 0.0
405	      DO i = 1, 3
406	        n = Element%node(i,ie)
407	        IF(n /= 0) THEN
408	          ww = ww + 1
409	          wx = wx + Node%coord(1,n)
410	          wy = wy + Node%coord(2,n)
411	        END IF
412	      END DO
413	      Element%center(1,ie) = wx/ww
414	      Element%center(2,ie) = wy/ww
415	    END DO
416	  END SUBROUTINE gCenter

４－４　垂線の計算

 RBSMではばね定数を決定するため，垂線を利用している．一方，HPMでは，垂線を用いなくても良いが，2.2節で述べたように，重みとして利用することが多い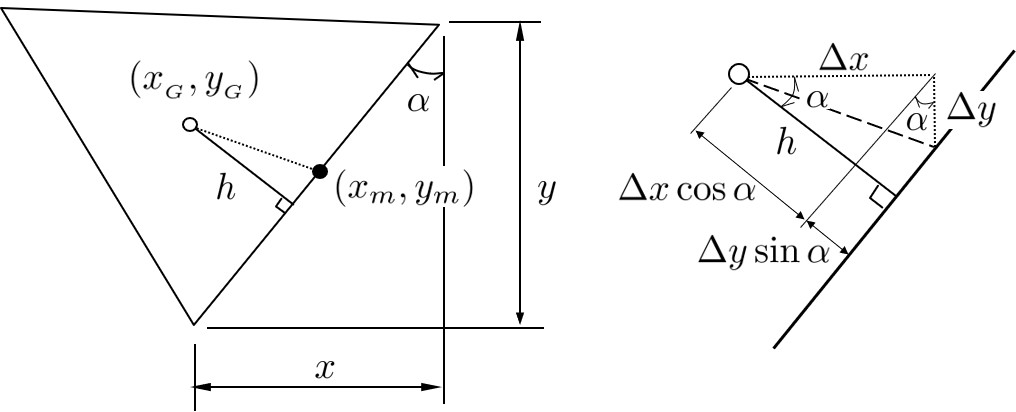．図4.7はこの計算過程を図化したものである．
 
$\hspace{10em}$図4.7　垂線の計算
 垂線は1つの領域境界辺に対して2つの領域が関係しているため，各領域境界辺に対し領域①側と領域②側の2つを計算しなければならない．はじめに領域境界辺の傾きを以下の式により求める．
\[ {\rm (4.2)}   l = \cos \alpha = \frac{x}{L}  ,  m = \sin \alpha = \frac{y}{L} \]
次に，要素図心の座標 $\left( x_{_G}, y_{_G} \right)$ から要素境界辺上の中点 $\left( x_{_m}, y_{_m} \right)$ に結んだ線 $\overline{\rm GM}$ の $x$ 方向成分，$y$ 方向成分を
\[ {\rm (4.3)}   \Delta x = x_{_m} - x_{_G}  ,  \Delta y = y_{_m} - y_{_G} \]
のごとく計算し，この成分をさらに法線方向へ座標変換することによって垂線を以下のように計算することができる．
\[ {\rm (4.4)}   h = \Delta x \cdot m - \Delta y \cdot l \]
 これをプログラム化したものがプログラム4.5のサブルーチン(Perpendicular)である．変数(Spring%hline)には垂線の値が記憶されており，438行～440行で①要素側の垂線 $h_1$ を計算し，441行～443行で②要素側の垂線 $h_2$ を計算している．
 プログラム4.5　垂線の計算(Perpendicular) 

417	!--------------------------------------------------------------------------
418	  SUBROUTINE Perpendicular( Node, Element, Spring ) 
419	
420	    TYPE(typeNode),    INTENT(IN)    :: Node   
421	    TYPE(typeElement), INTENT(IN)    :: Element
422	    TYPE(typeSpring),  INTENT(INOUT) :: Spring 
423	    INTEGER :: is,n1,n2,e1,e2
424	    REAL(8) :: sl,sm,xm,ym,h1,h2,x,y,xl,yl
425	
426	    DO is = 1, Spring%no
427	      n1 = Spring%node(1,is)
428	      n2 = Spring%node(2,is)
429	      x  = Node%coord(1,n2) - Node%coord(1,n1)
430	      y  = Node%coord(2,n2) - Node%coord(2,n1)
431	      Spring%length(is) = DSQRT(x*x+y*y)
432	      sl = y/Spring%length(is)
433	      sm = x/Spring%length(is)
434	      xm = (Node%coord(1,n1) + Node%coord(1,n2)) /2.D0
435	      ym = (Node%coord(2,n1) + Node%coord(2,n2)) /2.D0
436	      e1 = Spring%element(1,is)
437	      e2 = Spring%element(2,is)
438	      xl = xm - Element%center(1,e1)
439	      yl = ym - Element%center(2,e1)
440	      h1 = sl*xl - sm*yl
441	      xl = Element%center(1,e2) - xm
442	      yl = Element%center(2,e2) - ym
443	      h2 = sl*xl - sm*yl
444	      Spring%hline(1,is) = ABS(h1)
445	      Spring%hline(2,is) = ABS(h2)
446	    END DO
447	  END SUBROUTINE Perpendicular
 本プログラムでは図心に自由度を設定した場合の垂線を計算しているが，図心以外に自由度を設けた場合は配列(Element%center)にその点の座標を入れておけば，そのまま本サブルーチンにより垂線を計算することができる．また，垂線の考え方を変えたい場合はこのサブルーチンを変更すればよい．

４－５　バンド幅の考え方

 本プログラムでは連立方程式の計算に修正コレスキー法を用いたバンド法を利用している．このためには，バンド幅の計算が必要になる．ここでは，このことについて補足しておく．
 
$\hspace{0em}$図4.8　三角形の頂点における節点番号
 三角形の頂点における節点番号を図4.8に示すようにした場合，FEMの定ひずみ要素ではバンド幅は以下のように計算される．
\[ {\rm (4.5)}   バンド幅 = \left\{ {\rm max(n_1,n_2,n_3) - min(n_1,n_2,n_3) } +1 \right\} \times 2 \]
ここで，最後の2は各節点で $(u,v)$ の2自由度を持っているためである．
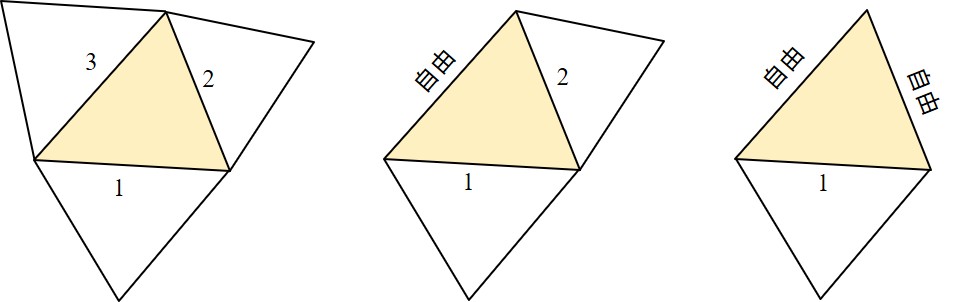
 ところが，HPMでは，節点ではなく要素内の任意の位置に $(u,v,\theta,\varepsilon_x,\varepsilon_y,\gamma_{xy})$ の6自由度を考える．そして，2要素間の境界辺に設けたペナルティ関数により2つの領域を関係付け，ペナルティ係数行列を作成する．したがって，FEMにおける節点に対応するのが領域内に設けた自由度点である．これを図4.9(b)に示すように模式化して考えるとHPMにおけるバンド幅が以下のように計算できる．
\[ {\rm (4.6)}   バンド幅 = \left( \left| {\rm n_1 - n_2} \right| + 1 \right) \times 6 \]
 
$\hspace{2em}$(a) 自由度設定位置 $\hspace{6em}$(b) ばねの自由度素
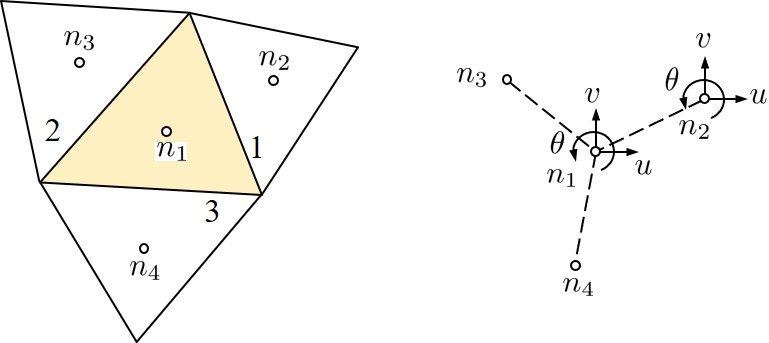
$\hspace{7em}$図4.9　RBSMにおけるバンド幅
ここで，最後の6は各領域の自由度が6であることを意味している．すなわち，ペナルティ辺に関係する2領域の領域番号の差に対する絶対値に対角項分1を加え，その数に各領域の自由度6を掛けたものがバンド幅と定義される．もちろん，系全体のバンド幅を考えるべきであるから，実際のバンド幅は式(4.6)をすべてのペナルティ辺について求め，その内の最大のものとなる．このバンド幅を用いた係数行列の組立については次章において説明を加える．
 以上の関係をプログラム化したものがプログラム4.6の関数(BandWidth)である．ペナルティ辺に関係する領域番号が記憶されている変数(Spring%element)を用いて462行に示すよう，バンド幅を計算する．この計算を全てのペナルティ辺について行い，一番大きな値をもって，その系におけるバンド幅とする．プログラムでは変数(Solver%width)により系全体のバンド幅を定義している．
 プログラム4.6　バンド幅の計算(BandWidth) 

448	!--------------------------------------------------------------------------
449	  FUNCTION BandWidth( Element, Spring ) RESULT( width )
450	
451	    TYPE(typeElement), INTENT(IN) :: Element
452	    TYPE(typeSpring),  INTENT(IN) :: Spring 
453	    INTEGER :: width,is,wd
454	
455	    width = 0
456	    DO is = 1, Spring%no
457	      wd = Spring%element(2,is) - Spring%element(1,is)
458	      IF(wd > width) THEN
459	        width = wd
460	      END IF
461	    END DO
462	    width = (width+1)*Element%dof
463	
464	    ALLOCATE( Solver%stiff(Solver%no*width) )
465	    ALLOCATE( Solver%load(Solver%no) )
466	  END FUNCTION BandWidth