6.離散化解析の応力・表面力計算
6-1 表面力の計算
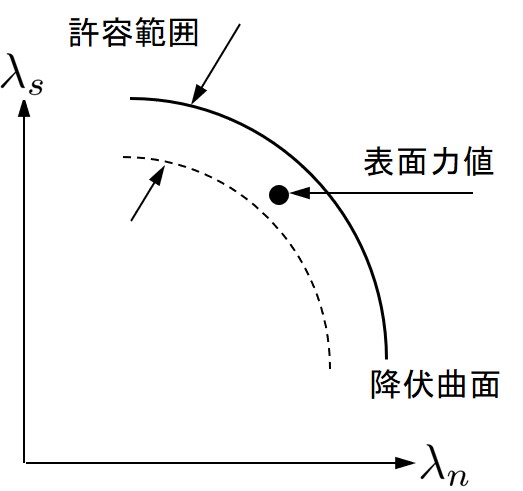
変位型のFEMでは,テンソル量としての要素内応力を求める.一方,HPMでは,FEMと同様,領域内においてテンソル量としての応力が求まるとともに,RBSMと同様,隣接する2領域間の境界辺上における単位面積当りの表面力を求めることができる.本節では,HPMの特徴でもある,表面力を求めるプログラムについて述べる.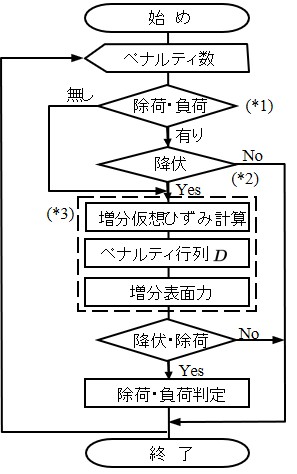
(*1)に示す判定文では増分計算あるいは再計算過程において除荷あるいは負荷が発生したペナルティ辺が存在するか否かのチェックを行つている.もし,一箇所以上のペナルティ辺に除荷もしくは負荷が発生していたなら,以後,降伏しているペナルティ辺についてのみ $\mu$ 計算のための増分計算をおこない,再計算を行う準備を行う.この降伏の判定文が(*2)である.除荷,負荷が発生していなければ通常の(*3)に示す増分計算を行う.
以上の処理は,
1119 !-------------------------------------------------------------------------- 1120 SUBROUTINE SpringStress( Node, Element, Material, Spring, Line, jramc, jramd ) 1121 1122 TYPE(typeNode), INTENT(IN) :: Node 1123 TYPE(typeElement), INTENT(IN) :: Element 1124 TYPE(typeMaterial), INTENT(IN) :: Material 1125 TYPE(typeSpring), INTENT(INOUT) :: Spring 1126 TYPE(typeNumInteg), INTENT(IN) :: Line 1127 INTEGER, INTENT(INOUT) :: jramc 1128 INTEGER, INTENT(INOUT) :: jramd 1129 REAL(8) :: sig(2,3),D(2,2),ww 1130 INTEGER :: is,ip,jbit,i,j 1131 1132 jramd = 0 1133 1134 DO is = 1, Spring%no 1135 IF(jramd == 1 .AND. Spring%flag(is) == 0) CYCLE 1136 IF(jramd == 1 .AND. Spring%flag(is) == -2) CYCLE 1137 CALL Strain(is,Node,Element,Spring,Line ) 1138 CALL formSpring(is,Element,Material,Spring,D) 1139 D = D*Spring%penalty 1140 DO ip = 1, Line%no 1141 DO i = 1, 2 1142 ww = 0.0 1143 DO j = 1, 2 1144 ww = ww + D(i,j)*Spring%dstrain(j,is,ip) 1145 END DO 1146 sig(i,ip) = ww 1147 END DO 1148 END DO 1149 DO i = 1, 2 1150 ww = 0.D0 1151 DO ip = 1, Line%no 1152 ww = ww + sig(i,ip)*Line%weight(ip) 1153 END DO 1154 Spring%Dstress(i,is) = 0.5D0*ww 1155 END DO 1156 IF(jramc .LT. 2) THEN 1157 IF(Spring%flag(is) == 1 .OR. Spring%flag(is) == 2) THEN 1158 jbit = 0 1159 IF(Spring%flag(is) == 2) jbit = 1 1160 CALL Unload(is,Element,Material,Spring,D,jramd,jbit) 1161 END IF 1162 END IF 1163 END DO 1164 jramc = jramc + 1 1165 END SUBROUTINE SpringStress
1056行及び1164行に示す
次に,
一方,1138行では,
この増分表面力 $\Delta \boldsymbol{\lambda}_i$ も,積分点毎の仮想ひずみから求めるため,積分点毎の値となる.この表面力を利用して積分点毎に破壊の判定を行っても良いが,本サンプルプログラムでは応力評価を1点で行い破壊判定をする.そのため,1149行~1155行に示すように,数値積分の重み $w_i$ を用いた重み付き平均によって,以下のように応力を評価している. \[ {\rm (6.1)} \Delta \boldsymbol{\lambda} = \sum_{i=1}^3 \left( w_i \Delta \boldsymbol{\lambda}_i \right) / \sum_{i=1}^3 w_i \] さて,積分点毎の仮想ひずみの計算は \[ {\rm (6.2)} \Delta \boldsymbol{\varepsilon}_i = \frac{1}{h} \boldsymbol{B}_i \cdot \Delta \boldsymbol{u} \] で計算する.ここで,$\Delta \boldsymbol{u}$ はペナルティ辺に関係する隣接領域の自由度を並べたベクトルである.また,$\boldsymbol{B}_i$ は,
1166 !-------------------------------------------------------------------------- 1167 SUBROUTINE Strain( is, Node, Element, Spring, Line ) 1168 1169 INTEGER, INTENT(IN) :: is 1170 TYPE(typeNode), INTENT(IN) :: Node 1171 TYPE(typeElement), INTENT(IN) :: Element 1172 TYPE(typeNumInteg), INTENT(IN) :: Line 1173 TYPE(typeSpring), INTENT(INOUT) :: Spring 1174 REAL(8) :: uu(2*Element%dof),bb(2,2*Element%dof),h,ww 1175 INTEGER :: ie,ip,i,j,ii,jj 1176 1177 ii = 0 1178 DO i = 1, 2 1179 ie = Spring%element(i,is) 1180 DO j = 1, Element%dof 1181 ii = ii + 1 1182 jj = j + (ie-1)*Element%dof 1183 uu(ii) = Element%ddisp(jj) 1184 END DO 1185 END DO 1186 h = Spring%hline(1,is) + Spring%hline(2,is) 1187 DO ip = 1, Line%no 1188 CALL formB(is,ip,Node,Element,Spring,Line,bb) 1189 DO i = 1, 2 1190 ww = 0.D0 1191 DO j = 1, 2*Element%dof 1192 ww = ww + bb(i,j)*uu(j) 1193 END DO 1194 Spring%dstrain(i,is,ip) = ww/h 1195 END DO 1196 END DO 1197 END SUBROUTINE Strain
6-2 除荷・負荷の判定
単位面積当りの表面力を計算する過程において,除荷,負荷の判定が必要であることを前節で述べた.本節ではこのことについて説明する.完全弾塑性体を考えた場合,除荷は
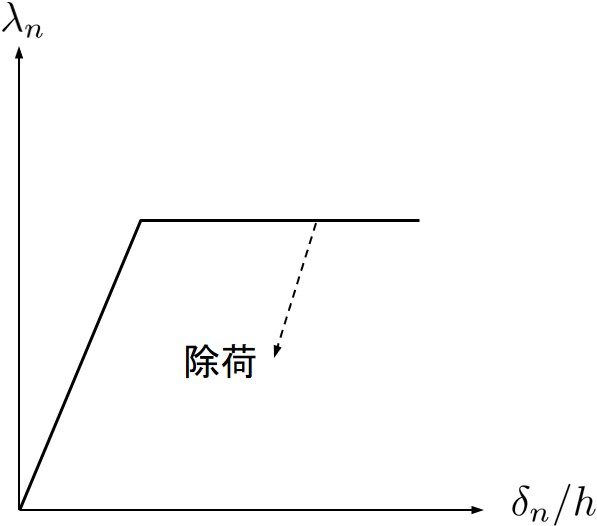
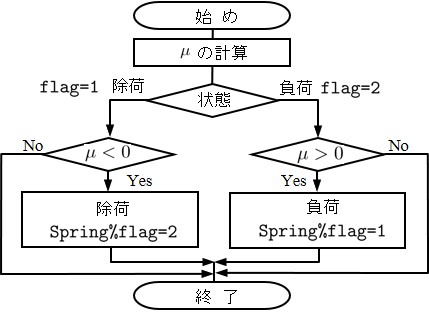
除荷状態 → $\mu \gt 0$ → 負荷発生 → Spring%flag = 1 以上の判定をプログラム化したものが
1198 !-------------------------------------------------------------------------- 1199 SUBROUTINE Unload( is, Element, Material, Spring, D, jramd, jbit) 1200 1201 INTEGER, INTENT(IN) :: is 1202 TYPE(typeElement), INTENT(IN) :: Element 1203 TYPE(typeMaterial), INTENT(IN) :: Material 1204 TYPE(typeSpring), INTENT(INOUT) :: Spring 1205 REAL(8), INTENT(IN) :: D(:,:) 1206 INTEGER, INTENT(INOUT) :: jramd 1207 INTEGER, INTENT(IN) :: jbit 1208 REAL(8) :: lam 1209 1210 lam = Lambda(is,Element,Material,Spring,D) 1211 IF(jbit /= 1) THEN 1212 IF(lam < 0.D0) THEN 1213 Spring%flag(is) = 2 1214 jramd = 1 1215 END IF 1216 ELSE 1217 IF(lam > 0.D0) THEN 1218 Spring%flag(is) = 1 1219 jramd = 1 1220 END IF 1221 END IF 1222 END SUBROUTINE Unload
このサブルーチンに現れる $\mu$ の計算は
Mohr-Coulombの条件の場合,$\mu$ の計算式に強度定数が含まれている.本書のサンプルプログラムでは,この強度定数に対しても垂線を重みとして平均値をとるよう考えている.この平均値の計算は1223 !-------------------------------------------------------------------------- 1224 FUNCTION Lambda( is, Element, Material, Spring, D ) RESULT( lam ) 1225 1226 INTEGER, INTENT(IN) :: is 1227 TYPE(typeElement), INTENT(IN) :: Element 1228 TYPE(typeMaterial), INTENT(IN) :: Material 1229 TYPE(typeSpring), INTENT(IN) :: Spring 1230 REAL(8), INTENT(IN) :: D(:,:) 1231 REAL(8) :: lam 1232 REAL(8) :: cm,phi,pt 1233 REAL(8) :: PAI = 3.141592654D0 1234 1235 lam = 0.0 1236 1237 IF(Element%type == 0) THEN 1238 CALL strength(is,Element,Material,Spring,cm,phi) 1239 pt = DTAN(phi*PAI/180.D0) 1240 lam = D(2,2)*Spring%stress(2,is)*Spring%dstrain(2,is,2) & 1241 + D(1,1)*(cm-Spring%stress(1,is)*pt)*pt*Spring%dstrain(1,is,2) 1242 ELSE 1243 lam = 2.0*D(2,2)*Spring%stress(2,is)*Spring%dstrain(2,is,2) & 1244 + 0.5*D(1,1)*Spring%stress(1,is)*Spring%dstrain(1,is,2) 1245 END IF 1246 END FUNCTION Lambda
1265,1266行における1247 !-------------------------------------------------------------------------- 1248 SUBROUTINE strength( is, Element, Material, Spring, cm, phi ) 1249 1250 INTEGER, INTENT(IN) :: is 1251 TYPE(typeElement), INTENT(IN) :: Element 1252 TYPE(typeMaterial), INTENT(IN) :: Material 1253 TYPE(typeSpring), INTENT(IN) :: Spring 1254 REAL(8), INTENT(OUT) :: cm 1255 REAL(8), INTENT(OUT) :: phi 1256 1257 REAL(8) :: h 1258 INTEGER :: ie1,ie2,im1,im2 1259 1260 h = Spring%hline(1,is) + Spring%hline(2,is) 1261 ie1 = Spring%element(1,is) 1262 ie2 = Spring%element(2,is) 1263 im1 = Element%material(ie1) 1264 im2 = Element%material(ie2) 1265 cm = (Material%c(im1)*Spring%hline(1,is) & 1266 + Material%c(im2)*Spring%hline(2,is))/h 1267 phi = (Material%phi(im1)*Spring%hline(1,is) & 1268 + Material%phi(im2)*Spring%hline(2,is))/h 1269 END SUBROUTINE strength
6-3 領域内の応力計算
変位型のFEMでは,節点変位から要素内ひずみを求めた後,このひずみと構成行列から要素内の応力を計算している.一方,HPMにおいても領域内においてテンソル量としての応力を取り扱う.ただし,HPMでは,全体係数行列で示される連立方程式を解くことで,剛体変位とともに,領域内のひずみを直接求める.したがって,領域内の応力は,このひずみから求めることができる.具体的なプログラムを
本サンプルプログラムでは,線形の変位場を用いているため,領域内のひずみは一定となり,したがって,応力も領域内において一定となっている.また,領域内降伏についても,1090 !-------------------------------------------------------------------------- 1091 SUBROUTINE ElementStress( Element, Material ) 1092 1093 TYPE(typeElement), INTENT(IN) :: Element 1094 TYPE(typeMaterial), INTENT(IN) :: Material 1095 REAL(8) :: D(3,3),eps(3),sig(3),ww 1096 INTEGER :: ie,i,j,ii 1097 1098 DO ie = 1, Element%no 1099 IF(Element%node(3,ie) /= 0) THEN 1100 DO i = 1, 3 1101 ii = 3 + i + (ie-1)*Element%dof 1102 eps(i) = Element%ddisp(ii) 1103 END DO 1104 CALL formDmatrix(ie,Element,Material,D) 1105 DO i = 1, 3 1106 ww = 0.D0 1107 DO j = 1, 3 1108 ww = ww + D(i,j)*eps(j) 1109 END DO 1110 sig(i) = ww 1111 END DO 1112 DO i = 1, 3 1113 Element%dstrain(i,ie) = eps(i) 1114 Element%dstress(i,ie) = sig(i) 1115 END DO 1116 END IF 1117 END DO 1118 END SUBROUTINE ElementStress
6-4 拘束箇所の反力計算
HPMの拘束条件の処理方法には,自由度を直接拘束する方法と,ペナルティ関数を用いて間接的に拘束条件と取り込む方法がある.本サンプルプログラムでは,より一般的な処理が可能な後者の方法で拘束条件を導入している.本節では,のような方法で拘束した場合の反力の計算方法について説明する.ペナルティ関数を用いた拘束の方法については,
以上の関係を基に作成したプログラムを
1270 !-------------------------------------------------------------------------- 1271 SUBROUTINE Reaction( Node, Element, Material, Load, Boundary, Line ) 1272 1273 TYPE(typeNode), INTENT(IN) :: Node 1274 TYPE(typeElement), INTENT(IN) :: Element 1275 TYPE(typeMaterial), INTENT(IN) :: Material 1276 TYPE(typeLoad), INTENT(IN) :: Load 1277 TYPE(typeBoundary), INTENT(INOUT) :: Boundary 1278 TYPE(typeNumInteg), INTENT(IN) :: Line 1279 1280 INTEGER :: ib,ie,id,in1,in2,im,in,ip,i 1281 REAL(8) :: f_disp,t,length,shape(2,6),disp(6),uu,reac,wt,pt 1282 1283 pt = Spring%penalty*MAXVAL( Material%young ) 1284 1285 DO ib = 1, Boundary%no 1286 ie = Boundary%element(ib) 1287 id = Boundary%direction(ib) 1288 in1 = Boundary%node(1,ib) 1289 in2 = Boundary%node(2,ib) 1290 f_disp = Boundary%disp(ib) 1291 DO i = 1, Element%dof 1292 in = i + (ie-1)*Element%dof 1293 disp(i) = Element%ddisp(in) 1294 END DO 1295 im = Element%material(ie) 1296 t = Material%thick(im) 1297 length = SQRT((Node%coord(1,in2)-Node%coord(1,in1))**2 & 1298 +(Node%coord(2,in2)-Node%coord(2,in1))**2) 1299 reac = 0.D0 1300 DO ip = 1, 3 1301 CALL formShape(ie,ip,in1,in2,Node,Element,Line,shape) 1302 wt = 0.5*Line%weight(ip)*length*t 1303 uu = 0.D0 1304 DO i = 1, Element%dof 1305 uu = uu + shape(id,i)*disp(i) 1306 END DO 1307 reac = reac + (uu - f_disp)*pt*wt 1308 END DO 1309 Boundary%dreaction(ib) = reac 1310 END DO 1311 END SUBROUTINE Reaction
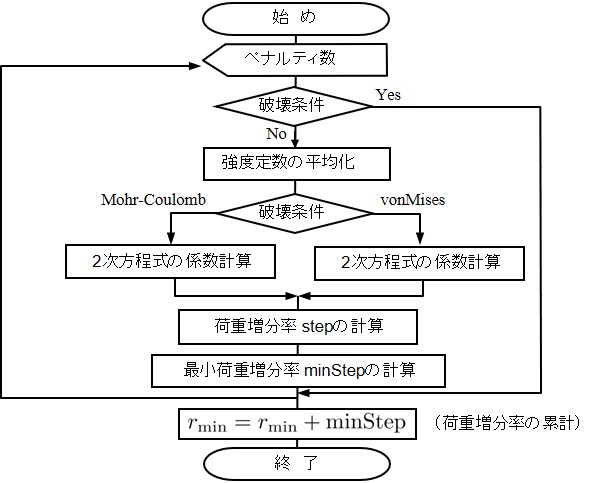
6-5 荷重増分率の計算
荷重増分法における山田の方法により増分計算を行う場合,荷重増分率はプログラム内部で自動的に計算される.本節では,このことについて若干の補足をする.塑性流れ則に従えば,すでに降伏しているペナルティ辺の表面力は,除荷が発生しない限り
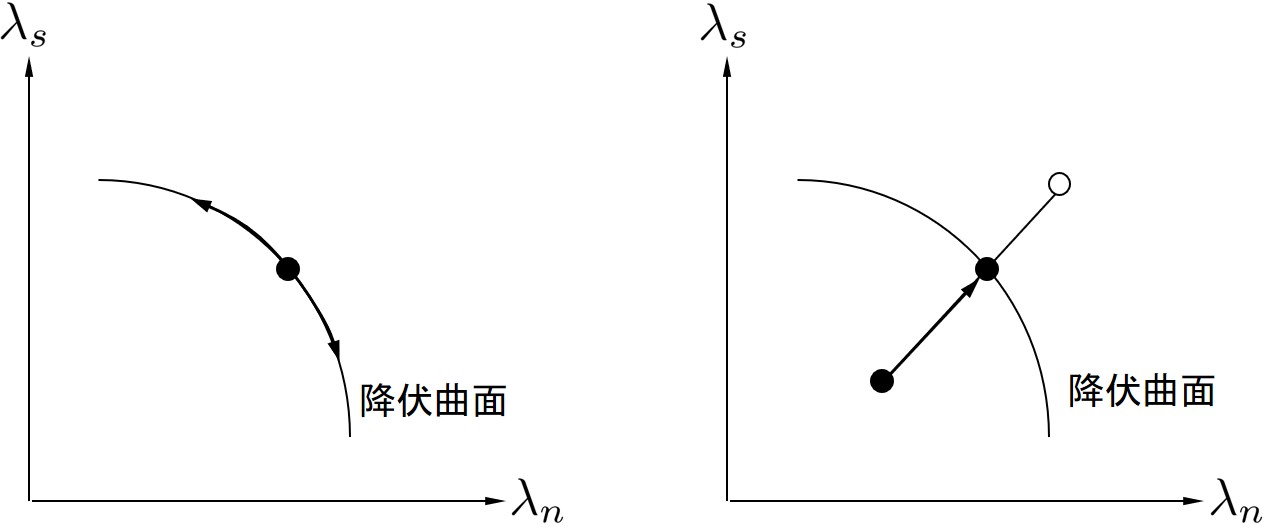
$\hspace{10em}$
これらの関係をプログラム化したものが
2次方程式の根は1312 !-------------------------------------------------------------------------- 1313 SUBROUTINE incRatio( Element, Material, Spring, Nonlinear ) 1314 1315 TYPE(typeElement), INTENT(IN) :: Element 1316 TYPE(typeMaterial), INTENT(IN) :: Material 1317 TYPE(typeSpring), INTENT(IN) :: Spring 1318 TYPE(typeNonLinear),INTENT(INOUT) :: NonLinear 1319 INTEGER :: is 1320 REAL(8) :: minStep,step,cm,phi,pt,a,b,c 1321 REAL(8) :: PAI = 3.141592654D0 1322 1323 minStep = 9999.D0 1324 1325 DO is = 1, Spring%no 1326 CALL strength(is,Element,Material,Spring,cm,phi) 1327 IF(Element%type == 0) THEN 1328 pt = DTAN(phi*PAI/180.D0) 1329 a = Spring%dstress(2,is)**2 - (Spring%dstress(1,is)*pt)**2 1330 b = 2.D0*(Spring%stress(2,is)*Spring%dstress(2,is) & 1331 + (cm-Spring%stress(1,is)*pt)*Spring%dstress(1,is)*pt) 1332 c = Spring%stress(2,is)**2 - (cm-Spring%stress(1,is)*pt)**2 1333 ELSE 1334 a = (Spring%dstress(1,is)**2)/4.D0 + Spring%dstress(2,is)**2 1335 b = Spring%stress(1,is)*Spring%dstress(1,is)/2.D0 & 1336 + 2.D0*Spring%stress(2,is)*Spring%dstress(2,is) 1337 c = (Spring%stress(1,is)**2)/4.D0 + Spring%stress(2,is)**2 & 1338 - cm**2 1339 END IF 1340 step = ratio(a,b,c) 1341 IF(minStep > step) THEN 1342 minStep = step 1343 END IF 1344 END DO 1345 NonLinear%step = minStep 1346 NonLinear%rmin = NonLinear%rmin + minStep 1347 IF(NonLinear%rmin > 0.9998D0) THEN 1348 NonLinear%step = NonLinear%step - NonLinear%rmin + 1.D0 1349 NonLinear%rmin = 1.D0 1350 END IF 1351 END SUBROUTINE incRatio
数値計算では丸め誤差など,各種の誤差が混入するため,厳密に荷重増分率の累計が1.0となることはまれである.そこで1347行に示すよう,倍精度計算の場合,
なお,1340行における
以上のようにして荷重増分率が決定されたなら,今回までの全変位 $\boldsymbol{u}^{n+1}$,全ひずみ $\boldsymbol{\varepsilon}^{n+1}$,および全応力 $\boldsymbol{\sigma}^{n+1}$,全表面力 $\boldsymbol{\lambda}^{n+1}$,全反力 $\boldsymbol{R}^{n+1}$ が以下のように求められる. \[ {\rm (6.6)} \left. \begin{array}{l} \boldsymbol{u}^{n+1} = \boldsymbol{u}^{n} + \Delta \boldsymbol{u}^{n+1} \cdot {\rm step} \\[0.3em] \boldsymbol{\varepsilon}^{n+1} = \boldsymbol{\varepsilon}^{n} + \Delta \boldsymbol{\varepsilon}^{n+1} \cdot {\rm step} \\[0.3em] \boldsymbol{\sigma}^{n+1} = \boldsymbol{\sigma}^{n} + \Delta \boldsymbol{\sigma}^{n+1} \cdot {\rm step} \\[0.3em] \boldsymbol{\lambda}^{n+1} = \boldsymbol{\lambda}^{n} + \Delta \boldsymbol{\lambda}^{n+1} \cdot {\rm step} \\[0.3em] \boldsymbol{R}^{n+1} = \boldsymbol{R}^{n} + \Delta \boldsymbol{R}^{n+1} \cdot {\rm step} \end{array} \right\} \] ここで上付きの(n)が前回までの全変位及び全表面力で(n+1)が今回の量であることを示す.
この関係をもとにプログラム化したものが
本サンプル・プログラムでは,隣接する領域境界に設けられたペナルティ辺の降伏のみ考慮しており,引っ張りに伴うペナルティ辺の切断や,領域内の降伏は無視している.もし,これらの破壊要因を考慮するのであれば,それぞれの破壊要因について,本節で説明した荷重増分率を計算し,それらの中の最小値を荷重増分率とするように設定すればよい.1391 !-------------------------------------------------------------------------- 1392 SUBROUTINE totalValue( Element, Spring, Nonlinear ) 1393 1394 TYPE(typeElement), INTENT(INOUT) :: Element 1395 TYPE(typeSpring), INTENT(INOUT) :: Spring 1396 TYPE(typeNonLinear),INTENT(IN) :: NonLinear 1397 1398 Element%disp = Element%disp + Element%ddisp*NonLinear%step 1399 Element%strain = Element%strain + Element%dstrain*NonLinear%step 1400 Element%stress = Element%stress + Element%dstress*NonLinear%step 1401 Spring%strain = Spring%strain + Spring%dstrain*NonLinear%step 1402 Spring%stress = Spring%stress + Spring%dstress*NonLinear%step 1403 Boundary%reaction = Boundary%reaction + Boundary%dreaction*NonLinear%step 1404 END SUBROUTINE totalValue
6-6 破壊判定
山田の方法を用いた荷重増分計算では増分計算毎に塑性化したペナルティ係数行列や領域内剛性行列を作成し直す.このためには,前回のペナルティ辺や領域内の状態が弾性状態か塑性状態か,あるいは除荷状態か負荷状態かを把握しておく必要がある.本サンプルプログラムでは,ペナルティ辺に関する状態のみ考慮しており,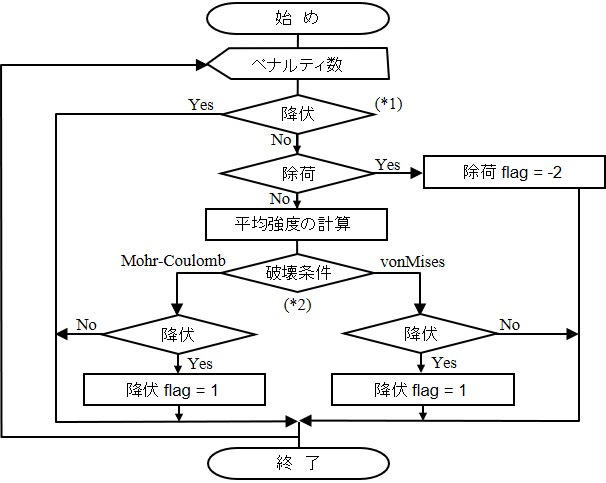
Spring%flag = 1 : 降伏状態
Spring%flag = -2 : 除荷状態 図に示す(*1)の判定は,すでに降伏状態にあるペナルティ辺か否かを判定している.降伏状態にあれば除荷が発生しない限り塑性状態を継続するものとしてフラッグの変更を行わない.もし,ペナルティ辺が降伏状態でなければ除荷状態か否かを判定し,除荷状態であれば以後弾性と見なし,フラッグを
この判定で注意してほしいことはl422行と1429行においてせん断強さに0.998を掛けていることである.厳密にはこのような処理を行う必要はないが,実数計算の場合,丸め誤差等により本来1となるべき解が0.99…となってしまうことが度々ある.前節で説明した全表面力の計算も実数計算であるから,表面力が降伏曲面上に完全に一致することは少ない.1405 !------------------------------------------------------------------------- 1406 SUBROUTINE YieldCheck( Element, Material, Spring ) 1407 1408 TYPE(typeElement), INTENT(IN) :: Element 1409 TYPE(typeMaterial), INTENT(IN) :: Material 1410 TYPE(typeSpring), INTENT(IN) :: Spring 1411 INTEGER :: is 1412 REAL(8) :: cm,phi,pt,tau 1413 REAL(8) :: PAI = 3.141592654D0 1414 1415 DO is = 1, Spring%no 1416 IF(Spring%flag(is) /= 1) THEN 1417 IF(Spring%flag(is) ==2) THEN 1418 Spring%flag(is) = -2 1419 ELSE 1420 CALL strength(is,Element,Material,Spring,cm,phi) 1421 IF(Element%type == 0) THEN 1422 cm = cm*0.998D0 1423 pt = DTAN(phi*PAI/180.0) 1424 tau = ABS(Spring%stress(2,is))+Spring%stress(1,is)*pt 1425 IF(tau > cm) THEN 1426 Spring%flag(is) = 1 1427 END IF 1428 ELSE 1429 cm = cm**2*0.998D0 1430 tau = Spring%stress(1,is)**2/4.D0 + Spring%stress(2,is)**2 1431 IF(tau > cm) THEN 1432 Spring%flag(is) = 1 1433 END IF 1434 END IF 1435 END IF 1436 END IF 1437 END DO 1438 END SUBROUTINE YieldCheck